|
|
ГЛАВА I
Фигуры звезд
В широко распространенном среди астрономов анекдоте рассказывается о том, что на экзамене по теоретической астрофизике студенту достался билет с вопросом о внутреннем строении звезд. Находчивый студент, не зная вопроса, бодро отвечает: " Звезда - это раскаленный газовый шар, а площадь шара равна четыре - пи - эр - квадрат... " и т. д.
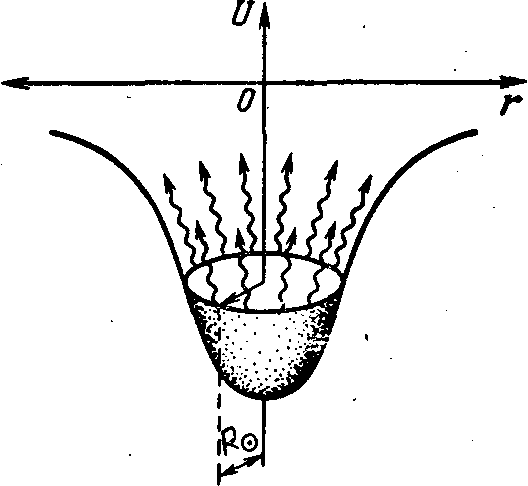
Да, действительно, одиночные звезды имеют форму шара. Почему? Энергетически выгодно. Вещество звезды, подобно жидкости, заполняет сосуд, в который его нали- вают, а поверхность ее совпадает с эквипотенциальной поверхностью. Звезда сама создает поле, в котором ее вещество " разливается " . Мы уже говорили, что потенциал точечной массы изменяется с расстоянием как r-1 (формула (1)), причем в точке г = 0 потенциал уходит в " минус бесконечность " . В природе так не бывает, по крайней мере, в обычных звездах. Потенциал звезды напоминает рюмку с отбитой ножкой (см. рис. 14). При г = 0 потенциал мал, но конечен. На поверхности г = const. т. е. звезда - шар.
А какова форма звезд в двойных системах? Действуя по аналогии с одиночной звездой, мысленно заполним потенциальный рельеф двойной системы (см. рис. 11) жидкостью. Она растечется таким образом, что поверхность звезды будет поверхностью равного потенциала, т. е. поверхностью Хилла.
Звезда вытянется вдоль линии, соединяющей компоненты двойной системы.
Видите, как мы легко расправились с этой проблемой. А в XVIII веке вокруг более простой проблемы разгорелся столь сильный спор, что даже была снаряжена специальная арктическая экспедиция. Эту историю пересказывает выдающийся астрофизик Субраманьян Чандрасекар в своей монографии о фигурах звезд.
В 1687 г. Исаак Ньютон опубликовал свой самый знаенитый труд " Математические начала натуральной философии " . Именно здесь он объяснил кеплеровские законы законом всемирного тяготения, решив и много других "частных" проблем. Одной из них была задача о форме Земли. Ньютон утверждал, что из-за вращения Земля у полюсов сплюснута, и форма ее напоминает репу. Он дал остроумное доказательство этого. Предположив, что в Земле прорыты два колодца до ее центра (см. 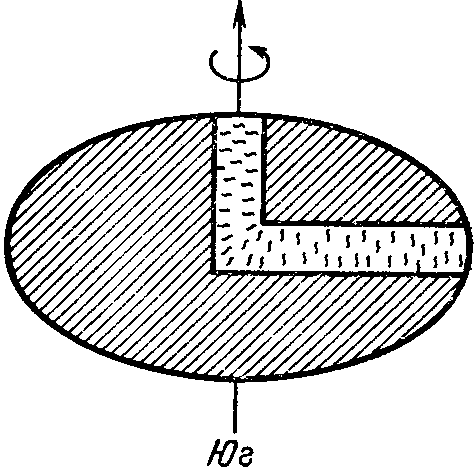рис. 15):
один - вдоль оси вращения, другой - в плоскости экватор;
Колодцы заполнены водой. Дл того чтобы вода находилась равновесии и не выплескивалась, необходимо, чтобы вес жидкости в обоих столбах был одинаковым. Но вес тела - это произведение массы на эффективное ускорение, которое ест разность между ускорением силы тяжести и ускорением центробежных сил. В эквг ториальном колодце ускорение силы тяжести слегк ослабляется центробежным ускорением. Чтобы ве воды на экваторе был таким, как и в полярном колодце уровень воды на экваторе должен быть повыше.
Но этот вывод был в вопиющем противоречии с астрономическими данными того времени! Знаменитый французский астроном Доменико Кассини, проводивший специальные измерения дуги меридиана на территории Франции, считал, что его данные говорят о вытянутости Земли вдоль полюсов. Трудно было не доверять человеку, первому директору Парижской обсерватории, открывшему четыре спутника Сатурна и знаменитую щель в кольцах Сатурна.
