Next: ÐаÑÑдовое ÑопÑÑжение
Up: ÐекÑÐ¸Ñ 3. ÐиÑкÑеÑнÑе ÑиммеÑÑии
Previous: ÐекÑÐ¸Ñ 3. ÐиÑкÑеÑнÑе ÑиммеÑÑии
ÐÑеобÑазование пÑоÑÑÑанÑÑвенного оÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ ÑводиÑÑÑ Ðº
Ð¸Ð·Ð¼ÐµÐ½ÐµÐ½Ð¸Ñ ÑиÑÑÐµÐ¼Ñ ÐºÐ¾Ð¾ÑÐ´Ð¸Ð½Ð°Ñ 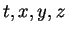 на
на 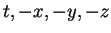 .
ÐÑи Ñаком изменении ÑиÑÑÐµÐ¼Ñ ÐºÐ¾Ð¾ÑÐ´Ð¸Ð½Ð°Ñ ÑазнÑе обÑекÑÑ Ð¿ÑеобÑазÑÑÑÑÑ
по-ÑазномÑ. Так кооÑдинаÑÑ Ð¿Ð¾Ð»ÑÑнÑÑ
векÑоÑов
.
ÐÑи Ñаком изменении ÑиÑÑÐµÐ¼Ñ ÐºÐ¾Ð¾ÑÐ´Ð¸Ð½Ð°Ñ ÑазнÑе обÑекÑÑ Ð¿ÑеобÑазÑÑÑÑÑ
по-ÑазномÑ. Так кооÑдинаÑÑ Ð¿Ð¾Ð»ÑÑнÑÑ
векÑоÑов 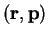 менÑÑÑ
знак, кооÑдинаÑÑ Ð°ÐºÑиалÑнÑÑ
векÑоÑов
менÑÑÑ
знак, кооÑдинаÑÑ Ð°ÐºÑиалÑнÑÑ
векÑоÑов
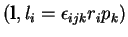 знака не менÑÑÑ. СкалÑÑное пÑоизведение
двÑÑ
полÑÑнÑÑ
векÑоÑов обÑазÑÐµÑ ÑкалÑÑ , не
менÑÑÑийÑÑ Ð¿Ñи пÑоÑÑÑанÑÑвенном оÑÑажении, а
ÑкалÑÑное пÑоизведение полÑÑного и акÑиалÑного векÑоÑа
обÑазÑÐµÑ Ð¿ÑевдоÑкалÑÑ, менÑÑÑий знак пÑи
пÑоÑÑÑанÑÑвенном оÑÑажении. ÐÑоÑÑÑанÑÑвенной ÑеÑноÑÑÑÑ (
знака не менÑÑÑ. СкалÑÑное пÑоизведение
двÑÑ
полÑÑнÑÑ
векÑоÑов обÑазÑÐµÑ ÑкалÑÑ , не
менÑÑÑийÑÑ Ð¿Ñи пÑоÑÑÑанÑÑвенном оÑÑажении, а
ÑкалÑÑное пÑоизведение полÑÑного и акÑиалÑного векÑоÑа
обÑазÑÐµÑ Ð¿ÑевдоÑкалÑÑ, менÑÑÑий знак пÑи
пÑоÑÑÑанÑÑвенном оÑÑажении. ÐÑоÑÑÑанÑÑвенной ÑеÑноÑÑÑÑ (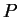 )
какой-либо велиÑÐ¸Ð½Ñ Ð½Ð°Ð·ÑваеÑÑÑ ÐµÐµ ÑвойÑÑво менÑÑÑ Ð¸Ð»Ð¸ не менÑÑÑ
знак пÑи инвеÑÑии пÑоÑÑÑанÑÑвеннÑÑ
кооÑдинаÑ. СкалÑÑ Ð¸ акÑиалÑнÑй
векÑоÑ
)
какой-либо велиÑÐ¸Ð½Ñ Ð½Ð°Ð·ÑваеÑÑÑ ÐµÐµ ÑвойÑÑво менÑÑÑ Ð¸Ð»Ð¸ не менÑÑÑ
знак пÑи инвеÑÑии пÑоÑÑÑанÑÑвеннÑÑ
кооÑдинаÑ. СкалÑÑ Ð¸ акÑиалÑнÑй
векÑÐ¾Ñ 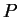 -ÑеÑнÑ, а пÑевдоÑкалÑÑ Ð¸ векÑоÑ
-ÑеÑнÑ, а пÑевдоÑкалÑÑ Ð¸ векÑÐ¾Ñ 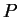 -неÑеÑнÑ.
-неÑеÑнÑ.
Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ð¼Ñ Ð·Ð½Ð°ÐµÐ¼, ÑÑо лагÑанжиан ÑилÑного и ÑлекÑÑомагниÑного
взаимодейÑÑвий не менÑеÑÑÑ Ð¿Ñи пÑоÑÑÑанÑÑвенном оÑÑажении,
Ñ.е. ÑвлÑеÑÑÑ ÑкалÑÑом, а лагÑанжиан Ñлабого взаимодейÑÑвиÑ
ÑвлÑеÑÑÑ ÑÑммой ÑкалÑÑа и пÑевдоÑкалÑÑа.
ÐнваÑианÑноÑÑÑ Ð¾ÑноÑиÑелÑно пÑоÑÑÑанÑÑвенного оÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
кванÑово-меÑ
аниÑеÑком ÑзÑке ознаÑаеÑ, ÑÑо амплиÑÑда пÑоÑеÑÑа и
зеÑкалÑно-ÑиммеÑÑиÑного пÑоÑеÑÑа ÑовпадаÑÑ
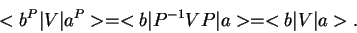
ÐÑли наÑалÑное и конеÑное ÑоÑÑоÑÐ½Ð¸Ñ Ð¸Ð¼ÐµÑÑ Ð¾Ð¿ÑеделеннÑÑ 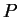 -ÑеÑноÑÑÑ,
-ÑеÑноÑÑÑ,
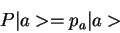
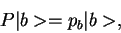
Ñо
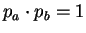 или
или 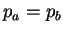 , Ñ.е.
, Ñ.е. 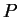 -
ÑеÑноÑÑÑ ÑоÑ
ÑанÑеÑÑÑ.
-
ÑеÑноÑÑÑ ÑоÑ
ÑанÑеÑÑÑ.
ЧеÑноÑÑи ÑаÑÑиÑ
СилÑнÑе и ÑлекÑÑомагниÑнÑе взаимодейÑÑвиÑ, в коÑоÑÑÑ
ÑоÑ
ÑанÑеÑÑÑ
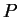 -ÑеÑноÑÑÑ, ÑоÑ
ÑанÑÑÑ Ñакже
-ÑеÑноÑÑÑ, ÑоÑ
ÑанÑÑÑ Ñакже 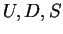 -заÑÑдÑ, Ñ.е. ÑиÑло
-заÑÑдÑ, Ñ.е. ÑиÑло
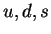 -кваÑков. ÐоÑÑÐ¾Ð¼Ñ ÑеÑноÑÑи
-кваÑков. ÐоÑÑÐ¾Ð¼Ñ ÑеÑноÑÑи 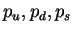 можно ÑÑиÑаÑÑ
пÑоизволÑнÑми. Тогда
можно ÑÑиÑаÑÑ
пÑоизволÑнÑми. Тогда 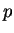 -ÑеÑноÑÑи вÑеÑ
дÑÑгиÑ
ÑоÑÑоÑний бÑдÑÑ
вÑÑажаÑÑÑÑ ÑеÑез ниÑ
. ÐÑинÑÑо ÑÑиÑаÑÑ, ÑÑо
-ÑеÑноÑÑи вÑеÑ
дÑÑгиÑ
ÑоÑÑоÑний бÑдÑÑ
вÑÑажаÑÑÑÑ ÑеÑез ниÑ
. ÐÑинÑÑо ÑÑиÑаÑÑ, ÑÑо
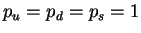 .
Ðдной из ÑеоÑем ÑеоÑии ÑеÑмионов, оÑнованной на ÑÑавнении ÐиÑака,
ÑвлÑеÑÑÑ ÑÑвеÑждение, ÑÑо внÑÑÑенние ÑеÑноÑÑи ÑеÑмиона и
анÑиÑеÑмиона пÑоÑивоположнÑ, Ñ.е.
.
Ðдной из ÑеоÑем ÑеоÑии ÑеÑмионов, оÑнованной на ÑÑавнении ÐиÑака,
ÑвлÑеÑÑÑ ÑÑвеÑждение, ÑÑо внÑÑÑенние ÑеÑноÑÑи ÑеÑмиона и
анÑиÑеÑмиона пÑоÑивоположнÑ, Ñ.е.
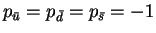 (или
(или
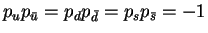 ).
).
ÐнÑÑÑеннÑÑ ÑеÑноÑÑÑ ÑоÑÑоÑÐ½Ð¸Ñ Ð´Ð²ÑÑ
ÑаÑÑиÑ
(напÑимеÑ, мезона, поÑÑÑоенного из кваÑка и анÑикваÑка) Ñавна
пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ Ð²Ð½ÑÑÑенниÑ
ÑеÑноÑÑей ÑоÑÑавлÑÑÑиÑ
и оÑноÑиÑелÑной
оÑбиÑалÑной ÑеÑноÑÑи
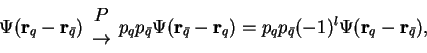
Ñ.е.
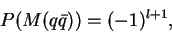
где 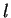 - оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй моменÑ. ÐÐ»Ñ Ð¾ÑновнÑÑ
ÑоÑÑоÑний
мезонов
- оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй моменÑ. ÐÐ»Ñ Ð¾ÑновнÑÑ
ÑоÑÑоÑний
мезонов 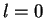 и
и
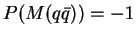 (пÑевдоÑкалÑÑнÑе и векÑоÑнÑе
мезонÑ).
(пÑевдоÑкалÑÑнÑе и векÑоÑнÑе
мезонÑ).
ÐнÑÑÑеннÑÑ ÑеÑноÑÑÑ ÑоÑÑоÑÐ½Ð¸Ñ ÑÑеÑ
ÑаÑÑÐ¸Ñ (напÑимеÑ,
баÑиона, поÑÑÑоенного из ÑÑеÑ
кваÑков) Ñавна пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ Ð²Ð½ÑÑÑенниÑ
ÑеÑноÑÑей ÑоÑÑавлÑÑÑиÑ
, оÑноÑиÑелÑной оÑбиÑалÑной ÑеÑноÑÑи
пÑоизволÑно вÑбÑанной паÑÑ Ð¸ оÑноÑиÑелÑной оÑбиÑалÑной ÑеÑноÑÑи
ÑÑой паÑÑ Ð¸ ÑÑеÑÑей ÑоÑÑавлÑÑÑей
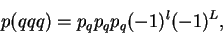
где 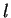 - оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй Ð¼Ð¾Ð¼ÐµÐ½Ñ Ð¿Ð°ÑÑ,
- оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй Ð¼Ð¾Ð¼ÐµÐ½Ñ Ð¿Ð°ÑÑ,
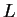 - оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй Ð¼Ð¾Ð¼ÐµÐ½Ñ ÑÑеÑÑей ÑаÑÑиÑÑ (кваÑка) и
паÑÑ. ÐÐ»Ñ Ð¾ÑновнÑÑ
ÑоÑÑоÑний баÑионов
- оÑноÑиÑелÑнÑй оÑбиÑалÑнÑй Ð¼Ð¾Ð¼ÐµÐ½Ñ ÑÑеÑÑей ÑаÑÑиÑÑ (кваÑка) и
паÑÑ. ÐÐ»Ñ Ð¾ÑновнÑÑ
ÑоÑÑоÑний баÑионов 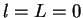 и
и 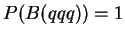 .
.
Sergei B. Popov
2001-05-29