[ ENGLISH ] [AUTO] [KOI-8R] [WINDOWS] [DOS]
[ISO-8859]
�


–Э–Є–Ї–Њ–ї–∞–є –Э–Є–Ї–Є—В–Є–љ
–Т–Њ–ї–љ–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞.
(–Ї 75-–ї–µ—В–Є—О —Б–Њ–Ј–і–∞–љ–Є—П)
–Я—А–µ–і—Л—Б—В–Њ—А–Є—П –Є –њ–µ—А–≤–Њ–µ —Б–Њ–Њ–±—Й–µ–љ–Є–µ
–Р–љ–љ–Њ—В–∞—Ж–Є—П
–Э–∞—Б—В–Њ—П—Й–∞—П —Б—В–∞—В—М—П –њ–Њ—Б–≤—П—Й–µ–љ–∞ 75-–ї–µ—В–Є—О —Б–Њ–Ј–і–∞–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –≤–Њ–ї–љ–Њ–≤–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–Є –≤ 1926 –≥–Њ–і—Г. –Я—А–µ–і–њ–Њ–ї–∞–≥–∞—О—В—Б—П —В—А–Є —З–∞—Б—В–Є. –Т –њ–µ—А–≤–Њ–є, –Ї–Њ—В–Њ—А—Г—О
–Т—Л —З–Є—В–∞–µ—В–µ —Б–µ–є—З–∞—Б, –Ї—А–∞—В–Ї–Њ –Њ—Б–≤–µ—Й–µ–љ–∞ –Є—Б—В–Њ—А–Є—П —Б–Њ–Ј–і–∞–љ–Є—П –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞, –Ї–Њ—В–Њ—А–∞—П –њ—А–µ–і—И–µ—Б—В–≤–Њ–≤–∞–ї–∞ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ
–®—А–µ–і–Є–љ–≥–µ—А–∞, –і–∞–љ –њ–Њ–і—А–Њ–±–љ—Л–є –њ–µ—А–µ—Б–Ї–∞–Ј —Б –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є—П–Љ–Є
–њ–µ—А–≤–Њ–є —Б—В–∞—В—М–Є –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –Є —Б–і–µ–ї–∞–љ–∞ –њ–Њ–њ—Л—В–Ї–∞
–Њ—В–≤–µ—В–Є—В—М –љ–∞ –≤–Њ–њ—А–Њ—Б, –њ–Њ—З–µ–Љ—Г –љ–µ—Б—В—А–Њ–≥–Є–є –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ –і–∞–ґ–µ –ї–Њ–≥–Є—З–µ—Б–Ї–Є
–њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–≤—Л–є –≤–Њ–ї–љ–Њ–≤–Њ–є –њ–Њ–і—Е–Њ–і –®—А–µ–і–Є–љ–≥–µ—А–∞ —Б—А–∞–Ј—Г –њ–Њ–ї—Г—З–Є–ї –њ—А–Є–Ј–љ–∞–љ–Є–µ
–≤–µ–і—Г—Й–Є—Е —Д–Є–Ј–Є–Ї–Њ–≤ —Б–≤–Њ–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є, –≤ —В–Њ –≤—А–µ–Љ—П –Ї–∞–Ї –ї–Њ–≥–Є—З–µ—Б–Ї–Є –Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є
–±–µ–Ј—Г–њ—А–µ—З–љ—Л–є –њ–Њ–і—Е–Њ–і "–≥–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Њ–є —И–Ї–Њ–ї—Л" –љ–µ –љ–∞—И–µ–ї –њ–Њ–і–Њ–±–∞—О—Й–µ–≥–Њ
–µ–Љ—Г –њ–Њ–љ–Є–Љ–∞–љ–Є—П –Є –Њ–і–Њ–±—А–µ–љ–Є—П.
–Ш—Б—В–Њ—А–Є—З–µ—Б–Ї–Є —Б–ї–Њ–ґ–Є–ї–Њ—Б—М —В–∞–Ї, —З—В–Њ —Б–Њ–Ј–і–∞–љ–Є–µ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є
—И–ї–Њ –і–≤—Г–Љ—П –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л–Љ–Є –Є –Њ—З–µ–љ—М –Њ—В–ї–Є—З–љ—Л–Љ–Є –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞ –њ—Г—В—П–Љ–Є.
–Ґ–Њ, —З—В–Њ –Њ–±–∞ —Н—В–Є –њ—Г—В–Є –≤ –Ї–Њ–љ—Ж–µ –Ї–Њ–љ—Ж–Њ–≤ –њ—А–Є–≤–µ–ї–Є –Ї —Б–Њ–Ј–і–∞–љ–Є—О –µ–і–Є–љ–Њ–є —В–µ–Њ—А–Є–Є
–Љ–Є–Ї—А–Њ–Љ–Є—А–∞, –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–љ–Њ–є –≤ –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –љ–µ –Њ–і–љ–Њ–є —Б–Њ—В–љ–µ–є —А–∞–Ј–ї–Є—З–љ—Л—Е
—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤, –і–Њ–ї–ґ–љ–Њ —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤–Њ–≤–∞—В—М –≤ –њ–Њ–ї—М–Ј—Г —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П
–Њ–±—К–µ–Ї—В–Є–≤–љ—Л—Е –Ј–∞–Ї–Њ–љ–Њ–≤, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є—Е –≤–љ—Г—В—А–µ–љ–љ—О—О –ї–Њ–≥–Є–Ї—Г —А–∞–Ј–≤–Є—В–Є—П
–µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л—Е –љ–∞—Г–Ї.
–Я–µ—А–≤—Л–є –њ—Г—В—М —Б–≤—П–Ј—Л–≤–∞–µ—В –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є —Д–Є–Ј–Є–Ї–Њ–≤ "–±–Њ—А–Њ–≤—Б–Ї–Њ–≥–Њ —В–Њ–ї–Ї–∞",
(–±–Њ–ї—М—И–Є–љ—Б—В–≤–Њ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –љ–∞ –Љ–Њ–Љ–µ–љ—В —Б–Њ–Ј–і–∞–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є —А–∞–±–Њ—В–∞–ї–Њ
–≤ –У–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Њ–Љ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–µ –≤ –У–µ—А–Љ–∞–љ–Є–Є), –Є –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Њ—Б–ї–µ–ґ–µ–љ –Њ—В
–њ–Є–Њ–љ–µ—А—Б–Ї–Њ–є —А–∞–±–Њ—В—Л 1913 –≥–Њ–і–∞ –≤—Л–і–∞—О—Й–µ–≥–Њ—Б—П –і–∞—В—Б–Ї–Њ–≥–Њ —Д–Є–Ј–Є–Ї–∞ –Э–Є–ї—М—Б–∞ –С–Њ—А–∞.
–Т —Б–≤–Њ–µ–є —А–∞–±–Њ—В–µ –С–Њ—А —Б—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞–ї –Ј–љ–∞–Љ–µ–љ–Є—В—Л–µ –Ї–≤–∞–љ—В–Њ–≤—Л–µ –њ–Њ—Б—В—Г–ї–∞—В—Л.
–≠—В–Є –њ–Њ—Б—В—Г–ї–∞—В—Л –Ј–∞–ї–Њ–ґ–Є–ї–Є –Њ—Б–љ–Њ–≤—Г —В–Њ–≥–Њ –њ–Њ–і—Е–Њ–і–∞ –Ї –Њ–њ–Є—Б–∞–љ–Є—О —П–≤–ї–µ–љ–Є–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞,
–њ—А–Є–і–µ—А–ґ–Є–≤–∞—П—Б—М –Ї–Њ—В–Њ—А–Њ–≥–Њ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є –Є —Г—З–µ–љ–Є–Ї–Є –Э.–С–Њ—А–∞, –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ,
—Б–∞–Љ—Л–є –≥–µ–љ–Є–∞–ї—М–љ—Л–є –Є–Ј –љ–Є—Е –Т–µ—А–љ–µ—А –У–µ–є–Ј–µ–љ–±–µ—А–≥, –њ—А–Є—И–ї–Є –Ї —Б–Њ–Ј–і–∞–љ–Є—О –≤–Њ –≤—В–Њ—А–Њ–є
–њ–Њ–ї–Њ–≤–Є–љ–µ 1925 –≥–Њ–і–∞ —Д–Њ—А–Љ–∞–ї–Є–Ј–Љ–∞ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є, –Ї–Њ—В–Њ—А—Л–є —Б–µ–≥–Њ–і–љ—П
–±–Њ–ї–µ–µ –њ—А–Є–≤—Л—З–љ–Њ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Є–Љ –Є–ї–Є –Љ–∞—В—А–Є—З–љ—Л–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ–Љ
–Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Ф–∞–љ–љ—Л–є –њ–Њ–і—Е–Њ–і —Б–≤—П–Ј–∞–љ —Б –Є–і–µ–µ–є —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж,
–њ–Њ —Б—Г—В–Є –і–µ–ї–∞, –Ї–∞–Ї –Їo—А–њ—Г—Б–Ї—Г–ї –Є –Њ–њ–Є—Б–∞–љ–Є—П –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—П –Љ–µ–ґ–і—Г
–љ–Є–Љ–Є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —В–Њ–ї—М–Ї–Њ —В–µ—Е –њ–Њ–љ—П—В–Є–є, –і–ї—П –Ї–Њ—В–Њ—А—Л—Е –Љ–Њ–ґ–љ–Њ —Г–Ї–∞–Ј–∞—В—М
–њ—А–Њ—Ж–µ–і—Г—А—Г –Є—Е —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Я—А–Є —Н—В–Њ–Љ –њ–µ—А–µ—Е–Њ–і –Љ–Є–Ї—А–Њ—Б–Є—Б—В–µ–Љ—Л
–Є–Ј –љ–∞—З–∞–ї—М–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П –≤ –Ї–Њ–љ–µ—З–љ–Њ–µ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –њ–Њ—Б—А–µ–і—Б—В–≤–Њ–Љ –љ–µ–Ї–Њ–µ–≥–Њ
–Ј–∞–≥–∞–і–Њ—З–љ–Њ–≥–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —Б–Ї–∞—З–Ї–∞, –∞ –≤–Њ–њ—А–Њ—Б—Л —В–Є–њ–∞ "–Ъ–∞–Ї–Њ–≤–Њ —Б–Њ—Б—В–Њ—П–љ–Є–µ —Н–ї–µ–Ї—В—А–Њ–љ–∞
–≤ —В–Њ –≤—А–µ–Љ—П, –Ї–Њ–≥–і–∞ –Њ–љ –њ–Њ—Б–ї–µ –∞–Ї—В–∞ –Є–Ј–ї—Г—З–µ–љ–Є—П –њ–µ—А–µ—Е–Њ–і–Є—В –≤ –∞—В–Њ–Љ–µ —Б –Њ–і–љ–Њ–є
–±–Њ—А–Њ–≤—Б–Ї–Њ–є –Њ—А–±–Є—В—Л –љ–∞ –і—А—Г–≥—Г—О?" –Њ–±—К—П–≤–ї—П–ї–Є—Б—М –љ–µ –Є–Љ–µ—О—Й–Є–Љ–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞,
–њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Б–Њ—Б—В–Њ—П–љ–Є–µ —Н–ї–µ–Ї—В—А–Њ–љ–∞, –±–µ–Ј –µ–≥–Њ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є—П, –≤ –Љ–Њ–Љ–µ–љ—В
–њ–µ—А–µ—Е–Њ–і–∞ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є–Ј–Љ–µ—А–µ–љ–Њ –љ–Є –Њ–і–љ–Є–Љ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ –њ—А–Є–±–Њ—А–Њ–Љ.
–Я–µ—А–≤–∞—П —А–∞–±–Њ—В–∞ –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ "–Ю –Ї–≤–∞–љ—В–Њ–≤–Њ—В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–Љ –Є—Б—В–Њ–ї–Ї–Њ–≤–∞–љ–Є–Є
–Ї–Є–љ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—Е –Є –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–є" [1] –њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О
–Њ–і–љ–Њ–≥–Њ –Є–Ј –≤–µ–і—Г—Й–Є—Е –≤ —В–Њ –≤—А–µ–Љ—П –љ–∞—Г—З–љ—Л—Е –ґ—Г—А–љ–∞–ї–Њ–≤ "Zeitschrift f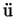 r
Physik" 29 –Є—О–ї—П 1925 –≥–Њ–і–∞. –≠—В–Њ—В –і–µ–љ—М –њ—А–Є–љ—П—В–Њ —Б—З–Є—В–∞—В—М –і–љ–µ–Љ —А–Њ–ґ–і–µ–љ–Є—П
—Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Т —Б–≤–Њ–µ–є —А–∞–±–Њ—В–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥, –≤–Њ-–њ–µ—А–≤—Л—Е,
–і–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ –†–Є—В—Ж–∞ –і–ї—П —Б–њ–µ–Ї—В—А–∞ —З–∞—Б—В–Њ—В –Є–Ј–ї—Г—З–µ–љ–Є—П
–∞—В–Њ–Љ–∞ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г –њ–Њ–љ—П—В–Є—О –Њ–± –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є —В—А–∞–µ–Ї—В–Њ—А–Є–Є
–і–≤–Є–ґ–µ–љ–Є—П —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤–љ—Г—В—А–Є –∞—В–Њ–Љ–∞, –≤–Њ-–≤—В–Њ—А—Л—Е, –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ —В–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ
–≤–µ–ї–Є—З–Є–љ—Л ("–њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є" –њ–Њ –У–µ–є–Ј–µ–љ–±–µ—А–≥—Г), –Ї–Њ—В–Њ—А—Л–µ –≤ –љ–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –і–Њ–ї–ґ–љ—Л
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞—В—М –љ–∞–±–ї—О–і–∞–µ–Љ—Л–Љ –љ–∞ –Њ–њ—Л—В–µ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ –≤–µ–ї–Є—З–Є–љ–∞–Љ, –≤ –Њ–±—Й–µ–Љ
—Б–ї—Г—З–∞–µ –љ–µ –Ї–Њ–Љ–Љ—Г—В–Є—А—Г—О—В –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ, –≤-—В—А–µ—В—М–Є—Е, –Њ–њ–Є—А–∞—П—Б—М –љ–∞ —В–µ–Њ—А–Є—О
–і–Є—Б–њ–µ—А—Б–Є–Є –Ъ—А–∞–Љ–µ—А—Б–∞, —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ—Г—О –Ј–∞ –≥–Њ–і –і–Њ —Н—В–Њ–≥–Њ, –њ–Њ–ї—Г—З–Є–ї –Ї–Њ–Љ—Г—В–∞—Ж–Є–Њ–љ–љ–Њ–µ
—Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–Љ—Г –і–Њ–ї–ґ–љ—Л —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—В—М –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є
–Є–Љ–њ—Г–ї—М—Б–∞ –Љ–Є–Ї—А–Њ—Б–Є—Б—В–µ–Љ—Л (–≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Њ–њ–µ—А–∞—В–Њ—А–љ–Њ–є –Ј–∞–њ–Є—Б–Є —Н—В–Њ —Е–Њ—А–Њ—И–Њ
–Є–Ј–≤–µ—Б—В–љ–Њ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ
r
Physik" 29 –Є—О–ї—П 1925 –≥–Њ–і–∞. –≠—В–Њ—В –і–µ–љ—М –њ—А–Є–љ—П—В–Њ —Б—З–Є—В–∞—В—М –і–љ–µ–Љ —А–Њ–ґ–і–µ–љ–Є—П
—Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Т —Б–≤–Њ–µ–є —А–∞–±–Њ—В–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥, –≤–Њ-–њ–µ—А–≤—Л—Е,
–і–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ –†–Є—В—Ж–∞ –і–ї—П —Б–њ–µ–Ї—В—А–∞ —З–∞—Б—В–Њ—В –Є–Ј–ї—Г—З–µ–љ–Є—П
–∞—В–Њ–Љ–∞ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г –њ–Њ–љ—П—В–Є—О –Њ–± –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є —В—А–∞–µ–Ї—В–Њ—А–Є–Є
–і–≤–Є–ґ–µ–љ–Є—П —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤–љ—Г—В—А–Є –∞—В–Њ–Љ–∞, –≤–Њ-–≤—В–Њ—А—Л—Е, –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ —В–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ
–≤–µ–ї–Є—З–Є–љ—Л ("–њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є" –њ–Њ –У–µ–є–Ј–µ–љ–±–µ—А–≥—Г), –Ї–Њ—В–Њ—А—Л–µ –≤ –љ–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –і–Њ–ї–ґ–љ—Л
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞—В—М –љ–∞–±–ї—О–і–∞–µ–Љ—Л–Љ –љ–∞ –Њ–њ—Л—В–µ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ –≤–µ–ї–Є—З–Є–љ–∞–Љ, –≤ –Њ–±—Й–µ–Љ
—Б–ї—Г—З–∞–µ –љ–µ –Ї–Њ–Љ–Љ—Г—В–Є—А—Г—О—В –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ, –≤-—В—А–µ—В—М–Є—Е, –Њ–њ–Є—А–∞—П—Б—М –љ–∞ —В–µ–Њ—А–Є—О
–і–Є—Б–њ–µ—А—Б–Є–Є –Ъ—А–∞–Љ–µ—А—Б–∞, —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ—Г—О –Ј–∞ –≥–Њ–і –і–Њ —Н—В–Њ–≥–Њ, –њ–Њ–ї—Г—З–Є–ї –Ї–Њ–Љ—Г—В–∞—Ж–Є–Њ–љ–љ–Њ–µ
—Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ, –Ї–Њ—В–Њ—А–Њ–Љ—Г –і–Њ–ї–ґ–љ—Л —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—В—М –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є
–Є–Љ–њ—Г–ї—М—Б–∞ –Љ–Є–Ї—А–Њ—Б–Є—Б—В–µ–Љ—Л (–≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Њ–њ–µ—А–∞—В–Њ—А–љ–Њ–є –Ј–∞–њ–Є—Б–Є —Н—В–Њ —Е–Њ—А–Њ—И–Њ
–Є–Ј–≤–µ—Б—В–љ–Њ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ
![${\rm [\hat x,\hat p]=i\hbar}$](img2.gif) ) –Є, –≤-—З–µ—В–≤–µ—А—В—Л—Е,
–њ–Њ–ї—М–Ј—Г—П—Б—М —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ, –У–µ–є–Ј–µ–љ–±–µ—А–≥ –љ–∞—И–µ–ї –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—А–Њ–≤–љ–Є —Н–љ–µ—А–≥–Є–Є
–ї–Є–љ–µ–є–љ–Њ–≥–Њ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ—Б—Ж–Є–ї—П—В–Њ—А–∞ –Є –Њ—Б—Ж–Є–ї—П—В–Њ—А–∞ —Б –∞–љ–≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є –і–Њ–±–∞–≤–Ї–Њ–є
–Ї —Н–љ–µ—А–≥–Є–Є –≤–Є–і–∞
) –Є, –≤-—З–µ—В–≤–µ—А—В—Л—Е,
–њ–Њ–ї—М–Ј—Г—П—Б—М —А–∞–Ј—А–∞–±–Њ—В–∞–љ–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ, –У–µ–є–Ј–µ–љ–±–µ—А–≥ –љ–∞—И–µ–ї –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—А–Њ–≤–љ–Є —Н–љ–µ—А–≥–Є–Є
–ї–Є–љ–µ–є–љ–Њ–≥–Њ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ—Б—Ж–Є–ї—П—В–Њ—А–∞ –Є –Њ—Б—Ж–Є–ї—П—В–Њ—А–∞ —Б –∞–љ–≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є –і–Њ–±–∞–≤–Ї–Њ–є
–Ї —Н–љ–µ—А–≥–Є–Є –≤–Є–і–∞
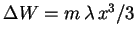 .
.
–Э–∞—Г—З–љ—Л–є —А—Г–Ї–Њ–≤–Њ–і–Є—В–µ–ї—М –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Є–Ј–≤–µ—Б—В–љ—Л–є –љ–µ–Љ–µ—Ж–Ї–Є–є —Д–Є–Ј–Є–Ї-—В–µ–Њ—А–µ—В–Є–Ї
–Ь–∞–Ї—Б –С–Њ—А–љ –Њ—З–µ–љ—М –±—Л—Б—В—А–Њ –њ–Њ–љ—П–ї, —З—В–Њ –≤–≤–µ–і–µ–љ–љ—Л—Е –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–µ–є
–Љ–Њ–ґ–љ–Њ –Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б —Н—А–Љ–Є—В–Њ–≤—Б–Ї–Є–Љ–Є –Љ–∞—В—А–Є—Ж–∞–Љ–Є, –∞ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—А–Њ–≤–љ–Є —Н–љ–µ—А–≥–Є–Є
—П–≤–ї—П—О—В—Б—П –љ–Є —З–µ–Љ –Є–љ—Л–Љ, –Ї–∞–Ї —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є —Н—А–Љ–Є—В–Њ–≤—Б–Ї–Њ–є
–Љ–∞—В—А–Є—Ж—Л –≥–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ–∞ —Б–Є—Б—В–µ–Љ—Л. –Т –У–µ—В—В–Є–љ–≥–µ–љ–µ –С–Њ—А–љ –љ–∞—И–µ–ї –Љ–Њ–ї–Њ–і–Њ–≥–Њ
—В–∞–ї–∞–љ—В–ї–Є–≤–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –Я–∞—Б–Ї—Г–∞–ї—П –Ш–Њ—А–і–∞–љ–∞, –Ї–Њ—В–Њ—А—Л–є —Е–Њ—А–Њ—И–Њ –Ј–љ–∞–ї
–Љ–∞—В—А–Є—З–љ–Њ–µ –Є—Б—З–Є—Б–ї–µ–љ–Є–µ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ—А–Є–Љ–µ—А–љ–Њ –Ј–∞ –≥–Њ–і –і–Њ –Њ–њ–Є—Б—Л–≤–∞–µ–Љ—Л—Е —Б–Њ–±—Л—В–Є–є
–њ–Њ–Љ–Њ–≥–∞–ї –і–≤—Г–Љ –≤–µ–ї–Є–Ї–Є–Љ –љ–µ–Љ–µ—Ж–Ї–Є–Љ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞–Љ –Ф–∞–≤–Є–і—Г –У–Є–ї—М–±–µ—А—В—Г –Є –†–Є—Е–∞—А–і—Г
–Ъ—Г—А–∞–љ—В—Г –≤ —Б–Њ—Б—В–∞–≤–ї–µ–љ–Є–Є –њ–µ—А–≤–Њ–≥–Њ —В–Њ–Љ–∞ –Ј–љ–∞–Љ–µ–љ–Є—В—Л—Е "–Ь–µ—В–Њ–і–Њ–≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є
—Д–Є–Ј–Є–Ї–Є" [2]. –Т —Н—В–Њ–є –Ї–љ–Є–≥–µ —Б –љ–µ–≤–µ—А–Њ—П—В–љ–Њ–є –њ—А–Њ–Ј–Њ—А–ї–Є–≤–Њ—Б—В—М—О
–Є–Ј–ї–∞–≥–∞–µ—В—Б—П –Ї–∞–Ї —А–∞–Ј —В–Њ—В –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –∞–њ–њ–∞—А–∞—В, –Ї–Њ—В–Њ—А—Л–є —Б—В–∞–љ–µ—В –љ–µ–Њ–±—Е–Њ–і–Є–Љ
—Д–Є–Ј–Є–Ї–∞–Љ –њ—А–Є —Б–Њ–Ј–і–∞–љ–Є–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є.
–Т —Б–Њ–∞–≤—В–Њ—А—Б—В–≤–µ —Б –Ш–Њ—А–і–∞–љ–Њ–Љ, –∞ –Ј–∞ —В–µ–Љ –Є —Б –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ, –С–Њ—А–љ –±—Л—Б—В—А–Њ
–љ–∞–њ–Є—Б–∞–ї –і–≤–µ —Б—В–∞—В—М–Є [3], –≤ –Ї–Њ—В–Њ—А—Л—Е, –њ–Њ —Б—Г—Й–µ—Б—В–≤—Г, –Є–Ј–ї–Њ–ґ–µ–љ –њ–Њ–ї–љ—Л–є
–Ї—Г—А—Б –ї–Є–љ–µ–є–љ–Њ–є –∞–ї–≥–µ–±—А—Л, –∞–і–∞–њ—В–Є—А–Њ–≤–∞–љ–љ—Л–є –Ї —А–µ—И–µ–љ–Є—О –Ј–∞–і–∞—З –љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є,
–Ї–Њ—В–Њ—А–∞—П —Б —В–µ—Е –њ–Њ—А –њ–Њ–ї—Г—З–Є–ї–∞ –љ–∞–Ј–≤–∞–љ–Є–µ –Љ–∞—В—А–Є—З–љ–Њ–є. –Ф–ї—П –њ–Њ–љ–Є–Љ–∞–љ–Є—П —Б—Г—В–Є –њ—А–Њ–±–ї–µ–Љ—Л,
–љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–±—А–∞—В–Є—В—М –≤–љ–Є–Љ–∞–љ–Є–µ –љ–∞ —В–Њ, —З—В–Њ –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є XX –≤–µ–Ї–∞ —В–µ–Њ—А–Є—П
–Љ–∞—В—А–Є—Ж –Њ—В–љ—О–і—М –љ–µ –≤—Е–Њ–і–Є–ї–∞ –≤ —Б—В–∞–љ–і–∞—А—В–љ—Л–µ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В—Б–Ї–Є–µ –Ї—Г—А—Б—Л –і–∞–ґ–µ –і–ї—П
–Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–≤ –Є, —В–µ–Љ –±–Њ–ї–µ–µ, –љ–µ –±—Л–ї–∞ –Є–Ј–≤–µ—Б—В–љ–∞ –њ–Њ–і–∞–≤–ї—П—О—Й–µ–Љ—Г –±–Њ–ї—М—И–Є–љ—Б—В–≤—Г
—Д–Є–Ј–Є–Ї–Њ–≤-—В–µ–Њ—А–µ—В–Є–Ї–Њ–≤, –∞ –њ–Њ—В–Њ–Љ—Г –љ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–∞—Б—М –Є–Љ–Є –≤ —Б–≤–Њ–Є—Е —А–∞–±–Њ—В–∞—Е.
–Э–∞–њ—А–Є–Љ–µ—А, –≤ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –≤–Љ–µ—Б—В–Њ –Љ–∞—В—А–Є—З–љ–Њ–≥–Њ –Є—Б—З–Є—Б–ї–µ–љ–Є—П –≤–њ–ї–Њ—В—М
–і–Њ –≤—В–Њ—А–Њ–є –њ–Њ–ї–Њ–≤–Є–љ—Л XX –≤–µ–Ї–∞ –≥–Њ—Б–њ–Њ–і—Б—В–≤–Њ–≤–∞–ї –≥—А–Њ–Љ–Њ–Ј–і–Ї–Є–є –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–є
–Љ–µ—В–Њ–і. –Т –љ–∞—З–∞–ї–µ XX –≤–µ–Ї–∞ –њ–Њ—П–≤–Є–ї–∞—Б—М —В–Њ–ї—М–Ї–Њ –Њ–і–љ–∞ –і–Њ—Б—В–Њ–є–љ–∞—П —Г–њ–Њ–Љ–Є–љ–∞–љ–Є—П
—Д–Є–Ј–Є—З–µ—Б–Ї–∞—П —В–µ–Њ—А–Є—П, –≤ –Ї–Њ—В–Њ—А–Њ–є –Љ–∞—В—А–Є—Ж—Л –Є–≥—А–∞–ї–Є –≤–∞–ґ–љ—Г—О —А–Њ–ї—М. –≠—В–Њ –љ–µ–ї–Є–љ–µ–є–љ–∞—П
—Н–ї–µ–Ї—В—А–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –Є —В–µ–Њ—А–Є—П —В—П–≥–Њ—В–µ–љ–Є—П –У—Г—Б—В–∞–≤–∞ –Ь–Є. –Э–Њ –Њ–љ–∞ –±—Л–ї–∞ –Њ—В–≤–µ—А–≥–љ—Г—В–∞
–Є –Њ—Б–љ–Њ–≤–∞—В–µ–ї—М–љ–Њ –Ј–∞–±—Л—В–∞ –њ–Њ—Б–ї–µ –њ–Њ—П–≤–ї–µ–љ–Є—П –Є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–Є—П
–Њ–±—Й–µ–є —В–µ–Њ—А–Є–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є –Р.–≠–є–љ—И—В–µ–є–љ–∞. –Ы—О–±–Њ–њ—Л—В–љ–Њ, —З—В–Њ –і–∞–ґ–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥,
–њ–Њ–ї—Г—З–Є–≤—И–Є–є —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–Њ–µ —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В—Б–Ї–Њ–µ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –≤ –Ь—О–љ—Е–µ–љ–µ —Г —Б–∞–Љ–Њ–≥–Њ
–Р—А–љ–Њ–ї—М–і–∞ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ (–Я–Њ–Љ–љ–Є—В–µ, "–љ–µ—В –С–Њ–≥–∞ –Ї—А–Њ–Љ–µ –С–Њ—А–∞ –Є –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і –њ—А–Њ—А–Њ–Ї
–µ–≥–Њ"?), –љ–µ –Ј–љ–∞–ї, —З—В–Њ —В–∞–Ї–Њ–µ –Љ–∞—В—А–Є—Ж–∞, –Є —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ –≤—Л–і—Г–Љ–∞–ї –Љ–∞—В—А–Є—З–љ–Њ–µ
–Є—Б—З–Є—Б–ї–µ–љ–Є–µ, –Є—Б—Е–Њ–і—П –Є–Ј —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е —В—А–µ–±–Њ–≤–∞–љ–Є–є, –Ї–Њ—В–Њ—А—Л–µ –њ—А–µ–і—К—П–≤–ї—П—О—В—Б—П
–Ї –њ—А–Њ—Ж–µ—Б—Б—Г –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–Њ—Б—В–Њ—П–љ–Є—П –Љ–Є–Ї—А–Њ—Б–Є—Б—В–µ–Љ—Л. –У–Њ–≤–Њ—А—П—В, —З—В–Њ –Ї–Њ–≥–і–∞ –Њ–± —Н—В–Њ–Љ
—Г–Ј–љ–∞–ї –і—А—Г–≥–Њ–є "–Љ–Њ–ї–Њ–і–Њ–є —В–Є–≥—А" –Њ—В —Д–Є–Ј–Є–Ї–Є –Т–Њ–ї—М—Д–≥–∞–љ–≥ –Я–∞—Г–ї–Є, —В–Њ –≤–Њ—Б–Ї–ї–Є–Ї–љ—Г–ї:
"–У–Њ—Б–њ–Њ–і–Є, –Ї–∞–Ї–Њ–є –У–Х–Э–Ш–Р–Ы–ђ–Э–Ђ–Щ –љ–µ–≤–µ–ґ–∞, —Н—В–Њ—В –У–µ–є–Ј–µ–љ–±–µ—А–≥!" –Я–Њ—Б–ї–µ–і–љ—П—П —В–Њ—З–Ї–∞
–≤ –њ—А–Њ–≤–µ—А–Ї–µ –њ—А–∞–≤–Є–ї—М–љ–Њ—Б—В–Є –Њ—Б–љ–Њ–≤–љ—Л—Е –њ—А–Є–љ—Ж–Є–њ–Њ–≤ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –±—Л–ї–∞
–њ–Њ—Б—В–∞–≤–ї–µ–љ–∞ 17 —П–љ–≤–∞—А—П 1926 –≥–Њ–і–∞, –Ї–Њ–≥–і–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О –ґ—Г—А–љ–∞–ї–∞ "Zeitschrift
f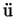 r Physik" –њ–Њ—Б—В—Г–њ–Є–ї–∞ —Б—В–∞—В—М—П –≤—Б–µ —В–Њ–≥–Њ –ґ–µ –Я–∞—Г–ї–Є "–Ю —Б–њ–µ–Ї—В—А–µ
–≤–Њ–і–Њ—А–Њ–і–∞ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –љ–Њ–≤–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є" [4]. –Т —Н—В–Њ–є
—А–∞–±–Њ—В–µ —Б–Ї–Њ–ї—М —Г—Б–њ–µ—И–љ–Њ —Б—В–Њ–ї—М –Є –Є–Ј—П—Й–љ–Њ —А–µ—И–µ–љ–∞ –Ј–∞–і–∞—З–∞ –Њ –і–Є–∞–≥–Њ–љ–∞–ї–Є–Ј–∞—Ж–Є–Є
–≥–∞–Љ–Є–ї—М—В–Њ–љ–Њ–≤–Њ–є –Љ–∞—В—А–Є—Ж—Л –≤–Њ–і–Њ—А–Њ–і–Њ–њ–Њ–і–Њ–±–љ–Њ–≥–Њ –∞—В–Њ–Љ–∞ –Є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ –∞—В–Њ–Љ–∞
–≤–Њ –≤–љ–µ—И–љ–Є—Е –њ–Њ–ї—П—Е. –° –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –Ј–∞–і–∞—З–∞ –Њ–Ї–∞–Ј–∞–ї–∞—Б—М –љ–µ–≤–µ—А–Њ—П—В–љ–Њ
—В—А—Г–і–љ–Њ–є. –°—В–Њ–Є—В –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –і—А—Г–≥–Њ–є –Ј–љ–∞–Љ–µ–љ–Є—В—Л–є —В–µ–Њ—А–µ—В–Є–Ї –Я–Њ–ї—М –Р–і—А–Є–µ–љ –Ь–Њ—А–Є—Б
–Ф–Є—А–∞–Ї –њ–Њ—В–µ—А–њ–µ–ї –љ–µ—Г–і–∞—З—Г, –њ—Л—В–∞—П—Б—М –µ–µ —А–µ—И–Є—В—М. –Э–∞ —Н—В–Њ–Љ, –њ–Њ —Б—Г—Й–µ—Б—В–≤—Г, –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ
–Ї–≤–∞–љ—В–Њ–≤–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ —Б—З–Є—В–∞—В—М –Ј–∞–≤–µ—А—И–µ–љ–љ—Л–Љ.
r Physik" –њ–Њ—Б—В—Г–њ–Є–ї–∞ —Б—В–∞—В—М—П –≤—Б–µ —В–Њ–≥–Њ –ґ–µ –Я–∞—Г–ї–Є "–Ю —Б–њ–µ–Ї—В—А–µ
–≤–Њ–і–Њ—А–Њ–і–∞ —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –љ–Њ–≤–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є" [4]. –Т —Н—В–Њ–є
—А–∞–±–Њ—В–µ —Б–Ї–Њ–ї—М —Г—Б–њ–µ—И–љ–Њ —Б—В–Њ–ї—М –Є –Є–Ј—П—Й–љ–Њ —А–µ—И–µ–љ–∞ –Ј–∞–і–∞—З–∞ –Њ –і–Є–∞–≥–Њ–љ–∞–ї–Є–Ј–∞—Ж–Є–Є
–≥–∞–Љ–Є–ї—М—В–Њ–љ–Њ–≤–Њ–є –Љ–∞—В—А–Є—Ж—Л –≤–Њ–і–Њ—А–Њ–і–Њ–њ–Њ–і–Њ–±–љ–Њ–≥–Њ –∞—В–Њ–Љ–∞ –Є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ –∞—В–Њ–Љ–∞
–≤–Њ –≤–љ–µ—И–љ–Є—Е –њ–Њ–ї—П—Е. –° –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –Ј–∞–і–∞—З–∞ –Њ–Ї–∞–Ј–∞–ї–∞—Б—М –љ–µ–≤–µ—А–Њ—П—В–љ–Њ
—В—А—Г–і–љ–Њ–є. –°—В–Њ–Є—В –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –і—А—Г–≥–Њ–є –Ј–љ–∞–Љ–µ–љ–Є—В—Л–є —В–µ–Њ—А–µ—В–Є–Ї –Я–Њ–ї—М –Р–і—А–Є–µ–љ –Ь–Њ—А–Є—Б
–Ф–Є—А–∞–Ї –њ–Њ—В–µ—А–њ–µ–ї –љ–µ—Г–і–∞—З—Г, –њ—Л—В–∞—П—Б—М –µ–µ —А–µ—И–Є—В—М. –Э–∞ —Н—В–Њ–Љ, –њ–Њ —Б—Г—Й–µ—Б—В–≤—Г, –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ
–Ї–≤–∞–љ—В–Њ–≤–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ —Б—З–Є—В–∞—В—М –Ј–∞–≤–µ—А—И–µ–љ–љ—Л–Љ.
–Ю–і–љ–∞–Ї–Њ, –≤–Њ–њ—А–µ–Ї–Є –≤–њ–µ—З–∞—В–ї—П—О—Й–Є–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Ї–∞–Ї –њ—А–Є –Њ–±—К—П—Б–љ–µ–љ–Є–Є —П–≤–ї–µ–љ–Є–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞,
—В–∞–Ї –Є –њ—А–Є —А–∞–Ј—А–∞–±–Њ—В–Ї–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞, –Љ–∞—В—А–Є—З–љ–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –≤—Б—В—А–µ—З–∞–ї–∞—Б—М
–≤ —И—В—Л–Ї–Є –Љ–љ–Њ–≥–Є–Љ–Є —Д–Є–Ј–Є–Ї–∞–Љ–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є. –Э–∞ —В–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ—А–Є—З–Є–љ.
–Я–µ—А–≤–Њ–є –≤ –Є—Е —А—П–і—Г —Б—В–Њ–Є—В –љ–∞–Ј–≤–∞—В—М —В—А—Г–і–љ–Њ—Б—В—М —Б –њ–Њ–љ–Є–Љ–∞–љ–Є–µ–Љ –љ–µ–њ—А–Є–≤—Л—З–љ–Њ–≥–Њ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞ —В–µ–Њ—А–Є–Є –Є –Є—Б–Ї–ї—О—З–Є—В–µ–ї—М–љ—Г—О —В—А—Г–і–Њ–µ–Љ–Ї–Њ—Б—В—М —Г–љ–Є–≤–µ—А—Б–∞–ї—М–љ–Њ–≥–Њ
–∞–ї–≥–Њ—А–Є—В–Љ–∞ –і–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–є —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–њ–µ–Ї—В—А–∞
–Ї–≤–∞–љ—В–Њ–≤–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ. –Ш–Ј-–Ј–∞ —Н—В–Њ–≥–Њ
–Љ–∞—В—А–Є—З–љ—Г—О –Љ–µ—Е–∞–љ–Є–Ї—Г –љ–∞–Ј—Л–≤–∞–ї–Є "—В–Є–њ–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј—Ж–Њ–Љ –≥–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Њ–є —Г—З–µ–љ–Њ—Б—В–Є", —З—В–Њ
—Б –Њ–±—В–µ–Ї–∞–µ–Љ–Њ–≥–Њ –љ–µ–Љ–µ—Ж–Ї–Њ–≥–Њ –љ–∞ –њ–Њ–љ—П—В–љ—Л–є —А—Г—Б—Б–Ї–Є–є –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–≤–µ—Б—В–Є –Ї–∞–Ї "—Б—В—А–∞—И–љ–∞—П
–Ј–∞—Г–Љ—М, –≤—Л–і—Г–Љ–∞–љ–∞—П –љ–∞ –љ–∞—И—Г –≥–Њ–ї–Њ–≤—Г –≥–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Є–Љ–Є –Ј–∞–љ—Г–і–∞–Љ–Є". –Т—В–Њ—А–Њ–є –њ—А–Є—З–Є–љ–Њ–є,
–љ–µ—Б–Њ–Љ–љ–µ–љ–љ–Њ, —П–≤–ї—П–ї–Њ—Б—М —В–Њ, —З—В–Њ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї —В–µ–Њ—А–Є–Є –±—Л–ї –∞–±—Б–Њ–ї—О—В–љ–Њ –љ–µ
–њ—А–Њ—П—Б–љ–µ–љ. –Ы—О–і–µ–є —Б–Њ –Ј–љ–∞–љ–Є–µ–Љ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є –Њ—Б–Њ–±–µ–љ–љ–Њ –љ–µ—А–≤–Є—А–Њ–≤–∞–ї–Є –≤—Б–µ
—Н—В–Є –љ–µ–њ–Њ–љ—П—В–љ—Л–µ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Б–Ї–∞—З–Ї–Є –Є "–Ј–∞–≥–∞–і–Њ—З–љ–∞—П" –і–Є—Б–Ї—А–µ—В–љ–Њ—Б—В—М, –Ї–Њ—В–Њ—А—Л–µ –љ–µ
–Є–Љ–µ—О—В –∞–љ–∞–ї–Њ–≥–Њ–≤ –≤ –Ї–ї–∞—Б—Б–Є–Ї–µ, –љ–Њ —Б–Њ –≤—А–µ–Љ–µ–љ –Я–ї–∞–љ–Ї–∞ –њ—А–Њ—З–љ–Њ —Г–≥–љ–µ–Ј–і–Є–ї–Є—Б—М –≤
—Д–Є–Ј–Є–Ї–µ. –Р —В–µ–њ–µ—А—М –Ї –љ–Є–Љ –і–Њ–±–∞–≤–Є–ї–∞—Б—М –љ–Њ–≤–∞—П –±–µ–і–∞: –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –њ—А–Є–њ–Є—Б–∞—В—М
–Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Г—О —В—А–∞–µ–Ї—В–Њ—А–Є—О –і–≤–Є–ґ–µ–љ–Є—П. –Я–Њ–љ–∞–і–Њ–±–Є–ї–Њ—Б—М –µ—Й–µ –Њ–Ї–Њ–ї–Њ
–і–µ—Б—П—В–Є –ї–µ—В, —З—В–Њ–±—Л –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ—А–Њ—П—Б–љ–Є—В—М —Б—В–∞—В—Г—Б –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–Ї–∞—З–Ї–Њ–≤ –Є
—В—А–∞–µ–Ї—В–Њ—А–Є–є –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж –≤ —Б–Њ–Ј–і–∞–љ–љ–Њ–є –С–Њ—А–Њ–Љ –Є –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ –Ї–Њ–њ–µ–љ–≥–∞–≥–µ–љ—Б–Ї–Њ–є
–Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –•–Њ—В—П –њ–Њ–ї–љ–Њ–є —П—Б–љ–Њ—Б—В–Є –≤ —Н—В–Њ–Љ –≤–Њ–њ—А–Њ—Б–µ –љ–µ—В –і–Њ
—Б–Є—Е –њ–Њ—А. –Ъ–≤–∞–љ—В–Њ–≤–∞—П —В–µ–Њ—А–Є—П - –µ–і–Є–љ—Б—В–≤–µ–љ–љ–∞—П —Д–Є–Ј–Є—З–µ—Б–Ї–∞—П —В–µ–Њ—А–Є—П, –Ї–Њ—В–Њ—А–∞—П –Є–Љ–µ–µ—В
–љ–µ –Њ–і–љ—Г, –∞ –љ–µ –Љ–µ–љ–µ–µ —З–µ—В—Л—А–µ—Е —А–∞–Ј–ї–Є—З–љ—Л—Е —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–є –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ–Њ–≥–Њ
–≤ –љ–µ–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞ (–Ї–Њ–њ–µ–љ–≥–∞–≥–µ–љ—Б–Ї—Г—О, —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї—Г—О, –Љ–љ–Њ–≥–Њ–Љ–Є—А–Њ–≤—Г—О
–Є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Њ–љ–љ—Г—О –Є–ї–Є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О). –Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ—В–Љ–µ—В–Є—В—М, —З—В–Њ
—Е–Њ—В—П –≤ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –Љ–љ–Њ–≥–Њ –≤–љ–Є–Љ–∞–љ–Є—П —Г–і–µ–ї—П–ї–Њ—Б—М —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ
–Ј–љ–∞—З–µ–љ–Є—П–Љ —Н—А–Љ–Є—В–Њ–≤—Б–Ї–Є—Е –Љ–∞—В—А–Є—Ж –Є –Є—Е —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–Љ—Г —Б–Љ—Л—Б–ї—Г, –љ–Є–Ї—В–Њ –≤ —В–Њ –≤—А–µ–Љ—П
–љ–µ –Ј–∞–і—Г–Љ—Л–≤–∞–ї—Б—П –Њ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–Љ —Б–Љ—Л—Б–ї–µ –љ–∞–±–Њ—А–∞ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤, –Њ—В–≤–µ—З–∞—О—Й–Є—Е
–і–∞–љ–љ—Л–Љ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ –Ј–љ–∞—З–µ–љ–Є—П–Љ, –≤ –±–∞–Ј–Є—Б–µ –Ї–Њ—В–Њ—А—Л—Е —Н—А–Љ–Є—В–Њ–≤—Б–Ї–∞—П –Љ–∞—В—А–Є—Ж–∞
–Є–Љ–µ–ї–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М–љ—Л–є –≤–Є–і! –Э–µ –њ–Њ—Б–ї–µ–і–љ—О—О —А–Њ–ї—М –≤ —Е–Њ–ї–Њ–і–љ–Њ–Љ –њ—А–Є–µ–Љ–µ –љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є,
–≤–Є–і–Є–Љ–Њ, —Б—Л–≥—А–∞–ї–Њ –Є –љ–µ–њ—А–Є—П–Ј–љ–µ–љ–љ–Њ–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –Њ–і–љ–Њ–≥–Њ –Є–Ј –≤–µ–ї–Є—З–∞–є—И–Є—Е –љ–µ–Љ–µ—Ж–Ї–Є—Е
—Д–Є–Ј–Є–Ї–Њ–≤-—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞—В–Њ—А–Њ–≤ –Т–Є–ї—М–≥–µ–ї—М–Љ–∞ –Т–Є–љ–∞ –ї–Є—З–љ–Њ –Ї –Т–µ—А–љ–µ—А—Г –У–µ–є–Ј–µ–љ–±–µ—А–≥—Г. –Ф–µ–ї–Њ
–≤ —В–Њ–Љ, —З—В–Њ –Ј–∞ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –ї–µ—В –і–Њ –Њ–њ–Є—Б—Л–≤–∞–µ–Љ—Л—Е —Б–Њ–±—Л—В–Є–є –У–µ–є–Ј–µ–љ–±–µ—А–≥ –њ–Њ–Ј–Њ—А–љ–Њ
–њ—А–Њ–≤–∞–ї–Є–ї—Б—П –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–µ —Г –Т–Є–љ–∞, –њ–Њ–Ї–∞–Ј–∞–≤ —Б–≤–Њ–µ –њ–Њ–ї–љ–Њ–µ –љ–µ–Ј–љ–∞–љ–Є–µ –Њ—Б–љ–Њ–≤–љ—Л—Е
—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –Љ–µ—В–Њ–і–Њ–≤ —Д–Є–Ј–Є–Ї–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є. –Ґ–Њ–ї—М–Ї–Њ –ї–Є—З–љ–∞—П –њ—А–Њ—Б—М–±–∞
–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ —Б–њ–∞—Б–ї–∞ –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Њ—В —А–µ–∞–ї—М–љ–Њ–є –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –Њ—Б—В–∞—В—М—Б—П –±–µ–Ј
—Г–љ–Є–≤–µ—А—Б–Є—В–µ—В—Б–Ї–Њ–≥–Њ –і–Є–њ–ї–Њ–Љ–∞. –° —В–µ—Е –њ–Њ—А –Є –і–Њ –Ї–Њ–љ—Ж–∞ —Б–≤–Њ–µ–є –ґ–Є–Ј–љ–Є –Т–Є–љ —Б—З–Є—В–∞–ї
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Љ–Њ–ї–Њ–і—Л–Љ –≤—Л—Б–Ї–Њ—З–Ї–Њ–є-–љ–µ—Г—З–µ–Љ.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Љ–љ–Њ–≥–Є–µ —Д–Є–Ј–Є–Ї–Є –њ–Њ —А–∞–Ј–љ—Л–Љ –њ—А–Є—З–Є–љ–∞–Љ –љ–µ –њ—А–Є–љ—П–ї–Є –Љ–∞—В—А–Є—З–љ—Г—О
—В–µ–Њ—А–Є—О –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞ –Є —Б—В—А–∞—Б—В–љ–Њ –ґ–µ–ї–∞–ї–Є, —З—В–Њ–±—Л —Б–Њ –≤—А–µ–Љ–µ–љ–µ–Љ
(–ї—Г—З—И–µ, –Ї–∞–Ї –Љ–Њ–ґ–љ–Њ —Б–Ї–Њ—А–µ–µ!) –Њ–љ–∞ –±—Л–ї–∞ –Ј–∞–Љ–µ–љ–µ–љ–∞ –і—А—Г–≥–Њ–є —В–µ–Њ—А–Є–µ–є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞,
–≤ –Ї–Њ—В–Њ—А–Њ–є –љ–µ –Њ—Б—В–∞–ї–Њ—Б—М –±—Л –Љ–µ—Б—В–∞ —Н—В–Є–Љ —Г–ґ–∞—Б–љ—Л–Љ –Ї–≤–∞–љ—В–Њ–≤—Л–Љ —Б–Ї–∞—З–Ї–∞–Љ, –Љ–∞—В—А–Є—Ж–∞–Љ
–Є —В–Њ–Љ—Г –њ–Њ–і–Њ–±–љ–Њ–є –ґ—Г—В–Є, —З—В–Њ–±—Л —Н—В–∞ –і—А—Г–≥–∞—П —В–µ–Њ—А–Є—П —Е–Њ—В—П –±—Л –Њ—В–і–∞–ї–µ–љ–љ–Њ –љ–∞–њ–Њ–Љ–Є–љ–∞–ї–∞
–њ—А–µ–ґ–љ–Є–µ —Г—О—В–љ—Л–µ —В–µ–Њ—А–Є–Є —Б –Є—Е –љ–µ–њ—А–µ—А—Л–≤–љ–Њ—Б—В—М—О, –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–Љ–Є —В—А–∞–µ–Ї—В–Њ—А–Є—П–Љ–Є
–Є –њ—А–Є–≤—Л—З–љ—Л–Љ–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ–Є —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є, –Њ–њ–Є—Б—Л–≤–∞—О—Й–Є–Љ–Є —Н—В–Є —В—А–∞–µ–Ї—В–Њ—А–Є–Є.
–Ш–Љ–µ–љ–љ–Њ –≤ —Б–Є—В—Г–∞—Ж–Є–Є –њ–Њ–і—Б–њ—Г–і–љ–Њ–≥–Њ –Њ–ґ–Є–і–∞–љ–Є—П –±–Њ–ї—М—И–Є–љ—Б—В–≤–Њ–Љ —Д–Є–Ј–Є–Ї–Њ–≤
–њ–Њ—П–≤–ї–µ–љ–Є—П "–љ–Њ–≤–Њ–є-—Б—В–∞—А–Њ–є" —В–µ–Њ—А–Є–Є –Љ–Є–Ї—А–Њ–Љ–Є—А–∞ 27 —П–љ–≤–∞—А—П 1926 –≥–Њ–і–∞
–≤ —А–µ–і–∞–Ї—Ж–Є—О –љ–µ–Љ–µ—Ж–Ї–Њ–≥–Њ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ –ґ—Г—А–љ–∞–ї–∞ "Annalen der Physik" –њ–Њ—Б—В—Г–њ–Є–ї–∞
–њ–µ—А–≤–∞—П –Є–Ј —Ж–µ–ї–Њ–є —Б–µ—А–Є–Є —А–∞–±–Њ—В –∞–≤—Б—В—А–Є–є—Б–Ї–Њ–≥–Њ —Д–Є–Ј–Є–Ї–∞ –≠—А–≤–Є–љ–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞, –≤
–Ї–Њ—В–Њ—А–Њ–є, –Ї–∞–Ї –Њ—И–Є–±–Њ—З–љ–Њ –Љ–Њ–≥–ї–Њ –њ–Њ–Ї–∞–Ј–∞—В—М—Б—П —Б–љ–∞—З–∞–ї–∞, —Б–Њ–і–µ—А–ґ–Є—В—Б—П —Б—В–Њ–ї—М
–ґ–µ–ї–∞–љ–љ–Њ–µ —А–µ—И–µ–љ–Є–µ –≤—Б–µ—Е –њ—А–Њ–±–ї–µ–Љ. –°—В–∞—В—М—П –љ–∞–Ј—Л–≤–∞–ї–∞—Б—М "–Ъ–≤–∞–љ—В–Њ–≤–∞–љ–Є–µ
–Ї–∞–Ї –Ј–∞–і–∞—З–∞ –Њ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е" ("Quantisierung als Eigenwertproblem").
–Т —Н—В–Њ–є —А–∞–±–Њ—В–µ –Є –њ—П—В–Є –њ–Њ—Б–ї–µ–і—Г—О—Й–Є—Е –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –±—Л–ї–Є –Ј–∞–ї–Њ–ґ–µ–љ—Л –Њ—Б–љ–Њ–≤—Л
–≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –°–њ—Г—Б—В—П 35 –ї–µ—В –Ь–∞–Ї—Б –С–Њ—А–љ –њ–Є—Б–∞–ї: "–І—В–Њ —Б—Г—Й–µ—Б—В–≤—Г–µ—В
–±–Њ–ї–µ–µ –≤—Л–і–∞—О—Й–µ–≥–Њ—Б—П –≤ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–µ, —З–µ–Љ –µ–≥–Њ (–®—А–µ–і–Є–љ–≥–µ—А–∞ - –Э.–Э.)
–њ–µ—А–≤—Л–µ —И–µ—Б—В—М —А–∞–±–Њ—В –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ?" ([5] —Б—В—А.384).
–Т "–њ–µ—А–≤—Л–µ —И–µ—Б—В—М —А–∞–±–Њ—В" –®—А–µ–і–Є–љ–≥–µ—А–∞, –±—Г–Ї–≤–∞–ї—М–љ–Њ –≤–Њ—Б–њ–µ—В—Л–µ –С–Њ—А–љ–Њ–Љ, –≤—Е–Њ–і—П—В —З–µ—В—Л—А–µ
—Б—В–∞—В—М–Є –њ–Њ–і –Њ–±—Й–Є–Љ –љ–∞–Ј–≤–∞–љ–Є–µ–Љ "–Ъ–≤–∞–љ—В–Њ–≤–∞–љ–Є–µ –Ї–∞–Ї –Ј–∞–і–∞—З–∞ –Њ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е",
–њ–µ—А–≤—Г—О –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –Љ—Л –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–±–µ—А–µ–Љ –љ–Є–ґ–µ, —А–∞–±–Њ—В–∞ "–Ю–± –Њ—В–љ–Њ—И–µ–љ–Є–Є
–Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞ –Ї –Љ–Њ–µ–є", –≤ –Ї–Њ—В–Њ—А–Њ–є –њ–Њ–Ї–∞–Ј–∞–љ–∞
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ—Б—В—М –Љ–∞—В—А–Є—З–љ–Њ–є –Є –≤–Њ–ї–љ–Њ–≤–Њ–Є –Љ–µ—Е–∞–љ–Є–Ї, –Є —А–∞–±–Њ—В–∞
"–Э–µ–њ—А–µ—А—Л–≤–љ—Л–є –њ–µ—А–µ—Е–Њ–і –Њ—В –Љ–Є–Ї—А–Њ- –Ї –Љ–∞–Ї—А–Њ–Љ–µ—Е–∞–љ–Є–Ї–µ" - —Б–∞–Љ–∞—П —Б–ї–∞–±–∞—П –≤ —Ж–Є–Ї–ї–µ,
–љ–Њ —Б–Є–ї—М–љ–Њ –њ–Њ–≤–ї–Є—П–≤—И–∞—П –љ–∞ –≤–Ј–≥–ї—П–і—Л —Б–∞–Љ–Њ–≥–Њ –®—А–µ–і–Є–љ–≥–µ—А–∞, –Ї–Њ—В–Њ—А—Л–є –њ–Њ—З—В–Є –і–Њ –Ї–Њ–љ—Ж–∞
—Б–≤–Њ–µ–є –ґ–Є–Ј–љ–Є –њ—Л—В–∞–ї—Б—П —Б—В—А–Њ–Є—В—М –Ї–Њ–Љ–њ–∞–Ї—В–љ—Л–µ –≤–Њ–ї–љ–Њ–≤—Л–µ –њ–∞–Ї–µ—В—Л, –Ї–Њ—В–Њ—А—Л–µ –±—Л
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Њ–≤–∞–ї–Є –і–≤–Є–ґ–µ–љ–Є—О –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж, —В–∞–Ї –Ї–∞–Ї —Н—В–Њ –≤–њ–µ—А–≤—Л–µ –±—Л–ї–Њ –Є–Љ –њ—А–Њ–і–µ–ї–∞–љ–Њ
–≤ "–Э–µ–њ—А–µ—А—Л–≤–љ–Њ–Љ –њ–µ—А–µ—Е–Њ–і–µ..." –і–ї—П —З–∞—Б—В–љ–Њ–≥–Њ —Б–ї—Г—З–∞—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–≥–Њ
–Њ—Б—Ж–Є–ї—П—В–Њ—А–∞. –Ю—Б–љ–Њ–≤–љ—Л–µ —А–∞–±–Њ—В—Л –≠.–®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–µ—А–µ–≤–µ–і–µ–љ—Л –љ–∞ —А—Г—Б—Б–Ї–Є–є —П–Ј—Л–Ї –Є
–Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ—Л –≤ –і–≤—Г—Е —Б–±–Њ—А–љ–Є–Ї–∞—Е [5,6]. –Я–Њ–Љ–Є–Љ–Њ —Н—В–Њ–≥–Њ, –Є—Е
–і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ–Њ–і—А–Њ–±–љ—Л–є –њ–µ—А–µ—Б–Ї–∞–Ј –і–∞–љ –≤ –Ї–љ–Є–≥–µ –Р.–Ш.–Р–љ—Б–µ–ї—М–Љ–∞ [7].
–†–∞–±–Њ—В—Л –®—А–µ–і–Є–љ–≥–µ—А–∞ —П–≤–ї—П—О—В—Б—П –≤–µ–љ—Ж–Њ–Љ –≤—В–Њ—А–Њ–≥–Њ –њ–Њ–і—Е–Њ–і–∞ –Ї –њ–Њ—Б—В—А–Њ–µ–љ–Є—О
–Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є, –Ї–Њ—В–Њ—А—Л–є —Г—Б–ї–Њ–≤–љ–Њ –Љ–Њ–ґ–љ–Њ –≤–µ—Б—В–Є –Њ—В –Ь–∞–Ї—Б–∞ –Я–ї–∞–љ–Ї–∞ –Є
–Р–ї—М–±–µ—А—В–∞ –≠–є–љ—И—В–µ–є–љ–∞ —З–µ—А–µ–Ј —Д–Є–≥—Г—А—Г –Ы—Г–Є –і–µ –С—А–Њ–є–ї—П –Ї –≠—А–≤–Є–љ—Г
–®—А–µ–і–Є–љ–≥–µ—А—Г. –Х—Б–ї–Є —Д–Є–Ј–Є–Ї–Є "–±–Њ—А–Њ–≤—Б–Ї–Њ–≥–Њ —В–Њ–ї–Ї–∞" –≤—Б–ї–µ–і –Ј–∞ —Б–≤–Њ–Є–Љ —Г—З–Є—В–µ–ї–µ–Љ,
–њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Н—В–Њ–≥–Њ —В—А–µ–±–Њ–≤–∞–ї–Є —А–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤, —Б–Љ–µ–ї–Њ —Г—Е–Њ–і–Є–ї–Є
–Њ—В –±–µ—А–µ–≥–Њ–≤ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є –≤ —В–∞–Є–љ—Б—В–≤–µ–љ–љ–Њ–µ –Љ–∞—В—А–Є—З–љ–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–µ –Љ–Њ—А–µ,
—В–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ–і—Е–Њ–і–∞ —Б–ї–Њ–≤–љ–Њ –≥—А–µ—З–µ—Б–Ї–Є–µ –Љ–Њ—А–µ–њ–ї–∞–≤–∞—В–µ–ї–Є
–њ—А–Њ–±–Є—А–∞–ї–Є—Б—М –≤ –љ–µ–Ј–љ–∞–Ї–Њ–Љ—Л–µ –Ј–µ–Љ–ї–Є –≤–љ—Г—В—А–Є–∞—В–Њ–Љ–љ—Л—Е —П–≤–ї–µ–љ–Є–є –љ–Є –љ–∞
—Б–µ–Ї—Г–љ–і—Г –љ–µ —Г–њ—Г—Б–Ї–∞—П –Є–Ј –≤–Є–і–∞ —Б–њ–∞—Б–Є—В–µ–ї—М–љ—Л–є –±–µ—А–µ–≥ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є.
–Х—Б–ї–Є "–±–Њ—А–Њ–≤—Ж—Л" –і–µ–ї–∞–ї–Є —Г–њ–Њ—А –љ–∞ –Ї–Њ—А–њ—Г—Б–Ї—Г–ї—Л –Є –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Б–Ї–∞—З–Ї–Є, —В–Њ
"—Н–є–љ—И—В–µ–љ–Є–∞–љ—Ж—Л" (–±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М –Є—Е —В–∞–Ї, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Ј—А–Є–Љ–Њ–µ –Є–ї–Є –љ–µ–Ј—А–Є–Љ–Њ–µ
–њ—А–Є—Б—Г—В—Б—В–≤–Є–µ –≠–є–љ—И—В–µ–є–љ–∞ —Б–≤—П–Ј—Л–≤–∞–ї–Њ –Є—Е –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є) –љ–∞ –њ–ї–∞–≤–љ—Л–µ –њ–µ—А–µ—Е–Њ–і—Л –Є
–≤–Њ–ї–љ–Њ–≤—Г—О –њ—А–Є—А–Њ–і—Г –Љ–Є–Ї—А–Њ–Љ–Є—А–∞. –Х—Б–ї–Є –С–Њ—А, –С–Њ—А–љ, –У–µ–є–Ј–µ–љ–±–µ—А–≥, –Я–∞—Г–ї–Є –Є –Ш–Њ—А–і–∞–љ
—Е–Њ—А–Њ—И–Њ –Ј–љ–∞–ї–Є –і—А—Г–≥ –і—А—Г–≥–∞ –Є —Б–Њ–Ј–і–∞–≤–∞–ї–Є –Љ–∞—В—А–Є—З–љ—Г—О –Љ–µ—Е–∞–љ–Є–Ї—Г –≤ –∞—В–Љ–Њ—Б—Д–µ—А–µ
–љ–µ–њ—А–µ—А—Л–≤–љ–Њ–≥–Њ –Њ–±—Й–µ–љ–Є—П –Є –Њ–±–Љ–µ–љ–∞ –Є–і–µ—П–Љ–Є, —В–Њ –Я–ї–∞–љ–Ї, –≠–є–љ—И—В–µ–є–љ,
–і–µ –С—А–Њ–є–ї—М –Є –®—А–µ–і–Є–љ–≥–µ—А –Њ—Б—В–∞–≤–∞–ї–Є—Б—М —В–∞–ї–∞–љ—В–ї–Є–≤—Л–Љ–Є –Њ–і–Є–љ–Њ—З–Ї–∞–Љ–Є, –∞ –Є—Е –ї–Є—З–љ–Њ–µ
–Ј–љ–∞–Ї–Њ–Љ—Б—В–≤–Њ —Б–Њ—Б—В–Њ—П–ї–Њ—Б—М —Г–ґ–µ –њ–Њ—Б–ї–µ —В–Њ–≥–Њ, –Ї–∞–Ї –≤–Њ–ї–љ–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –±—Л–ї–∞ —Б–Њ–Ј–і–∞–љ–∞.
–Ш –µ—Б–ї–Є –Љ–∞—В—А–Є—З–љ—Г—О –Љ–µ—Е–∞–љ–Є–Ї—Г –ї–Њ–≥–Є—З–µ—Б–Ї–Є –±–µ–Ј—Г–Ї–Њ—А–Є–Ј–љ–µ–љ–љ—Г—О –Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є
–±–µ–Ј—Г–њ—А–µ—З–љ—Г—О –±–Њ–ї–µ–µ —З–µ–Љ –љ–∞—Б—В–Њ—А–Њ–ґ–µ–љ–љ–Њ –≤—Б—В—А–µ—В–Є–ї–Є –≤ —И–Є—А–Њ–Ї–Є—Е –Ї—А—Г–≥–∞—Е —Д–Є–Ј–Є–Ї–Њ–≤, —В–Њ
–≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –Њ–Ї–∞–Ј–∞–ї–Є —Б–∞–Љ—Л–є –≤–Њ—Б—В–Њ—А–ґ–µ–љ–љ—Л–є –њ—А–Є–µ–Љ, –љ–∞—З–Є–љ–∞—П —Г–ґ–µ —Б —Б–∞–Љ–Њ–є
–њ–µ—А–≤–Њ–є –ї–Њ–≥–Є—З–µ—Б–Ї–Є –≤–µ—Б—М–Љ–∞ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–≤–Њ–є –Є —Б—В—А–∞–љ–љ–Њ–є —Б—В–∞—В—М–Є –®—А–µ–і–Є–љ–≥–µ—А–∞.
–° –≤—Л—Б–Њ—В—Л —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–≥–Њ –њ–Њ–љ–Є–Љ–∞–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤
–Љ–Њ–ґ–љ–Њ —Г—В–≤–µ—А–ґ–і–∞—В—М, —З—В–Њ –Њ–±–∞ –њ–Њ–і—Е–Њ–і–∞ "–±–Њ—А–Њ–≤—Б–Ї–Є–є" –Є "—Н–є–љ—И—В–µ–є–љ–Њ–≤—Б–Ї–Є–є"
–≤–љ–µ—Б–ї–Є –њ—А–Є–Љ–µ—А–љ–Њ —А–∞–≤–љ—Л–є –≤–Ї–ї–∞–і –≤ —Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Э–Њ,
–Ї–∞–Ї —Н—В–Њ –љ–µ —Б—В—А–∞–љ–љ–Њ, —Д–Њ—А–Љ–∞–ї—М–љ—Л–є –Љ–∞—В—А–Є—З–љ—Л–є –њ–Њ–і—Е–Њ–і –≤ –Ї–Њ–љ–µ—З–љ–Њ–Љ –Є—В–Њ–≥–µ
—Б–Њ–і–µ–є—Б—В–≤–Њ–≤–∞–ї –Є–Љ–µ–љ–љ–Њ –±–Њ–ї—М—И–µ–Љ—Г –њ—А–Њ–≥—А–µ—Б—Б—Г –≤ –њ–Њ–љ–Є–Љ–∞–љ–Є–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Њ–і–µ—А–ґ–∞–љ–Є—П
–Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є, –∞ –Є–љ—В—Г–Є—В–Є–≤–Є—Б—В—Б–Ї–Є–µ –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є
—П–≤–ї—П—О—В—Б—П –Њ—Б–љ–Њ–≤–Њ–є –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤—Б–µ—Е –≤—Л—З–Є—Б–ї–Є—В–µ–ї—М–љ—Л—Е –і–Њ—Б—В–Є–ґ–µ–љ–Є–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є
—Д–Є–Ј–Є–Ї–Є. –°—Г–Љ–Љ–Є—А—Г—П –≤—Б–µ –≤—Л—И–µ–Є–Ј–ї–Њ–ґ–µ–љ–љ–Њ–µ, –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ –Њ–±–∞ –њ—Г—В–Є —Б–Њ–Ј–і–∞–љ–Є—П
–Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є —П–≤–ї—П—О—В—Б—П –Ї–∞–Ї –±—Л –≤–Ј–∞–Є–Љ–љ–Њ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–Љ–Є –і—А—Г–≥ –Ї –і—А—Г–≥—Г
–≤ —В–Њ–Љ —Б–Љ—Л—Б–ї–µ, –Ї–Њ—В–Њ—А—Л–є –≤–Ї–ї–∞–і—Л–≤–∞–ї –≤ —Н—В–Њ –њ–Њ–љ—П—В–Є–µ –Э.–С–Њ—А.
–Я—А–Є —Б–Њ–Ј–і–∞–љ–Є–Є –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –У–µ–є–Ј–µ–љ–±–µ—А–≥ –Є –С–Њ—А–љ –Њ–±—А–∞—В–Є–ї–Є—Б—М –Ј–∞ –њ–Њ–Љ–Њ—Й—М—О
–Ї –Ф.–У–Є–ї—М–±–µ—А—В—Г, —З—В–Њ–±—Л —В–Њ—В —А–∞–Ј—К—П—Б–љ–Є–ї –Є–Љ –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л–µ –≤–Њ–њ—А–Њ—Б—Л
–Љ–∞—В—А–Є—З–љ–Њ–≥–Њ –Є—Б—З–Є—Б–ї–µ–љ–Є—П. –У–Є–ї—М–±–µ—А—В –њ–Њ–Љ–Њ–≥ –≥–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Є–Љ —Д–Є–Ј–Є–Ї–∞–Љ –Є –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ
–Њ–±—А–∞—В–Є–ї –Є—Е –≤–љ–Є–Љ–∞–љ–Є–µ –љ–∞ —В–Њ, —З—В–Њ –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ –Љ–∞—В—А–Є—Ж—Л –Њ–±—Л—З–љ–Њ –≤–Њ–Ј–љ–Є–Ї–∞—О—В –њ—А–Є
—А–µ—И–µ–љ–Є–Є –Ї—А–∞–µ–≤—Л—Е –Ј–∞–і–∞—З —В–µ–Њ—А–Є–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ, —З—В–Њ
–µ—Б–ї–Є –±—Л –У–µ–є–Ј–µ–љ–±–µ—А–≥ –Є –С–Њ—А–љ –њ—А–Є—Б–ї—Г—И–∞–ї–Є—Б—М –Ї —Н—В–Њ–Љ—Г –Љ—Г–і—А–Њ–Љ—Г —Б–Њ–≤–µ—В—Г, —В–Њ —Г –љ–Є—Е
–±—Л –њ–Њ—П–≤–Є–ї—Б—П —И–∞–љ—Б —А–∞–љ—М—И–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ—Б—В—А–Њ–Є—В—М –≤–Њ–ї–љ–Њ–≤—Г—О –Љ–µ—Е–∞–љ–Є–Ї—Г.
–Ч–∞–Љ–µ—З–∞–љ–Є–µ –У–Є–ї—М–±–µ—А—В–∞ –±—Л–ї–Њ –Њ—В–љ—О–і—М –љ–µ —Б–ї—Г—З–∞–є–љ—Л–Љ. –Т —В–Њ –≤—А–µ–Љ—П —А–∞–Ј–ї–Є—З–љ—Л–µ –ї–Є–љ–µ–є–љ—Л–µ
–Є –љ–µ–ї–Є–љ–µ–є–љ—Л–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П —Б–Њ—Б—В–∞–≤–ї—П–ї–Є –Њ—Б–љ–Њ–≤—Г –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ
–∞–њ–њ–∞—А–∞—В–∞ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є. –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞, —В–µ–Њ—А–Є—П —В–µ–њ–ї–Њ—В—Л,
—В–µ–Њ—А–Є—П –Ї–Њ–ї–µ–±–∞–љ–Є–є, —Н–ї–µ–Ї—В—А–Њ–і–Є–љ–∞–Љ–Є–Ї–∞ –Є –і–∞–ґ–µ —В–µ–Њ—А–Є—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є - –≤—Б–µ
–Њ–љ–Є –±–∞–Ј–Є—А–Њ–≤–∞–ї–Є—Б—М –љ–∞ –њ–Њ–ї—Г—З–µ–љ–Є–Є –Є —А–µ—И–µ–љ–Є–Є (—В–Њ—З–љ–Њ–Љ –Є–ї–Є –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ–Љ)
—А–∞–Ј–ї–Є—З–љ—Л—Е —В–Є–њ–Њ–≤ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –Ы—М–≤–Є–љ–∞—П –і–Њ–ї—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–≤
–љ–∞—З–Є–љ–∞—П –≥–і–µ-—В–Њ —Б —Б–µ—А–µ–і–Є–љ—Л XIX –≤–µ–Ї–∞ –Ј–∞–љ–Є–Љ–∞–ї–∞—Б—М —Б–Њ–Ј–і–∞–љ–Є–µ–Љ –Љ–µ—В–Њ–і–Њ–≤ —А–µ—И–µ–љ–Є—П
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –Є –Є–Ј—Г—З–µ–љ–Є–µ–Љ —Б–≤–Њ–є—Б—В–≤ –њ–Њ–ї—Г—З–Є–≤—И–Є—Е—Б—П
—А–µ—И–µ–љ–Є–є. –Ф–∞–ґ–µ –Њ–±—Й–∞—П —В–µ–Њ—А–Є—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є —Б –µ–µ —В–µ–љ–Ј–Њ—А–љ—Л–Љ –∞–њ–њ–∞—А–∞—В–Њ–Љ –≤
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –†–Є–Љ–∞–љ–∞ —Г–і–Њ–±–љ–Њ —Г–Ї–ї–∞–і—Л–≤–∞–ї–∞—Б—М –≤ –њ—А–Є–≤—Л—З–љ—Г—О —Б—Е–µ–Љ—Г, –њ—А–Є–≤–Њ–і—П —В–Њ–ї—М–Ї–Њ
–Ї —Г—Б–ї–Њ–ґ–љ–µ–љ–Є—О –≤—Л—З–Є—Б–ї–µ–љ–Є–є, –љ–Њ –љ–µ –Ї –њ–µ—А–µ–Њ—Ж–µ–љ–Ї–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–Њ–є —А–Њ–ї–Є
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –≤ –Є–Ј—Г—З–µ–љ–Є–Є –њ—А–Є—А–Њ–і—Л. –Ш —В—Г—В –≥—А—П–љ—Г–ї–∞ –Љ–∞—В—А–Є—З–љ–∞—П
–Љ–µ—Е–∞–љ–Є–Ї–∞: –Ї–Њ–Љ–Љ—Г—В–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П, –і–Є–∞–≥–Њ–љ–∞–ї–Є–Ј–∞—Ж–Є—П –Љ–∞—В—А–Є—Ж, —Г–љ–Є—В–∞—А–љ—Л–µ
–њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П. –Э–Є—З–µ–≥–Њ –Њ–±—Й–µ–≥–Њ —Б –њ—А–Є–≤—Л—З–љ–Њ–є —Б—Е–µ–Љ–Њ–є. –£–і–∞—А, —И–Њ–Ї, –њ—Г—Б—В—М –і–∞–ґ–µ
–љ–µ –≤–њ–Њ–ї–љ–µ –Њ—Б–Њ–Ј–љ–∞–љ—Л–є –Є —Б—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞–љ–љ—Л–є, –і–∞ –µ—Й–µ –њ–Њ–Љ–љ–Њ–ґ–µ–љ–љ—Л–є –љ–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М
–Њ—Б–≤–∞–Є–≤–∞—В—М –≤—Б–µ –њ—А–Є–Љ—Г–і—А–Њ—Б—В–Є –Љ–∞—В—А–Є—З–љ–Њ–≥–Њ –Є—Б—З–Є—Б–ї–µ–љ–Є—П! –Я–Њ—Н—В–Њ–Љ—Г, –Ї–Њ–≥–і–∞ –≤–і—А—Г–≥
–њ–Њ—П–≤–ї—П–µ—В—Б—П —Б—В–∞—В—М—П, –≤ –Ї–Њ—В–Њ—А–Њ–є —Г–≤–∞–ґ–∞–µ–Љ—Л–є –Є –Є–Ј–≤–µ—Б—В–љ—Л–є –њ—А–Њ—Д–µ—Б—Б–Њ—А –¶—О—А–Є—Е—Б–Ї–Њ–≥–Њ
—Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ –≠—А–≤–Є–љ –®—А–µ–і–Є–љ–≥–µ—А, –Ј–∞—А–µ–Ї–Њ–Љ–µ–љ–і–Њ–≤–∞–≤—И–Є–є —Б–µ–±—П —А—П–і–Њ–Љ –≤–µ—Б—М–Љ–∞
–Ј–∞–Љ–µ—В–љ—Л—Е —А–∞–±–Њ—В –≤ –Њ–±–ї–∞—Б—В–Є –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –≥–∞–Ј–Њ–≤, —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–Є, —Д–Є–Ј–Є–Ї–Є –љ–µ–њ—А–µ—А—Л–≤–љ—Л—Е —Б—А–µ–і, —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –Њ–њ—В–Є–Ї–Є –Є –Њ–±—Й–µ–є —В–µ–Њ—А–Є–Є
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ—Б—В–Є (–њ–Њ—Б–ї–µ–і–љ–Є–µ –Ј–∞—Б–ї—Г–ґ–Є–ї–Є –≤–µ—Б—М–Љ–∞ –≤—Л—Б–Њ–Ї—Г—О –Њ—Ж–µ–љ–Ї—Г –Р.–≠–є–љ—И—В–µ–є–љ–∞),
–њ–Є—И–µ—В —А–∞–±–Њ—В—Г, –≤ –Ї–Њ—В–Њ—А–Њ–є —Б –њ–µ—А–≤—Л—Е —Б—В—А–Њ—З–µ–Ї —Г—В–≤–µ—А–ґ–і–∞–µ—В, —З—В–Њ –≤ –љ–µ–є –Њ–љ
"... —Б–Њ–±–Є—А–∞–µ—В—Б—П –њ–Њ–Ї–∞–Ј–∞—В—М –љ–∞ –њ—А–Њ—Б—В–µ–є—И–µ–Љ –њ—А–Є–Љ–µ—А–µ –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Њ–≥–Њ
—Б–≤–Њ–±–Њ–і–љ–Њ–≥–Њ –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞, —З—В–Њ –Њ–±—Л—З–љ—Л–µ –њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –Љ–Њ–≥—Г—В
–±—Л—В—М –Ј–∞–Љ–µ–љ–µ–љ—Л –і—А—Г–≥–Є–Љ–Є –њ–Њ–ї–Њ–ґ–µ–љ–Є—П–Љ–Є, –≤ –Ї–Њ—В–Њ—А—Л—Е —Г–ґ–µ –љ–µ –≤–≤–Њ–і–Є—В—Б—П –Ї–∞–Ї–Є—Е-–ї–Є–±–Њ
"—Ж–µ–ї—Л—Е —З–Є—Б–µ–ї", —З—В–Њ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В—М "–њ–Њ–ї—Г—З–∞–µ—В—Б—П –њ—А–Є —Н—В–Њ–Љ –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Л–Љ
–Њ–±—А–∞–Ј–Њ–Љ —Б–∞–Љ–∞ –њ–Њ —Б–µ–±–µ –њ–Њ–і–Њ–±–љ–Њ —В–Њ–Љ—Г, –Ї–∞–Ї —Б–∞–Љ–∞ –њ–Њ —Б–µ–±–µ –њ–Њ–ї—Г—З–∞–µ—В—Б—П
—Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В—М —З–Є—Б–ї–∞ —Г–Ј–ї–Њ–≤ –њ—А–Є —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–Є –Ї–Њ–ї–µ–±–ї—О—Й–µ–є—Б—П —Б—В—А—Г–љ—Л
(–≤–Њ—В, –≤–Њ—В –Њ–љ–∞ - —В–∞–Ї–∞—П –і–Њ–ї–≥–Њ–ґ–і–∞–љ–љ–∞—П –∞–љ–∞–ї–Њ–≥–Є—П —Б –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є
—Д–Є–Ј–Є–Ї–Њ–є! - –Э.–Э.)", —З—В–Њ —Н—В–Њ "–љ–Њ–≤–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–±–Њ–±—Й–µ–љ–Њ"
–Є "—З—В–Њ –Њ–љ–Њ —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ–Њ —Б –Ш–°–Ґ–Ш–Э–Э–Ю–Щ –Я–†–Ш–†–Ю–Ф–Ю–Щ –Ъ–Т–Р–Э–Ґ–Ю–Т–Р–Э–Ш–ѓ", —В–Њ –ї—О–±–Њ–Љ—Г
"–Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г" —Д–Є–Ј–Є–Ї—Г —Б —А–∞–і–Њ—Б—В—М—О —Е–Њ—З–µ—В—Б—П –≤–µ—А–Є—В—М –≤ –њ–Њ–і–Њ–±–љ—Л–µ –Ј–∞–≤–µ—А–µ–љ–Є—П
–Љ–∞—Б—В–Є—В–Њ–≥–Њ –њ—А–Њ—Д–µ—Б—Б–Њ—А–∞.
–Я—А–µ–ґ–і–µ, —З–µ–Љ –Є–і—В–Є –і–∞–ї—М—И–µ, —А–∞–Ј–±–µ—А–µ–Љ, —З—В–Њ –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–ї
–њ–Њ–і "–Њ–±—Л—З–љ—Л–Љ–Є –њ—А–∞–≤–Є–ї–∞–Љ–Є –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П". –Ъ–∞–Ј–∞–ї–Њ—Б—М –±—Л, —З—В–Њ –Є–Ј
–≤—Б–µ–≥–Њ –≤—Л—И–µ—Б–Ї–∞–Ј–∞–љ–љ–Њ–≥–Њ –Њ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ —Б –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М—О —Б–ї–µ–і—Г–µ—В,
—З—В–Њ –њ–Њ–і "–Њ–±—Л—З–љ—Л–Љ–Є –њ—А–∞–≤–Є–ї–∞–Љ–Є" –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–љ–Є–Љ–∞–µ—В –њ—А–∞–≤–Є–ї–∞ –і–ї—П
–љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є –Љ–∞—В—А–Є—Ж—Л –У–∞–Љ–Є–ї—М—В–Њ–љ–∞ –≤ —В–µ–Њ—А–Є–Є
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞. –Э–Њ –µ—Б–ї–Є –і–∞–ґ–µ –і–ї—П —Б–∞–Љ–Є—Е –∞–≤—В–Њ—А–Њ–≤ –Љ–∞—В—А–Є—З–љ–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–Є –і–∞–љ–љ—Л–µ –њ—А–∞–≤–Є–ї–∞ —Б–ї–Њ–ґ–љ—Л –Є –љ–µ–њ—А–Є–≤—Л—З–љ—Л, –µ—Б–ї–Є –њ—А–Є –Є—Е –њ—А–Є–Љ–µ–љ–µ–љ–Є–Є
–С–Њ—А–љ, –У–µ–є–Ј–µ–љ–±–µ—А–≥ –Є –Ш–Њ—А–і–∞–љ –≤—Л–љ—Г–ґ–і–µ–љ—Л –Ї–Њ–љ—Б—Г–ї—М—В–Є—А–Њ–≤–∞—В—М—Б—П —Б
–Ї—А—Г–њ–љ–µ–є—И–Є–Љ–Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞–Љ–Є —Б–≤–Њ–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є, —В–Њ —Б –Ї–∞–Ї–Њ–є —Б—В–∞—В–Є –љ–Њ–≤—Л–µ –њ—А–∞–≤–Є–ї–∞
–Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –≤–і—А—Г–≥ —Б—В–∞–љ–Њ–≤—П—В—Б—П "–Њ–±—Л—З–љ—Л–Љ–Є" –і–ї—П —Г—З–µ–љ–Њ–≥–Њ, –≤–µ—Б—М–Љ–∞ –і–∞–ї–µ–Ї–Њ–≥–Њ –Њ—В
–њ—А–Њ–њ–Њ–≤–µ–і–љ–Є–Ї–Њ–≤ –љ–Њ–≤–Њ–є "–≥–µ—В—В–Є–љ–≥–µ–љ—Б–Ї–Њ–є —Г—З–µ–љ–Њ—Б—В–Є" –Є —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ –љ–µ –Ј–љ–∞–Ї–Њ–Љ–Њ–≥–Њ
—Б —Д–Є–ї–Њ—Б–Њ—Д—Б–Ї–Є–Љ–Є –Є –Љ–µ—В–Њ–і–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–Љ–Є –≤–Ј–≥–ї—П–і–∞–Љ–Є –Э.–С–Њ—А–∞, –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –≤—Л—А–Њ—Б
—Д–Њ—А–Љ–∞–ї–Є–Ј–Љ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є? –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ–µ—А–≤–Њ–µ "–Њ—З–µ–≤–Є–і–љ–Њ–µ"
–њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –љ–µ –≤–µ—А–љ–Њ. –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –Ї –Љ–Њ–Љ–µ–љ—В—Г –љ–∞–њ–Є—Б–∞–љ–Є—П —Б–≤–Њ–µ–є
—Б—В–∞—В—М–Є –®—А–µ–і–Є–љ–≥–µ—А –Љ–Њ–≥, —А–∞–Ј–≤–µ —З—В–Њ, –Ј–љ–∞—В—М –Њ —Б–∞–Љ–Њ–є
–њ–µ—А–≤–Њ–є —А–∞–±–Њ—В–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –Ї–Њ—В–Њ—А–∞—П, —Е–Њ—В—П –Є –њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О
"Zeitschrift f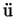 r Physik" –µ—Й–µ 29 –Є—О–ї—П, –љ–Њ –±—Л–ї–∞ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–∞
—В–Њ–ї—М–Ї–Њ –≤ –Ї–Њ–љ—Ж–µ –≥–Њ–і–∞ (–≤—Б–µ, –Ї—В–Њ –Є–Љ–µ–ї –і–µ–ї–Њ —Б –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П–Љ–Є —Б–≤–Њ–Є—Е –љ–∞—Г—З–љ—Л—Е
—Б—В–∞—В–µ–є, –Љ–Њ–≥—Г—В –њ–Њ–і—В–≤–µ—А–і–Є—В—М, —З—В–Њ —В–∞–Ї–∞—П –Ј–∞–і–µ—А–ґ–Ї–∞ –≤–њ–Њ–ї–љ–µ –Њ–±—Л—З–љ–∞: –њ–Њ–Ї–∞
–Њ—В—А–µ—Ж–µ–Ј–Є—А—Г—О—В, –њ–Њ–Ї–∞ –љ–∞–±–µ—А—Г—В, –њ–Њ–Ї–∞ –≥—А–∞–љ–Ї–Є –њ—А–Є—И–ї—О—В, –њ–Њ–Ї–∞ –Њ—В–њ–µ—З–∞—В–∞—О—В,
–Є–Љ–µ–љ–љ–Њ –њ–Њ—Н—В–Њ–Љ—Г –≤ –≤–Њ–њ—А–Њ—Б–∞—Е –њ—А–Є–Њ—А–Є—В–µ—В–∞ –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –Є–≥—А–∞–µ—В —В–Њ, –Ї–Њ–≥–і–∞
—Б—В–∞—В—М—П –њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О, –∞ –љ–µ –Ї–Њ–≥–і–∞ –±—Л–ї–∞ –љ–∞–њ–µ—З–∞—В–∞–љ–∞), –∞ –і–≤–µ
—Б—В–∞—В—М–Є, –≤ –Ї–Њ—В–Њ—А—Л—Е –Љ–∞—В—А–Є—З–љ–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ —Д–Њ—А–Љ—Г–ї–Є—А—Г–µ—В—Б—П —Б—В—А–Њ–≥–Њ [3],
–і–∞–ґ–µ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є –®—А–µ–і–Є–љ–≥–µ—А—Г –Є–Ј–≤–µ—Б—В–љ—Л –±—Л—В—М –љ–µ –Љ–Њ–≥–ї–Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤—Л—И–ї–Є
–Є–Ј –њ–µ—З–∞—В–Є –≤ –њ–µ—А–≤–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ 1926 –≥–Њ–і–∞, —В–Њ –µ—Б—В—М —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ –Њ—Б–љ–Њ–≤–∞ –≤–Њ–ї–љ–Њ–≤–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–Є —Г–ґ–µ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–∞. –Т—Б–≤—П–Ј–Є —Б —Н—В–Є–Љ –љ–∞–Љ –Ї–∞–ґ–µ—В—Б—П –љ–µ–њ—А–∞–≤–Є–ї—М–љ—Л–Љ
—Б–ї–µ–і—Г—О—Й–µ–µ –Ј–∞–Љ–µ—З–∞–љ–Є–µ –∞–≤—В–Њ—А–Њ–≤ –љ–µ–і–∞–≤–љ–Њ –≤—Л—И–µ–і—И–µ–є –Ї–љ–Є–≥–Є [8] –љ–∞
—Б—В—А. 59: "–Ь–Њ–ґ–љ–Њ –і—Г–Љ–∞—В—М, –®—А–µ–і–Є–љ–≥–µ—А –Є—Б–Ї—А–µ–љ–љ–µ —Б—З–Є—В–∞–ї, —З—В–Њ –Њ–љ —Б–Њ–Ј–і–∞–ї –љ–Њ–≤—Г—О
—В–µ–Њ—А–Є—О –∞—В–Њ–Љ–љ—Л—Е —П–≤–ї–µ–љ–Є–є. –Т–Њ –≤—Б—П–Ї–Њ–Љ —Б–ї—Г—З–∞–µ —Н—В–Њ –≤–њ–Њ–ї–љ–µ –Њ–±—К—П—Б–љ—П–µ—В —Г–њ–Њ—А–љ–Њ–µ
–љ–µ–ґ–µ–ї–∞–љ–Є–µ –Ј–∞–Љ–µ—З–∞—В—М –њ—А–µ–і—И–µ—Б—В–≤–µ–љ–љ–Є–Ї–Њ–≤. –Т –µ–≥–Њ —Б—В–∞—В—М–µ –љ–µ—В —Б—Б—Л–ї–Њ–Ї –љ–∞
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –С–Њ—А–љ–∞ –Є –Ш–Њ—А–і–∞–љ–∞, –Є –і–∞–ґ–µ –Я–∞—Г–ї–Є, –Ї–Њ—В–Њ—А—Л–є —Г–ґ–µ —А–µ—И–Є–ї –Ј–∞–і–∞—З—Г
–Ъ–µ–њ–ї–µ—А–∞". –Ф–∞ –Є—Е –Є –љ–µ –Љ–Њ–≥–ї–Њ –±—Л—В—М! –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –њ–Њ—Б–ї–µ —Б–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є—П –і–∞—В –љ–µ
–≤—Л–Ј—Л–≤–∞–µ—В –љ–Є–Ї–∞–Ї–Њ–≥–Њ —Б–Њ–Љ–љ–µ–љ–Є—П, —З—В–Њ —Б—В–∞—В—М—П –Я–∞—Г–ї–Є –њ–Њ—П–≤–Є–ї–∞—Б—М –≤ —А–µ–і–∞–Ї—Ж–Є–Є
"Zeitschrift..." —Г–ґ–µ –Я–Ю–°–Ы–Х —В–Њ–≥–Њ, –Ї–∞–Ї —Б—В–∞—В—М—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –±—Л–ї–∞ –њ–Њ—Б–ї–∞–љ–∞
–≤ "Annalen ...". –Р –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ—Л –Њ–±–µ –≤–Њ–Њ–±—Й–µ –≤–Њ –≤—В–Њ—А–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ 1926
–≥–Њ–і–∞. –Ъ—Б—В–∞—В–Є, —Б—Б—Л–ї–Ї–Є –љ–∞ —А–∞–±–Њ—В—Л –њ–Њ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –њ–Њ—П–≤–ї—П—О—В—Б—П —Г–ґ–µ
–≤–Њ –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–µ –®—А–µ–і–Є–љ–≥–µ—А–∞, –∞ —З–µ—В–≤–µ—А—В–∞—П –њ–Њ —Б—З–µ—В—Г –µ–≥–Њ —А–∞–±–Њ—В–∞ —Ж–µ–ї–Є–Ї–Њ–Љ
–њ–Њ—Б–≤—П—Й–µ–љ–∞ –њ–Њ–Є—Б–Ї—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є—П –Љ–µ–ґ–і—Г –Љ–∞—В—А–Є—З–љ–Њ–є –Є –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–∞–Љ–Є.
–Ь–Њ–ґ–љ–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і, –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤–Њ –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–µ
–®—А–µ–і–Є–љ–≥–µ—А –±–ї–∞–≥–Њ–і–∞—А–Є—В –Ј–∞ "–і—А—Г–ґ–µ—Б–Ї–Њ–µ –њ–Є—Б—М–Љ–Њ" —Б –њ–Њ–ї–µ–Ј–љ–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–µ–є,
—Б–Њ–Њ–±—Й–Є–ї –®—А–µ–і–Є–љ–≥–µ—А—Г –Њ –і–Њ—Б—В–Є–ґ–µ–љ–Є—П—Е –≥–µ—В—В–Є–љ–≥–µ–љ—Ж–µ–≤. –І—В–Њ–±—Л –Ј–∞–Ї—А—Л—В—М
—В–µ–Љ—Г, –Њ—В–Љ–µ—З—Г, —З—В–Њ –≤ —Ж–µ–ї–Њ–Љ –≤ –Њ—З–µ–љ—М —Е–Њ—А–Њ—И–µ–є –Є —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Ї–љ–Є–≥–µ
[8] –∞–≤—В–Њ—А—Л —П–≤–љ–Њ —Б–Є–Љ–њ–∞—В–Є–Ј–Є—А—Г—О—В –У–µ–є–Ј–µ–љ–±–µ—А–≥—Г –Є —Д–Њ–љ –Э–µ–є–Љ–∞–љ—Г,
–Є—Е –≤—Л–і–∞—О—Й–Є–Љ—Б—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П–Љ –Є, –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, –≤—А–∞–ґ–і–µ–±–љ–Њ –Њ—В–љ–Њ—Б—П—В—Б—П –Ї
–љ–µ –Љ–µ–љ–µ–µ –≤–∞–ґ–љ—Л–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –®—А–µ–і–Є–љ–≥–µ—А–∞, –≤—Б—П—З–µ—Б–Ї–Є –њ—Л—В–∞—П—Б—М –њ—А–Є–љ–Є–Ј–Є—В—М
–Є—Е –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ—Б—В—М –Є –Ј–љ–∞—З–Є–Љ–Њ—Б—В—М. –Я–Њ–і–Њ–±–љ–∞—П –њ—А–µ–і–≤–Ј—П—В–Њ—Б—В—М –≤–Њ –Љ–љ–Њ–≥–Њ–Љ –њ–Њ—А—В–Є—В
–Њ–±—Й–µ–µ –≤–њ–µ—З–∞—В–ї–µ–љ–Є–µ –Њ—В –Ї–љ–Є–≥–Є.
r Physik" –µ—Й–µ 29 –Є—О–ї—П, –љ–Њ –±—Л–ї–∞ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–∞
—В–Њ–ї—М–Ї–Њ –≤ –Ї–Њ–љ—Ж–µ –≥–Њ–і–∞ (–≤—Б–µ, –Ї—В–Њ –Є–Љ–µ–ї –і–µ–ї–Њ —Б –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П–Љ–Є —Б–≤–Њ–Є—Е –љ–∞—Г—З–љ—Л—Е
—Б—В–∞—В–µ–є, –Љ–Њ–≥—Г—В –њ–Њ–і—В–≤–µ—А–і–Є—В—М, —З—В–Њ —В–∞–Ї–∞—П –Ј–∞–і–µ—А–ґ–Ї–∞ –≤–њ–Њ–ї–љ–µ –Њ–±—Л—З–љ–∞: –њ–Њ–Ї–∞
–Њ—В—А–µ—Ж–µ–Ј–Є—А—Г—О—В, –њ–Њ–Ї–∞ –љ–∞–±–µ—А—Г—В, –њ–Њ–Ї–∞ –≥—А–∞–љ–Ї–Є –њ—А–Є—И–ї—О—В, –њ–Њ–Ї–∞ –Њ—В–њ–µ—З–∞—В–∞—О—В,
–Є–Љ–µ–љ–љ–Њ –њ–Њ—Н—В–Њ–Љ—Г –≤ –≤–Њ–њ—А–Њ—Б–∞—Е –њ—А–Є–Њ—А–Є—В–µ—В–∞ –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –Є–≥—А–∞–µ—В —В–Њ, –Ї–Њ–≥–і–∞
—Б—В–∞—В—М—П –њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О, –∞ –љ–µ –Ї–Њ–≥–і–∞ –±—Л–ї–∞ –љ–∞–њ–µ—З–∞—В–∞–љ–∞), –∞ –і–≤–µ
—Б—В–∞—В—М–Є, –≤ –Ї–Њ—В–Њ—А—Л—Е –Љ–∞—В—А–Є—З–љ–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ —Д–Њ—А–Љ—Г–ї–Є—А—Г–µ—В—Б—П —Б—В—А–Њ–≥–Њ [3],
–і–∞–ґ–µ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є –®—А–µ–і–Є–љ–≥–µ—А—Г –Є–Ј–≤–µ—Б—В–љ—Л –±—Л—В—М –љ–µ –Љ–Њ–≥–ї–Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤—Л—И–ї–Є
–Є–Ј –њ–µ—З–∞—В–Є –≤ –њ–µ—А–≤–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ 1926 –≥–Њ–і–∞, —В–Њ –µ—Б—В—М —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ –Њ—Б–љ–Њ–≤–∞ –≤–Њ–ї–љ–Њ–≤–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–Є —Г–ґ–µ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–∞. –Т—Б–≤—П–Ј–Є —Б —Н—В–Є–Љ –љ–∞–Љ –Ї–∞–ґ–µ—В—Б—П –љ–µ–њ—А–∞–≤–Є–ї—М–љ—Л–Љ
—Б–ї–µ–і—Г—О—Й–µ–µ –Ј–∞–Љ–µ—З–∞–љ–Є–µ –∞–≤—В–Њ—А–Њ–≤ –љ–µ–і–∞–≤–љ–Њ –≤—Л—И–µ–і—И–µ–є –Ї–љ–Є–≥–Є [8] –љ–∞
—Б—В—А. 59: "–Ь–Њ–ґ–љ–Њ –і—Г–Љ–∞—В—М, –®—А–µ–і–Є–љ–≥–µ—А –Є—Б–Ї—А–µ–љ–љ–µ —Б—З–Є—В–∞–ї, —З—В–Њ –Њ–љ —Б–Њ–Ј–і–∞–ї –љ–Њ–≤—Г—О
—В–µ–Њ—А–Є—О –∞—В–Њ–Љ–љ—Л—Е —П–≤–ї–µ–љ–Є–є. –Т–Њ –≤—Б—П–Ї–Њ–Љ —Б–ї—Г—З–∞–µ —Н—В–Њ –≤–њ–Њ–ї–љ–µ –Њ–±—К—П—Б–љ—П–µ—В —Г–њ–Њ—А–љ–Њ–µ
–љ–µ–ґ–µ–ї–∞–љ–Є–µ –Ј–∞–Љ–µ—З–∞—В—М –њ—А–µ–і—И–µ—Б—В–≤–µ–љ–љ–Є–Ї–Њ–≤. –Т –µ–≥–Њ —Б—В–∞—В—М–µ –љ–µ—В —Б—Б—Л–ї–Њ–Ї –љ–∞
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –С–Њ—А–љ–∞ –Є –Ш–Њ—А–і–∞–љ–∞, –Є –і–∞–ґ–µ –Я–∞—Г–ї–Є, –Ї–Њ—В–Њ—А—Л–є —Г–ґ–µ —А–µ—И–Є–ї –Ј–∞–і–∞—З—Г
–Ъ–µ–њ–ї–µ—А–∞". –Ф–∞ –Є—Е –Є –љ–µ –Љ–Њ–≥–ї–Њ –±—Л—В—М! –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –њ–Њ—Б–ї–µ —Б–Њ–њ–Њ—Б—В–∞–≤–ї–µ–љ–Є—П –і–∞—В –љ–µ
–≤—Л–Ј—Л–≤–∞–µ—В –љ–Є–Ї–∞–Ї–Њ–≥–Њ —Б–Њ–Љ–љ–µ–љ–Є—П, —З—В–Њ —Б—В–∞—В—М—П –Я–∞—Г–ї–Є –њ–Њ—П–≤–Є–ї–∞—Б—М –≤ —А–µ–і–∞–Ї—Ж–Є–Є
"Zeitschrift..." —Г–ґ–µ –Я–Ю–°–Ы–Х —В–Њ–≥–Њ, –Ї–∞–Ї —Б—В–∞—В—М—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –±—Л–ї–∞ –њ–Њ—Б–ї–∞–љ–∞
–≤ "Annalen ...". –Р –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ—Л –Њ–±–µ –≤–Њ–Њ–±—Й–µ –≤–Њ –≤—В–Њ—А–Њ–є –њ–Њ–ї–Њ–≤–Є–љ–µ 1926
–≥–Њ–і–∞. –Ъ—Б—В–∞—В–Є, —Б—Б—Л–ї–Ї–Є –љ–∞ —А–∞–±–Њ—В—Л –њ–Њ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –њ–Њ—П–≤–ї—П—О—В—Б—П —Г–ґ–µ
–≤–Њ –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–µ –®—А–µ–і–Є–љ–≥–µ—А–∞, –∞ —З–µ—В–≤–µ—А—В–∞—П –њ–Њ —Б—З–µ—В—Г –µ–≥–Њ —А–∞–±–Њ—В–∞ —Ж–µ–ї–Є–Ї–Њ–Љ
–њ–Њ—Б–≤—П—Й–µ–љ–∞ –њ–Њ–Є—Б–Ї—Г —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є—П –Љ–µ–ґ–і—Г –Љ–∞—В—А–Є—З–љ–Њ–є –Є –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–∞–Љ–Є.
–Ь–Њ–ґ–љ–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і, –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤–Њ –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–µ
–®—А–µ–і–Є–љ–≥–µ—А –±–ї–∞–≥–Њ–і–∞—А–Є—В –Ј–∞ "–і—А—Г–ґ–µ—Б–Ї–Њ–µ –њ–Є—Б—М–Љ–Њ" —Б –њ–Њ–ї–µ–Ј–љ–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–µ–є,
—Б–Њ–Њ–±—Й–Є–ї –®—А–µ–і–Є–љ–≥–µ—А—Г –Њ –і–Њ—Б—В–Є–ґ–µ–љ–Є—П—Е –≥–µ—В—В–Є–љ–≥–µ–љ—Ж–µ–≤. –І—В–Њ–±—Л –Ј–∞–Ї—А—Л—В—М
—В–µ–Љ—Г, –Њ—В–Љ–µ—З—Г, —З—В–Њ –≤ —Ж–µ–ї–Њ–Љ –≤ –Њ—З–µ–љ—М —Е–Њ—А–Њ—И–µ–є –Є —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є –Ї–љ–Є–≥–µ
[8] –∞–≤—В–Њ—А—Л —П–≤–љ–Њ —Б–Є–Љ–њ–∞—В–Є–Ј–Є—А—Г—О—В –У–µ–є–Ј–µ–љ–±–µ—А–≥—Г –Є —Д–Њ–љ –Э–µ–є–Љ–∞–љ—Г,
–Є—Е –≤—Л–і–∞—О—Й–Є–Љ—Б—П –і–Њ—Б—В–Є–ґ–µ–љ–Є—П–Љ –Є, –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, –≤—А–∞–ґ–і–µ–±–љ–Њ –Њ—В–љ–Њ—Б—П—В—Б—П –Ї
–љ–µ –Љ–µ–љ–µ–µ –≤–∞–ґ–љ—Л–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –®—А–µ–і–Є–љ–≥–µ—А–∞, –≤—Б—П—З–µ—Б–Ї–Є –њ—Л—В–∞—П—Б—М –њ—А–Є–љ–Є–Ј–Є—В—М
–Є—Е –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ—Б—В—М –Є –Ј–љ–∞—З–Є–Љ–Њ—Б—В—М. –Я–Њ–і–Њ–±–љ–∞—П –њ—А–µ–і–≤–Ј—П—В–Њ—Б—В—М –≤–Њ –Љ–љ–Њ–≥–Њ–Љ –њ–Њ—А—В–Є—В
–Њ–±—Й–µ–µ –≤–њ–µ—З–∞—В–ї–µ–љ–Є–µ –Њ—В –Ї–љ–Є–≥–Є.
–Э–Њ –≤–µ—А–љ–µ–Љ—Б—П –Ї –≤–Њ–њ—А–Њ—Б—Г, —З—В–Њ –ґ–µ –њ–Њ–љ–Є–Љ–∞–ї –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–і "–Њ–±—Л—З–љ—Л–Љ–Є –њ—А–∞–≤–Є–ї–∞–Љ–Є
–Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П"? –Х—Б–ї–Є –±–Њ–ї–µ–µ –і–µ—В–∞–ї—М–љ–Њ –Њ–Ј–љ–∞–Ї–Њ–Љ–Є—В—М—Б—П —Б –Є—Б—В–Њ—А–Є–µ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є,
—В–Њ –љ–∞ –њ–Њ—Б—В–∞–≤–ї–µ–љ–љ—Л–є –≤–Њ–њ—А–Њ—Б –Љ–Њ–ґ–µ—В –њ–Њ—П–≤–Є—В—М—Б—П —В–Њ–ї—М–Ї–Њ –Њ–і–Є–љ –Њ—В–≤–µ—В. –®—А–µ–і–Є–љ–≥–µ—А
–Є–Љ–µ–ї –≤–≤–Є–і—Г (–Ї–≤–∞–Ј–Є–Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–µ) –њ—А–∞–≤–Є–ї–Њ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞
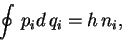 |
(1) |
–≥–і–µ 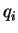 –Є
–Є 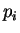 - –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е
–Є–Љ–њ—Г–ї—М—Б–Њ–≤ —Б–Є—Б—В–µ–Љ—Л,
- –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е
–Є–Љ–њ—Г–ї—М—Б–Њ–≤ —Б–Є—Б—В–µ–Љ—Л,  -–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞, –∞
-–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –Я–ї–∞–љ–Ї–∞, –∞ 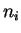 -—Ж–µ–ї—Л–µ —З–Є—Б–ї–∞.
–Ф–∞–љ–љ–Њ–µ –њ—А–∞–≤–Є–ї–Њ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –±—Л–ї–Њ –њ–Њ—Б—В—Г–ї–Є—А–Њ–≤–∞–љ–љ–Њ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–Њ–Љ –≤ 1916 –≥–Њ–і—Г
–Ї–∞–Ї –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ–µ –Њ–±–Њ–±—Й–µ–љ–Є–µ —В–µ–Њ—А–Є–Є –∞—В–Њ–Љ–∞ –С–Њ—А–∞ –Є –Ї 1925 —Б—В–∞–ї–Њ "–Њ–±—Л—З–љ—Л–Љ", –љ–Њ
—В—А–µ–±–Њ–≤–∞–љ–Є–µ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є –≤ (1)
–њ—А–Њ–і–Њ–ї–ґ–∞–ї–Њ –Њ—Б—В–∞–≤–∞—В—М—Б—П –Ј–∞–≥–∞–і–Њ—З–љ—Л–Љ –Є –љ–µ–Њ–±—К—П—Б–љ–Є–Љ—Л–Љ. –Ш–Љ–µ–љ–љ–Њ —Б —Н—В–Є–Љ –њ—А–∞–≤–Є–ї–Њ–Љ
—Б–≤—П–Ј–∞–љ—Л –≤—Б–µ —Г—Б–њ–µ—Е–Є "–љ–∞–Є–≤–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є" –і–Њ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л—Е —А–∞–±–Њ—В
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Є –®—А–µ–і–Є–љ–≥–µ—А–∞, –≤ –Ї–Њ—В–Њ—А—Л—Е —Б–Њ–і–µ—А–ґ–∞–ї–∞—Б—М –љ–Њ–≤–∞—П –Ї–≤–∞–љ—В–Њ–≤–∞—П —В–µ–Њ—А–Є—П.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –љ–Њ–≤–∞—П –Ї–≤–∞–љ—В–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –њ—А–Њ—П—Б–љ–Є–ї–∞ —Б–Љ—Л—Б–ї –њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П
–С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ –Є —Г–Ї–∞–Ј–∞–ї–∞ –љ–∞ –µ–≥–Њ –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ—Б—В—М. –Ф–ї—П –њ–Њ–ї—Г—З–µ–љ–Є—П –±–Њ–ї–µ–µ
–њ–Њ–і—А–Њ–±–љ–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Ј–∞–Є–љ—В–µ—А–µ—Б–Њ–≤–∞–љ–љ–Њ–Љ—Г —З–Є—В–∞—В–µ–ї—О –Љ–Њ–ґ–љ–Њ —А–µ–Ї–Њ–Љ–µ–љ–і–Њ–≤–∞—В—М
–Ї–љ–Є–≥–Є [7] –Є [9].
-—Ж–µ–ї—Л–µ —З–Є—Б–ї–∞.
–Ф–∞–љ–љ–Њ–µ –њ—А–∞–≤–Є–ї–Њ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –±—Л–ї–Њ –њ–Њ—Б—В—Г–ї–Є—А–Њ–≤–∞–љ–љ–Њ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–Њ–Љ –≤ 1916 –≥–Њ–і—Г
–Ї–∞–Ї –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ–µ –Њ–±–Њ–±—Й–µ–љ–Є–µ —В–µ–Њ—А–Є–Є –∞—В–Њ–Љ–∞ –С–Њ—А–∞ –Є –Ї 1925 —Б—В–∞–ї–Њ "–Њ–±—Л—З–љ—Л–Љ", –љ–Њ
—В—А–µ–±–Њ–≤–∞–љ–Є–µ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є –≤ (1)
–њ—А–Њ–і–Њ–ї–ґ–∞–ї–Њ –Њ—Б—В–∞–≤–∞—В—М—Б—П –Ј–∞–≥–∞–і–Њ—З–љ—Л–Љ –Є –љ–µ–Њ–±—К—П—Б–љ–Є–Љ—Л–Љ. –Ш–Љ–µ–љ–љ–Њ —Б —Н—В–Є–Љ –њ—А–∞–≤–Є–ї–Њ–Љ
—Б–≤—П–Ј–∞–љ—Л –≤—Б–µ —Г—Б–њ–µ—Е–Є "–љ–∞–Є–≤–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є" –і–Њ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л—Е —А–∞–±–Њ—В
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞ –Є –®—А–µ–і–Є–љ–≥–µ—А–∞, –≤ –Ї–Њ—В–Њ—А—Л—Е —Б–Њ–і–µ—А–ґ–∞–ї–∞—Б—М –љ–Њ–≤–∞—П –Ї–≤–∞–љ—В–Њ–≤–∞—П —В–µ–Њ—А–Є—П.
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –љ–Њ–≤–∞—П –Ї–≤–∞–љ—В–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ –њ—А–Њ—П—Б–љ–Є–ї–∞ —Б–Љ—Л—Б–ї –њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П
–С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ –Є —Г–Ї–∞–Ј–∞–ї–∞ –љ–∞ –µ–≥–Њ –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ—Б—В—М. –Ф–ї—П –њ–Њ–ї—Г—З–µ–љ–Є—П –±–Њ–ї–µ–µ
–њ–Њ–і—А–Њ–±–љ–Њ–є –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Ј–∞–Є–љ—В–µ—А–µ—Б–Њ–≤–∞–љ–љ–Њ–Љ—Г —З–Є—В–∞—В–µ–ї—О –Љ–Њ–ґ–љ–Њ —А–µ–Ї–Њ–Љ–µ–љ–і–Њ–≤–∞—В—М
–Ї–љ–Є–≥–Є [7] –Є [9].
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Є–Ј–љ–∞—З–∞–ї—М–љ–Њ –≤ —Б–≤–Њ–µ–є —А–∞–±–Њ—В–µ –®—А–µ–і–Є–љ–≥–µ—А –њ—Л—В–∞–ї—Б—П –њ—А–Њ—П—Б–љ–Є—В—М
—Б—Г—Й–љ–Њ—Б—В—М –њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ –Є –Є–Ј–±–∞–≤–Є—В—М—Б—П –Њ—В
–Ј–∞–≥–∞–і–Њ—З–љ–Њ–є –њ–Њ—Б—В—Г–ї–∞—В–Є–≤–љ–Њ–є —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є –Є–Љ–µ–љ–љ–Њ –≤ (1). –Э–Њ
—В–∞–Ї —Б–ї–Њ–ґ–Є–ї–Њ—Б—М, —З—В–Њ –Ј–∞ –≤—А–µ–Љ—П –Љ–µ–ґ–і—Г –љ–∞–њ–Є—Б–∞–љ–Є–µ–Љ –Є –њ—Г–±–ї–Є–Ї–∞—Ж–Є–µ–є –њ–µ—А–≤–Њ–є
—А–∞–±–Њ—В—Л –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, —Г –љ–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ—П–≤–Є–ї—Б—П
–Є–љ–Њ–є –±–Њ–ї–µ–µ –њ–Њ–і–≥–Њ—В–Њ–≤–ї–µ–љ–љ—Л–є –Є –≥—А–Њ–Ј–љ—Л–є –Њ–њ–њ–Њ–љ–µ–љ—В - —В–µ–Њ—А–Є—П
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞. –Ш–Љ–µ–љ–љ–Њ –≤ –Ї–∞—З–µ—Б—В–≤–µ "—Б–њ–∞—Б–Є—В–µ–ї—М–љ–Њ–є
–∞–ї—М—В–µ—А–љ–∞—В–Є–≤—Л –Њ—В —Г–ґ–∞—Б–Њ–≤ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є" –≤–Њ–ї–љ–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞
–®—А–µ–і–Є–љ–≥–µ—А–∞ –Є –±—Л–ї–∞ –≤–Њ—Б–њ—А–Є–љ—П—В–∞ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Є–Ї–∞–Љ–Є.
–Э–∞–Ї–Њ–љ–µ—Ж –њ–µ—А–µ–є–і–µ–Љ –Ї —А–∞–Ј–±–Њ—А—Г –≤–∞–ґ–љ–µ–є—И–Є—Е –њ–Њ–ї–Њ–ґ–µ–љ–Є—П–є –њ–µ—А–≤–Њ–є —А–∞–±–Њ—В—Л –®—А–µ–і–Є–љ–≥–µ—А–∞
–њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ. –®—А–µ–і–Є–љ–≥–µ—А, –њ–Њ–і–Њ–±–љ–Њ –Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і—Г, –љ–∞—З–Є–љ–∞–µ—В —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞—В—М
—Б–≤–Њ–є —А–µ—Ж–µ–њ—В –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П —Б —Е–Њ—А–Њ—И–Њ –Є–Ј–≤–µ—Б—В–љ–Њ–≥–Њ –≤ –љ–∞—З–∞–ї–µ XX –≤–µ–Ї–∞ –ї—О–±–Њ–Љ—Г —Д–Є–Ј–Є–Ї—Г
—Б –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є—П –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є –і–ї—П –Ї–Њ–љ—Б–µ—А–≤–∞—В–Є–≤–љ–Њ–є
—Б–Є—Б—В–µ–Љ—Л:
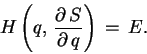 |
(2) |
–Я–Њ–і 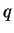 –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–љ–Є–Љ–∞–µ—В —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М –≤—Б–µ—Е –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —Б–Є—Б—В–µ–Љ—Л,
–®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–љ–Є–Љ–∞–µ—В —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М –≤—Б–µ—Е –Њ–±–Њ–±—Й–µ–љ–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —Б–Є—Б—В–µ–Љ—Л, 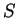 -–і–µ–є—Б—В–≤–Є–µ –Є–ї–Є —Г–Ї–Њ—А–Њ—З–µ–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ, —З—В–Њ
–і–ї—П —Б–ї—Г—З–∞—П –Ї–Њ–љ—Б–µ—А–≤–∞—В–Є–≤–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –љ–µ –Є–≥—А–∞–µ—В –±–Њ–ї—М—И–Њ–є —А–Њ–ї–Є, —З–∞—Б—В–љ–∞—П
–њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –і–µ–є—Б—В–≤–Є—П –њ–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–µ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є –Њ–±–Њ–±—Й–µ–љ–љ—Л–є
–Є–Љ–њ—Г–ї—М—Б, –∞
-–і–µ–є—Б—В–≤–Є–µ –Є–ї–Є —Г–Ї–Њ—А–Њ—З–µ–љ–љ–Њ–µ –і–µ–є—Б—В–≤–Є–µ, —З—В–Њ
–і–ї—П —Б–ї—Г—З–∞—П –Ї–Њ–љ—Б–µ—А–≤–∞—В–Є–≤–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –љ–µ –Є–≥—А–∞–µ—В –±–Њ–ї—М—И–Њ–є —А–Њ–ї–Є, —З–∞—Б—В–љ–∞—П
–њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –і–µ–є—Б—В–≤–Є—П –њ–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–µ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є –Њ–±–Њ–±—Й–µ–љ–љ—Л–є
–Є–Љ–њ—Г–ї—М—Б, –∞ 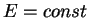 - —Н–љ–µ—А–≥–Є—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Г—А–Њ–≤–љ—П. –ѓ—Б–љ–Њ—Б—В—М –Є –њ—А–Њ–Ј—А–∞—З–љ–Њ—Б—В—М
–Є—Б—Е–Њ–і–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞, –Ї–Њ—В–Њ—А—Л–є –њ–Њ–ї–Њ–ґ–µ–љ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –≤ –Њ—Б–љ–Њ–≤—Г —Б–≤–Њ–µ–є —В–µ–Њ—А–Є–Є,
—Б —Б–∞–Љ–Њ–≥–Њ –љ–∞—З–∞–ї–∞ –і–µ–ї–∞–µ—В –µ–µ –±–Њ–ї–µ–µ –њ—А–µ–і–њ–Њ–і—З—В–Є—В–µ–ї—М–љ–Њ–є –і–ї—П –≤–Њ—Б–њ—А–Є—П—В–Є—П —И–Є—А–Њ–Ї–Є–Љ–Є
–Ї—А—Г–≥–∞–Љ–Є —Д–Є–Ј–Є–Ї–Њ–≤, –љ–µ–ґ–µ–ї–Є –±–µ–Ј—Г—Б–ї–Њ–≤–љ–∞—П –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ—Б—В—М, –љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–∞—П —Б–ї–Њ–ґ–љ–Њ—Б—В—М
–Є—Б—Е–Њ–і–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞.
- —Н–љ–µ—А–≥–Є—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Г—А–Њ–≤–љ—П. –ѓ—Б–љ–Њ—Б—В—М –Є –њ—А–Њ–Ј—А–∞—З–љ–Њ—Б—В—М
–Є—Б—Е–Њ–і–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞, –Ї–Њ—В–Њ—А—Л–є –њ–Њ–ї–Њ–ґ–µ–љ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –≤ –Њ—Б–љ–Њ–≤—Г —Б–≤–Њ–µ–є —В–µ–Њ—А–Є–Є,
—Б —Б–∞–Љ–Њ–≥–Њ –љ–∞—З–∞–ї–∞ –і–µ–ї–∞–µ—В –µ–µ –±–Њ–ї–µ–µ –њ—А–µ–і–њ–Њ–і—З—В–Є—В–µ–ї—М–љ–Њ–є –і–ї—П –≤–Њ—Б–њ—А–Є—П—В–Є—П —И–Є—А–Њ–Ї–Є–Љ–Є
–Ї—А—Г–≥–∞–Љ–Є —Д–Є–Ј–Є–Ї–Њ–≤, –љ–µ–ґ–µ–ї–Є –±–µ–Ј—Г—Б–ї–Њ–≤–љ–∞—П –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ—Б—В—М, –љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–∞—П —Б–ї–Њ–ґ–љ–Њ—Б—В—М
–Є—Б—Е–Њ–і–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞ –Љ–∞—В—А–Є—З–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –У–µ–є–Ј–µ–љ–±–µ—А–≥–∞.
–Ш—Й–µ—В—Б—П —А–µ—И–µ–љ–Є–µ 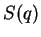 –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (2),
"–њ—А–µ–і—Б—В–∞–≤–ї—П—О—Й–µ–µ —Б–Њ–±–Њ–є —Б—Г–Љ–Љ—Г —Д—Г–љ–Ї—Ж–Є–є, –Ї–∞–ґ–і–∞—П –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –Ј–∞–≤–Є—Б–Є—В —В–Њ–ї—М–Ї–Њ
–Њ—В –Њ–і–љ–Њ–є –Є–Ј –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (2),
"–њ—А–µ–і—Б—В–∞–≤–ї—П—О—Й–µ–µ —Б–Њ–±–Њ–є —Б—Г–Љ–Љ—Г —Д—Г–љ–Ї—Ж–Є–є, –Ї–∞–ґ–і–∞—П –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –Ј–∞–≤–Є—Б–Є—В —В–Њ–ї—М–Ї–Њ
–Њ—В –Њ–і–љ–Њ–є –Є–Ј –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е 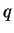 ". –Ъ–∞–ґ–і—Л–є, –Ї—В–Њ –Є–Ј—Г—З–∞–ї –Ї—Г—А—Б
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є, –±–µ–Ј —В—А—Г–і–∞ –њ–Њ–є–Љ–µ—В, —З—В–Њ –і–ї—П —А–µ—И–µ–љ–Є—П —Б–≤–Њ–µ–≥–Њ
—Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П —Б—В–∞–љ–і–∞—А—В–љ–Њ–є –њ—А–Њ—Ж–µ–і—Г—А–Њ–є —А–∞–Ј–і–µ–ї–µ–љ–Є—П
–њ–µ—А–µ–Љ–µ–љ–љ—Л—Е, –Ї–Њ—В–Њ—А–∞—П —И–Є—А–Њ–Ї–Њ –њ—А–Є–Љ–µ–љ—П–ї–∞—Б—М –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є XX –≤–µ–Ї–∞. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ
–≤—А–µ–Љ—П –Љ–µ—В–Њ–і —А–∞–Ј–і–µ–ї–µ–љ–Є—П –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —В–∞–Ї–ґ–µ —П–≤–ї—П–µ—В—Б—П –Њ—Б–љ–Њ–≤–љ—Л–Љ –њ–Њ–і—Е–Њ–і–Њ–Љ –њ—А–Є —А–µ—И–µ–љ–Є–Є
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –°–ї–µ–і—Г—О—Й–Є–Љ —И–∞–≥–Њ–Љ –®—А–µ–і–Є–љ–≥–µ—А –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В –Ј–∞–Љ–µ–љ—Г
–њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –≤ (2). –Ю–љ –≤–≤–Њ–і–Є—В –љ–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О
". –Ъ–∞–ґ–і—Л–є, –Ї—В–Њ –Є–Ј—Г—З–∞–ї –Ї—Г—А—Б
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є, –±–µ–Ј —В—А—Г–і–∞ –њ–Њ–є–Љ–µ—В, —З—В–Њ –і–ї—П —А–µ—И–µ–љ–Є—П —Б–≤–Њ–µ–≥–Њ
—Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П —Б—В–∞–љ–і–∞—А—В–љ–Њ–є –њ—А–Њ—Ж–µ–і—Г—А–Њ–є —А–∞–Ј–і–µ–ї–µ–љ–Є—П
–њ–µ—А–µ–Љ–µ–љ–љ—Л—Е, –Ї–Њ—В–Њ—А–∞—П —И–Є—А–Њ–Ї–Њ –њ—А–Є–Љ–µ–љ—П–ї–∞—Б—М –≤ –њ–µ—А–≤–Њ–є —З–µ—В–≤–µ—А—В–Є XX –≤–µ–Ї–∞. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ
–≤—А–µ–Љ—П –Љ–µ—В–Њ–і —А–∞–Ј–і–µ–ї–µ–љ–Є—П –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —В–∞–Ї–ґ–µ —П–≤–ї—П–µ—В—Б—П –Њ—Б–љ–Њ–≤–љ—Л–Љ –њ–Њ–і—Е–Њ–і–Њ–Љ –њ—А–Є —А–µ—И–µ–љ–Є–Є
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –°–ї–µ–і—Г—О—Й–Є–Љ —И–∞–≥–Њ–Љ –®—А–µ–і–Є–љ–≥–µ—А –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В –Ј–∞–Љ–µ–љ—Г
–њ–µ—А–µ–Љ–µ–љ–љ—Л—Е –≤ (2). –Ю–љ –≤–≤–Њ–і–Є—В –љ–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О 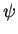 —Б–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—О:
—Б–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—О:
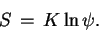 |
(3) |
–Ш–Ј —Б–≤–Њ–є—Б—В–≤ –ї–Њ–≥–∞—А–Є—Д–Љ–Њ–≤ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —Д—Г–љ–Ї—Ж–Є—П 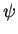 –Є–Љ–µ–µ—В "–≤–Є–і –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П
—Д—Г–љ–Ї—Ж–Є–є, –Ј–∞–≤–Є—Б—П—Й–Є—Е —В–Њ–ї—М–Ї–Њ –Њ—В –Њ–і–љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л". –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤–њ–µ—А–≤—Л–µ
–≤ —Д–Є–Ј–Є–Ї—Г –±—Л–ї–∞ –≤–≤–µ–і–µ–љ–∞ –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, —Е–Њ—В—П –≤
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —А–∞–±–Њ—В–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ —Н—В–Њ—В —В–µ—А–Љ–Є–љ –µ—Й–µ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В. –Я–Њ —Б–Љ—Л—Б–ї—Г
–њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П (3), —Д—Г–љ–Ї—Ж–Є—П
–Є–Љ–µ–µ—В "–≤–Є–і –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П
—Д—Г–љ–Ї—Ж–Є–є, –Ј–∞–≤–Є—Б—П—Й–Є—Е —В–Њ–ї—М–Ї–Њ –Њ—В –Њ–і–љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л". –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤–њ–µ—А–≤—Л–µ
–≤ —Д–Є–Ј–Є–Ї—Г –±—Л–ї–∞ –≤–≤–µ–і–µ–љ–∞ –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, —Е–Њ—В—П –≤
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —А–∞–±–Њ—В–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ —Н—В–Њ—В —В–µ—А–Љ–Є–љ –µ—Й–µ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В. –Я–Њ —Б–Љ—Л—Б–ї—Г
–њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П (3), —Д—Г–љ–Ї—Ж–Є—П 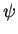 –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–є,
–Њ–і–љ–∞–Ї–Њ —Б–њ–µ—Ж–Є–∞–ї—М–љ–Њ —Н—В–Њ —Г—Б–ї–Њ–≤–Є–µ –≤ —Б—В–∞—В—М–µ –љ–µ –Њ–≥–Њ–≤–∞—А–Є–≤–∞–µ—В—Б—П.
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–Њ–Ј–ґ–µ —Д–Є–Ј–Є–Ї–Є –њ–Њ–є–Љ—Г—В, —З—В–Њ –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–ґ–µ—В
–±—Л—В—М –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–∞, –∞ –њ–Њ—В–Њ–Љ—Г –Ј–∞–Љ–µ–љ–∞ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е (3) –љ–µ–Ї–Њ—А—А–µ–Ї—В–љ–∞.
–і–Њ–ї–ґ–љ–∞ –±—Л—В—М –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–є,
–Њ–і–љ–∞–Ї–Њ —Б–њ–µ—Ж–Є–∞–ї—М–љ–Њ —Н—В–Њ —Г—Б–ї–Њ–≤–Є–µ –≤ —Б—В–∞—В—М–µ –љ–µ –Њ–≥–Њ–≤–∞—А–Є–≤–∞–µ—В—Б—П.
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–Њ–Ј–ґ–µ —Д–Є–Ј–Є–Ї–Є –њ–Њ–є–Љ—Г—В, —З—В–Њ –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –Љ–Њ–ґ–µ—В
–±—Л—В—М –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–∞, –∞ –њ–Њ—В–Њ–Љ—Г –Ј–∞–Љ–µ–љ–∞ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е (3) –љ–µ–Ї–Њ—А—А–µ–Ї—В–љ–∞.
–Т–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, —Б –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ—Б—В—М—О –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –®—А–µ–і–Є–љ–≥–µ—А –і–Њ–ї–ґ–µ–љ –±—Л–ї
—Б—В–Њ–ї–Ї–љ—Г—В—М—Б—П —Г–ґ–µ –≤ —Б–≤–Њ–µ–є –њ–µ—А–≤–Њ–є —А–∞–±–Њ—В–µ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П
(8) –і–ї—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞ –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е 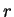 ,
, 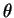 ,
,
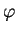 –Є–Љ–µ–µ—В —Б–ї–µ–і—Г—О—Й–Є–є –≤–Є–і ([10] —Б—В—А.206):
–Є–Љ–µ–µ—В —Б–ї–µ–і—Г—О—Й–Є–є –≤–Є–і ([10] —Б—В—А.206):
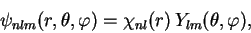
–≥–і–µ 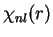 -—А–∞–і–Є–∞–ї—М–љ–∞—П –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П,
-—А–∞–і–Є–∞–ї—М–љ–∞—П –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П,
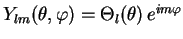 -—И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П,
–≤ –Ї–Њ—В–Њ—А–Њ–є —Б–Њ—Б—А–µ–і–Њ—В–Њ—З–µ–љ–∞ –≤—Б—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В —Г–≥–ї–Њ–≤,
-—И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П,
–≤ –Ї–Њ—В–Њ—А–Њ–є —Б–Њ—Б—А–µ–і–Њ—В–Њ—З–µ–љ–∞ –≤—Б—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –Њ—В —Г–≥–ї–Њ–≤, 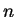 -–≥–ї–∞–≤–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ
—З–Є—Б–ї–Њ,
-–≥–ї–∞–≤–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ
—З–Є—Б–ї–Њ, 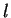 -–Њ—А–±–Є—В–∞–ї—М–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ (–љ–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ –µ—Б–ї–Є –≥–ї–∞–≤–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ
—З–Є—Б–ї–Њ –Ј–∞–і–∞–љ–Њ, —В–Њ –Њ—А–±–Є—В–∞–ї—М–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В –њ—А–Є–љ–Є–Љ–∞—В—М –Ј–љ–∞—З–µ–љ–Є—П
-–Њ—А–±–Є—В–∞–ї—М–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ (–љ–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ –µ—Б–ї–Є –≥–ї–∞–≤–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ
—З–Є—Б–ї–Њ –Ј–∞–і–∞–љ–Њ, —В–Њ –Њ—А–±–Є—В–∞–ї—М–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В –њ—А–Є–љ–Є–Љ–∞—В—М –Ј–љ–∞—З–µ–љ–Є—П
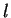 =0, 1, 2, ...
=0, 1, 2, ... 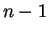 ),
), 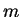 -–Љ–∞–≥–љ–Є—В–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ (–Ї–Њ—В–Њ—А–Њ–µ –њ—А–Є –Ј–∞–і–∞–љ–љ–Њ–Љ
-–Љ–∞–≥–љ–Є—В–љ–Њ–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–µ —З–Є—Б–ї–Њ (–Ї–Њ—В–Њ—А–Њ–µ –њ—А–Є –Ј–∞–і–∞–љ–љ–Њ–Љ
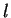 —А–∞–≤–љ–Њ
—А–∞–≤–љ–Њ
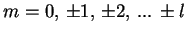 ). –Я–Њ—Н—В–Њ–Љ—Г, –≤ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞
). –Я–Њ—Н—В–Њ–Љ—Г, –≤ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞
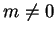 –Є
–Є 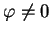 , —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, –∞ –≤–Љ–µ—Б—В–µ —Б –љ–µ–є –Є –≤–Њ–ї–љ–Њ–≤–∞—П
—Д—Г–љ–Ї—Ж–Є—П
, —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, –∞ –≤–Љ–µ—Б—В–µ —Б –љ–µ–є –Є –≤–Њ–ї–љ–Њ–≤–∞—П
—Д—Г–љ–Ї—Ж–Є—П 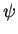 —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞, –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л.
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Б–Њ—Б—В–Њ—П–љ–Є—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞, –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л.
–Ю–і–љ–∞–Ї–Њ, –≤ –Њ–±—Б—Г–ґ–і–∞–µ–Љ–Њ–є —Б—В–∞—В—М–µ –®—А–µ–і–Є–љ–≥–µ—А —Е–Њ—В—П –Є —Г–њ–Њ–Љ–Є–љ–∞–µ—В –і–≤–∞–ґ–і—Л –Њ —И–∞—А–Њ–≤—Л—Е
—Д—Г–љ–Ї—Ж–Є—П—Е (–≤ –њ–µ—А–≤—Л–є —А–∞–Ј –Њ–љ–Є –µ–Љ—Г –љ—Г–ґ–љ—Л, —З—В–Њ–±—Л –њ–Њ–Ї–∞–Ј–∞—В—М —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В—М
–Њ—А–±–Є—В–∞–ї—М–љ–Њ–≥–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —З–Є—Б–ї–∞ 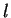 ), –љ–Њ –љ–Є–≥–і–µ —П–≤–љ–Њ –Є—Е –љ–µ –≤—Л–њ–Є—Б—Л–≤–∞–µ—В, –∞ –Њ
–Љ–∞–≥–љ–Є—В–љ–Њ–Љ –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ —З–Є—Б–ї–µ –љ–µ —Г–њ–Њ–Љ–Є–љ–∞–µ—В –≤–Њ–≤—Б–µ. –Ґ–∞–Ї–Њ–є –њ–Њ–і—Е–Њ–і –≤—Л–Ј—Л–≤–∞–µ—В
–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–µ —Г–і–Є–≤–ї–µ–љ–Є–µ. –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –њ–Њ –≤—Б–µ–є –≤–Є–і–Є–Љ–Њ—Б—В–Є, —Б–∞–Љ –®—А–µ–і–Є–љ–≥–µ—А –≤–њ–µ—А–≤—Л–µ
—Б—В–Њ–ї–Ї–љ—Г–ї—Б—П —Б –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ—Б—В—М—О –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ –≤ —Б–ї–µ–і—Г—О—Й–Є—Е
—Б–≤–Њ–Є—Е —А–∞–±–Њ—В–∞—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї —А–∞–Ј–≤–Є—В–Є–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л –≤–Њ –≤—А–µ–Љ–µ–љ–Є. –Э–Њ, –і–∞–ґ–µ,
–љ–µ —Б–Љ–Њ—В—А—П –љ–∞ —Н—В–Њ, –µ—Й–µ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –і–Њ–ї–≥–Њ–µ –≤—А–µ–Љ—П —Г—В–≤–µ—А–ґ–і–∞–ї: "–Э–µ–њ—А–Є—П—В–љ–Њ - –њ—А–Њ—В–Є–≤
—Н—В–Њ–≥–Њ –і–∞–ґ–µ —Б–ї–µ–і—Г–µ—В –≤–Њ–Ј—А–∞–ґ–∞—В—М - –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е —З–Є—Б–µ–ї.
), –љ–Њ –љ–Є–≥–і–µ —П–≤–љ–Њ –Є—Е –љ–µ –≤—Л–њ–Є—Б—Л–≤–∞–µ—В, –∞ –Њ
–Љ–∞–≥–љ–Є—В–љ–Њ–Љ –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ —З–Є—Б–ї–µ –љ–µ —Г–њ–Њ–Љ–Є–љ–∞–µ—В –≤–Њ–≤—Б–µ. –Ґ–∞–Ї–Њ–є –њ–Њ–і—Е–Њ–і –≤—Л–Ј—Л–≤–∞–µ—В
–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–µ —Г–і–Є–≤–ї–µ–љ–Є–µ. –С–Њ–ї–µ–µ —В–Њ–≥–Њ, –њ–Њ –≤—Б–µ–є –≤–Є–і–Є–Љ–Њ—Б—В–Є, —Б–∞–Љ –®—А–µ–і–Є–љ–≥–µ—А –≤–њ–µ—А–≤—Л–µ
—Б—В–Њ–ї–Ї–љ—Г–ї—Б—П —Б –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ—Б—В—М—О –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ –≤ —Б–ї–µ–і—Г—О—Й–Є—Е
—Б–≤–Њ–Є—Е —А–∞–±–Њ—В–∞—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї —А–∞–Ј–≤–Є—В–Є–µ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л –≤–Њ –≤—А–µ–Љ–µ–љ–Є. –Э–Њ, –і–∞–ґ–µ,
–љ–µ —Б–Љ–Њ—В—А—П –љ–∞ —Н—В–Њ, –µ—Й–µ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –і–Њ–ї–≥–Њ–µ –≤—А–µ–Љ—П —Г—В–≤–µ—А–ґ–і–∞–ї: "–Э–µ–њ—А–Є—П—В–љ–Њ - –њ—А–Њ—В–Є–≤
—Н—В–Њ–≥–Њ –і–∞–ґ–µ —Б–ї–µ–і—Г–µ—В –≤–Њ–Ј—А–∞–ґ–∞—В—М - –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е —З–Є—Б–µ–ї. 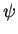 –≤—Б–µ-—В–∞–Ї–Є —А–µ–∞–ї—М–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П..." (—Б–Љ. [5], —Б—В—А.204).
–≤—Б–µ-—В–∞–Ї–Є —А–µ–∞–ї—М–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П..." (—Б–Љ. [5], —Б—В—А.204).
–Я—А–Њ—Б–ї–µ–і–Є–Љ –і–∞–ї–µ–µ –Ј–∞ —Е–Њ–і–Њ–Љ –Љ—Л—Б–ї–µ–є –Є —Д–Њ—А–Љ–Њ–є –Є–Ј–ї–Њ–ґ–µ–љ–Є—П –≠.–®—А–µ–і–Є–љ–≥–µ—А–∞. "–Я–Њ—Б—В–Њ—П–љ–љ—Г—О
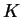 –њ—А–Є—Е–Њ–і–Є—В—Б—П –≤–≤–µ—Б—В–Є –Є–Ј —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є, —Б–Њ–≥–ї–∞—Б–љ–Њ –Ї–Њ—В–Њ—А—Л–Љ –Њ–љ–∞
–і–Њ–ї–ґ–љ–∞ –Њ–±–ї–∞–і–∞—В—М —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М—О –і–µ–є—Б—В–≤–Є—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–∞–µ–Љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ
–њ—А–Є—Е–Њ–і–Є—В—Б—П –≤–≤–µ—Б—В–Є –Є–Ј —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є, —Б–Њ–≥–ї–∞—Б–љ–Њ –Ї–Њ—В–Њ—А—Л–Љ –Њ–љ–∞
–і–Њ–ї–ґ–љ–∞ –Њ–±–ї–∞–і–∞—В—М —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М—О –і–µ–є—Б—В–≤–Є—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–∞–µ–Љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ
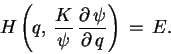 |
(4) |
... –Я—А–Є –њ—А–µ–љ–µ–±—А–µ–ґ–µ–љ–Є–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П–Љ–Є –Љ–∞—Б—Б—Л —Г—А–∞–≤–љ–µ–љ–Є–µ (4) –Љ–Њ–ґ–љ–Њ –≤—Б–µ–≥–і–∞
—Б–≤–µ—Б—В–Є, –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –≤ —Б–ї—Г—З–∞–µ –Њ–і–љ–Њ—Н–ї–µ–Ї—В—А–Њ–љ–љ–Њ–є –њ—А–Њ–±–ї–µ–Љ—Л, –Ї —Б–ї—Г–і—Г—О—Й–µ–Љ—Г
–≤–Є–і—Г: –Ї–≤–∞–і—А–∞—В–Є—З–љ–∞—П —Д–Њ—А–Љ–∞ –Њ—В —Д—Г–љ–Ї—Ж–Є–Є 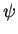 –Є –µ–µ –њ–µ—А–≤—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е —А–∞–≤–љ–∞
–љ—Г–ї—О." –Ф–ї—П —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤ –∞—В–Њ–Љ–µ –≤–Њ–і–Њ—А–Њ–і–∞ –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –і–∞–љ–љ–∞—П
–Ї–≤–∞–і—А–∞—В–Є—З–љ–∞—П —Д–Њ—А–Љ–∞ –Є–Љ–µ–µ—В –≤–Є–і:
–Є –µ–µ –њ–µ—А–≤—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е —А–∞–≤–љ–∞
–љ—Г–ї—О." –Ф–ї—П —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤ –∞—В–Њ–Љ–µ –≤–Њ–і–Њ—А–Њ–і–∞ –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –і–∞–љ–љ–∞—П
–Ї–≤–∞–і—А–∞—В–Є—З–љ–∞—П —Д–Њ—А–Љ–∞ –Є–Љ–µ–µ—В –≤–Є–і:
–≥–і–µ
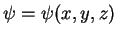 ,
,
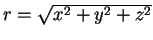 ,
, 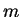 -–Љ–∞—Б—Б–∞ —Н–ї–µ–Ї—В—А–Њ–љ–∞,
-–Љ–∞—Б—Б–∞ —Н–ї–µ–Ї—В—А–Њ–љ–∞,
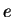 -–µ–≥–Њ –Ј–∞—А—П–і. –Я–Њ—Б–ї–µ –Њ—З–µ–≤–Є–і–љ—Л—Е –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М (—Г—З–Є—В—Л–≤–∞–µ–Љ, —З—В–Њ
-–µ–≥–Њ –Ј–∞—А—П–і. –Я–Њ—Б–ї–µ –Њ—З–µ–≤–Є–і–љ—Л—Е –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М (—Г—З–Є—В—Л–≤–∞–µ–Љ, —З—В–Њ
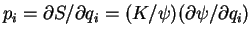 ):
):
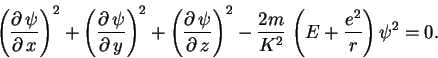 |
(5) |
–°–ї–µ–і—Г—О—Й–∞—П —Д—А–∞–Ј–∞ —П–≤–ї—П–µ—В—Б—П –Ї–ї—О—З–µ–≤–Њ–є –і–ї—П –≤—Б–µ–є –њ–µ—А–≤–Њ–є —А–∞–±–Њ—В—Л –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є
–Љ–µ—Е–∞–љ–Є–Ї–µ. "–Ш—Й–µ–Љ —В–∞–Ї—Г—О –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ—Г—О (–ї–Є—И–љ–µ–µ –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–Є–µ —В–Њ–≥–Њ, —З—В–Њ
–≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –љ–µ —Б—З–Є—В–∞–µ—В—Б—П –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–є - –Э.–Э.) –≤–Њ –≤—Б–µ–Љ –Ї–Њ–љ—Д–Є–≥—Г—А–∞—Ж–Є–Њ–љ–љ–Њ–Љ
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Њ–і–љ–Њ–Ј–љ–∞—З–љ—Г—О –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Г—О –Є –≤—Б—О–і—Г –і–≤–∞–ґ–і—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ—Г—О
—Д—Г–љ–Ї—Ж–Є—О 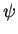 , –Ї–Њ—В–Њ—А–∞—П –і–∞–µ—В —Н–Ї—Б—В—А–µ–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–љ—В–µ–≥—А–∞–ї—Г –Њ—В —Г–њ–Њ–Љ—П–љ—Г—В–Њ–є
–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д–Њ—А–Љ—Л (—В–Њ –µ—Б—В—М —Д–Њ—А–Љ—Л (5)-–Э.–Э.), —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–љ–Њ–Љ—Г
–њ–Њ –≤—Б–µ–Љ—Г –Ї—А–љ—Д–Є–≥—Г—А–∞—Ж–Є–Њ–љ–љ–Њ–Љ—Г –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤—Г. –≠—В–∞ –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞
–Є –Ј–∞–Љ–µ–љ—П–µ—В —Г –љ–∞—Б –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—Б–ї–Њ–≤–Є—П." –£–Ї–∞–Ј–∞–љ–љ–∞—П –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞ –і–ї—П
–∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞ –Є–Љ–µ–µ—В –≤–Є–і:
, –Ї–Њ—В–Њ—А–∞—П –і–∞–µ—В —Н–Ї—Б—В—А–µ–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–љ—В–µ–≥—А–∞–ї—Г –Њ—В —Г–њ–Њ–Љ—П–љ—Г—В–Њ–є
–Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д–Њ—А–Љ—Л (—В–Њ –µ—Б—В—М —Д–Њ—А–Љ—Л (5)-–Э.–Э.), —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–љ–Њ–Љ—Г
–њ–Њ –≤—Б–µ–Љ—Г –Ї—А–љ—Д–Є–≥—Г—А–∞—Ж–Є–Њ–љ–љ–Њ–Љ—Г –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤—Г. –≠—В–∞ –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞
–Є –Ј–∞–Љ–µ–љ—П–µ—В —Г –љ–∞—Б –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—Б–ї–Њ–≤–Є—П." –£–Ї–∞–Ј–∞–љ–љ–∞—П –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞ –і–ї—П
–∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞ –Є–Љ–µ–µ—В –≤–Є–і:
![\begin{displaymath}
\delta J =\delta\,\int\int\int\, dx\, dy\, dz\,
\left [
\lef...
...rac{2m}{K^2}\,\left (E+\frac{e^2}{r}\right )\psi^2
\right ]=0.
\end{displaymath}](img37.gif) |
(6) |
"–Ш–љ—В–µ–≥—А–∞–ї –±–µ—А–µ—В—Б—П –Ј–і–µ—Б—М –њ–Њ –≤—Б–µ–Љ—Г –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤—Г. –Ю–±—Л—З–љ—Л–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ –Њ—В—Б—О–і–∞
–њ–Њ–ї—Г—З–∞–µ–Љ
![\begin{displaymath}
\frac{1}{2}\,\delta J\,
=\,\int\, df\,\delta\psi\,\frac{\par...
...ac{2m}{K^2}\,\left (E+\frac{e^2}{r}\right )\,\psi
\right ] =0.
\end{displaymath}](img38.gif) |
(7) |
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–Њ–ї–ґ–љ–Њ –±—Л—В—М, –≤–Њ-–њ–µ—А–≤—Л—Е, —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ
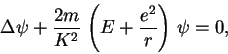 |
(8) |
–Є, –≤–Њ-–≤—В–Њ—А—Л—Е, –і–Њ–ї–ґ–µ–љ —А–∞–≤–љ—П—В—М—Б—П –љ—Г–ї—О —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–љ—Л–є –њ–Њ –≤—Б–µ–є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ
—Г–і–∞–ї–µ–љ–љ–Њ–є –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є–љ—В–µ–≥—А–∞–ї"
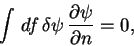 |
(9) |
–≥–і–µ 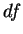 -—Н–ї–µ–Љ–µ–љ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ —Г–і–∞–ї–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞
-—Н–ї–µ–Љ–µ–љ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ —Г–і–∞–ї–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ 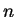 -–љ–Њ—А–Љ–∞–ї—М –Ї
–њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є.
-–љ–Њ—А–Љ–∞–ї—М –Ї
–њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є.
–Т–Њ—В –Є –≤—Б–µ. –Я–Њ–ї—Г—З–Є–≤—И–µ–µ—Б—П —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ (8) —В–µ–њ–µ—А—М –љ–∞–Ј—Л–≤–∞—О—В
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞ –≤ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–Љ
–њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–Є. –Ю–љ–Њ –і–Њ–њ—Г—Б–Ї–∞–µ—В –Њ—З–µ–≤–Є–і–љ–Њ–µ –Њ–±–Њ—Й–µ–љ–Є–µ –љ–∞ –ї—О–±–Њ–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ
–њ–Њ–ї–µ –Є —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Њ–є –Є–Ј –і–≤—Г—Е –≤–µ—А—И–Є–љ —А–∞–±–Њ—В—Л –≠—А–≤–Є–љ–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Ї–∞–Ї
—Д–Є–Ј–Є–Ї–∞-—В–µ–Њ—А–µ—В–Є–Ї–∞. –Ч–∞ –љ–Є–Љ –њ–Њ—Б–ї–µ–і—Г—О—В —В–µ–Њ—А–Є—П –≤–Њ–Ј–Љ—Г—Й–µ–љ–Є–є –Є –љ–µ—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ
—Г—А–∞–≤–љ–µ–љ–Є–µ (–≤—В–Њ—А–∞—П –≤–µ—А—И–Є–љ–∞), –Љ–љ–Њ–≥–Њ—З–Є—Б–ї–µ–љ–љ—Л–µ –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П –Ї –Ї–Њ–љ–Ї—А–µ—В–љ—Л–Љ –њ—А–Њ–±–ї–µ–Љ–∞–Љ
–Љ–Є–Ї—А–Њ–Љ–Є—А–∞, –Њ–±–Њ–±—Й–µ–љ–Є—П –і–ї—П —З–∞—Б—В–Є—Ж —Б–Њ —Б–њ–Є–љ–Њ–Љ –Є —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є—Е —З–∞—Б—В–Є—Ж, –љ–Њ
–Є–Љ–µ–љ–љ–Њ –њ—А–Є –њ–Њ–Љ–Њ—Й–Є —Г—А–∞–≤–љ–µ–љ–Є—П (8) –±—Л–ї —Б–Њ–≤–µ—А—И–µ–љ —А–µ—И–∞—О—Й–Є–є –њ—А–Њ—А—Л–≤ –≤
–њ–Њ–љ–Є–Љ–∞–љ–Є–Є –Ј–∞–Ї–Њ–љ–Њ–≤ –Љ–Є–Ї—А–Њ–Љ–Є—А–∞.
–Ю—Б—В–∞–ї–Њ—Б—М –µ—Й–µ –Љ–љ–Њ–≥–Њ –≤–Њ–њ—А–Њ—Б–Њ–≤, –љ–∞ –Ї–Њ—В–Њ—А—Л–µ —Е–Њ—В–µ–ї–Њ—Б—М –±—Л –њ–Њ–ї—Г—З–Є—В—М –Њ—В–≤–µ—В—Л.
–Т–Њ-–њ–µ—А–≤—Л—Е, —З—В–Њ –і–µ–ї–∞—В—М —Б —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ (5), –≤–µ–і—М —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ
–Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є–є (5) –Є (8) —А–∞–Ј–ї–Є—З–љ—Л?
–Т–Њ-–≤—В–Њ—А—Л—Е, –Ј–∞—З–µ–Љ –њ–Њ–љ–∞–і–Њ–±–Є–ї–Њ—Б—М –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –љ–∞ –њ—Г—Б—В–Њ–Љ –Љ–µ—Б—В–µ –≤–≤–Њ–і–Є—В—М
–≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ (6), –Ї–Њ—В–Њ—А—Л–є –њ–Њ –Ј–∞–≥–∞–і–Њ—З–љ–Њ—Б—В–Є —Б–≤–Њ–µ–≥–Њ
–њ—А–Њ–Є—Б—Е–Њ–ґ–і–µ–љ–Є—П –Љ–Њ–ґ–µ—В –њ–Њ—Б–њ–Њ—А–Є—В—М —Б –њ—А–∞–≤–Є–ї–Њ–Љ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞?
–§–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤—Л—Е–Њ–і–Є—В —В–∞–Ї, —З—В–Њ –љ–µ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –њ—А—П–Љ–Њ–≥–Њ –ї–Њ–≥–Є—З–µ—Б–Ї–Њ–≥–Њ
–њ–µ—А–µ—Е–Њ–і–∞ –Њ—В —Г—А–∞–≤–љ–µ–љ–Є–є –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є (4) –Ї –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–Љ—Г
–њ—А–Є–љ—Ж–Є–њ—Г (6). –Ш, –љ–∞–Ї–Њ–љ–µ—Ж, –Ї–∞–Ї–Њ–≤ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –≤–≤–µ–і–µ–љ–љ–Њ–є
–≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ –Ј–∞–Љ–µ–љ—Л –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е (3) –Ј–∞–≥–∞–і–Њ—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є 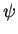 ?
–Э–Є –љ–∞ –Њ–і–Є–љ –Є–Ј —Н—В–Є—Е –≤–Њ–њ—А–Њ—Б–Њ–≤, –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, –Є—Б–Ї–ї—О—З–∞—П –њ–Њ—Б–ї–µ–і–љ–µ–≥–Њ, –њ–µ—А–≤–∞—П
—Б—В–∞—В—М—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –љ–µ –і–∞–µ—В —З–µ—В–Ї–Њ–≥–Њ –Њ—В–≤–µ—В–∞. –Я–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј–љ–Є–Ї–∞–µ—В
–њ–Њ–і–Њ–Ј—А–µ–љ–Є–µ, —З—В–Њ –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–ї—Г—З–Є–ї —Г—А–∞–≤–љ–µ–љ–Є–µ (8)
–Є–љ—Л–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ, –∞ –њ–Њ—В–Њ–Љ, —Г–ґ–µ –Ј–љ–∞—П –њ—А–∞–≤–Є–ї—М–љ—Л–є –Њ—В–≤–µ—В, –њ–Њ–њ—Л—В–∞–ї—Б—П
–≤—Л–≤–µ—Б—В–Є –µ–≥–Њ –±–Њ–ї–µ–µ –љ–∞—Г–Ї–Њ–Њ–±—А–∞–Ј–љ–Њ –Љ–µ—В–Њ–і–∞–Љ–Є, –љ–∞–Є–±–Њ–ї–µ–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–љ—Л–Љ–Є
–≤ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–µ –љ–∞—З–∞–ї–∞ XX –≤–µ–Ї–∞. –Т –њ–Њ–ї—М–Ј—Г –њ–Њ–і–Њ–±–љ–Њ–≥–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П
—Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤—Г–µ—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Д–∞–Ї—В–Њ–≤.
?
–Э–Є –љ–∞ –Њ–і–Є–љ –Є–Ј —Н—В–Є—Е –≤–Њ–њ—А–Њ—Б–Њ–≤, –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, –Є—Б–Ї–ї—О—З–∞—П –њ–Њ—Б–ї–µ–і–љ–µ–≥–Њ, –њ–µ—А–≤–∞—П
—Б—В–∞—В—М—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –љ–µ –і–∞–µ—В —З–µ—В–Ї–Њ–≥–Њ –Њ—В–≤–µ—В–∞. –Я–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј–љ–Є–Ї–∞–µ—В
–њ–Њ–і–Њ–Ј—А–µ–љ–Є–µ, —З—В–Њ –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ –®—А–µ–і–Є–љ–≥–µ—А –њ–Њ–ї—Г—З–Є–ї —Г—А–∞–≤–љ–µ–љ–Є–µ (8)
–Є–љ—Л–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ, –∞ –њ–Њ—В–Њ–Љ, —Г–ґ–µ –Ј–љ–∞—П –њ—А–∞–≤–Є–ї—М–љ—Л–є –Њ—В–≤–µ—В, –њ–Њ–њ—Л—В–∞–ї—Б—П
–≤—Л–≤–µ—Б—В–Є –µ–≥–Њ –±–Њ–ї–µ–µ –љ–∞—Г–Ї–Њ–Њ–±—А–∞–Ј–љ–Њ –Љ–µ—В–Њ–і–∞–Љ–Є, –љ–∞–Є–±–Њ–ї–µ–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–љ—Л–Љ–Є
–≤ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–µ –љ–∞—З–∞–ї–∞ XX –≤–µ–Ї–∞. –Т –њ–Њ–ї—М–Ј—Г –њ–Њ–і–Њ–±–љ–Њ–≥–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П
—Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤—Г–µ—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Д–∞–Ї—В–Њ–≤.
–§–∞–Ї—В –њ–µ—А–≤—Л–є. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –љ–µ–Њ–ґ–Є–і–∞–љ–љ–Њ, –њ–Њ –Ї—А–∞–є–љ–µ–є –Љ–µ—А–µ –Є–Ј –ї–Њ–≥–Є–Ї–Є —Б—В–∞—В—М–Є
—Н—В–Њ –љ–µ —Б–ї–µ–і—Г–µ—В, –њ—А–Є –њ–Њ–њ—Л—В–Ї–µ –Њ–±–Њ–Ј–љ–∞—З–Є—В—М —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–µ
—Б–Њ–і–µ—А–ґ–∞–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є 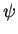 , –®—А–µ–і–Є–љ–≥–µ—А –њ–Є—И–µ—В: "–Ф–Њ–≤–Њ–ї—М–љ–Њ –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ
—Б–≤—П–Ј—Л–≤–∞—В—М —Д—Г–љ–Ї—Ж–Є—О
, –®—А–µ–і–Є–љ–≥–µ—А –њ–Є—И–µ—В: "–Ф–Њ–≤–Њ–ї—М–љ–Њ –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ
—Б–≤—П–Ј—Л–≤–∞—В—М —Д—Г–љ–Ї—Ж–Є—О 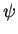 —Б –љ–µ–Ї–Њ—В–Њ—А—Л–Љ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ—Л–Љ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ –≤ –∞—В–Њ–Љ–µ,
–≤ –Ї–Њ—В–Њ—А–Њ–Љ —А–µ–∞–ї—М–љ–Њ—Б—В—М —Н–ї–µ–Ї—В—А–Њ–љ–љ—Л—Е —В—А–∞–µ–Ї—В–Њ—А–Є–є –≤ –њ–Њ—Б–ї–µ–і–љ–µ–µ –≤—А–µ–Љ—П
–љ–µ–Њ–і–љ–Њ–Ї—А–∞—В–љ–Њ –њ–Њ–і–≤–µ—А–≥–∞–ї–∞—Б—М —Б–Њ–Љ–љ–µ–љ–Є—О (—З—В–Њ —Н—В–Њ, –љ–∞–Љ–µ–Ї –љ–∞ —Б—В–∞—В—М—О [1]
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞?)" –Є —З—В–Њ "–њ—А–Є –њ–µ—А–µ—Е–Њ–і–µ —Н–љ–µ—А–≥–Є–Є –Њ—В –Њ–і–љ–Њ–≥–Њ —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П
–Ї –і—А—Г–≥–Њ–Љ—Г –њ–Њ—П–≤–ї—П–µ—В—Б—П –љ–µ—З—В–Њ (–њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ, —Б–≤–µ—В–Њ–≤–∞—П –≤–Њ–ї–љ–∞ - –Э.–Э.) —Б
—З–∞—Б—В–Њ—В–Њ–є, —А–∞–≤–љ–Њ–є —А–∞–Ј–љ–Њ—Б—В–Є —З–∞—Б—В–Њ—В —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є". –Ф–∞–ї–µ–µ,
"—Б–≤–µ—В–Њ–≤–∞—П –≤–Њ–ї–љ–∞ –њ—А–Є—З–Є–љ–љ–Њ —Б–≤—П–Ј–∞–љ–∞ —Б –±–Є–µ–љ–Є—П–Љ–Є, –њ–Њ—П–≤–ї—П—О—Й–Є–Љ–Є—Б—П –≤—Б–µ–≥–і–∞ –њ—А–Є
–њ–Њ–і–Њ–±–љ—Л—Е –њ–µ—А–µ—Е–Њ–і–∞—Е –≤ –ї—О–±–Њ–є —В–Њ—З–Ї–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞", –∞ "—З–∞—Б—В–Њ—В–∞ —Б–≤–µ—В–∞
–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —З–Є—Б–ї–Њ–Љ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–Њ–≤, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А—Л–µ –њ—А–Њ—Е–Њ–і–Є—В –љ–∞—И –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ—Л–є
–њ—А–Њ—Ж–µ—Б—Б –Ј–∞ —Б–µ–Ї—Г–љ–і—Г". –Я—А–Є —Н—В–Њ–Љ –®—А–µ–і–Є–љ–≥–µ—А –Њ—Б–Њ–±–Њ –њ–Њ–і—З–µ—А–Ї–Є–≤–∞–µ—В, —З—В–Њ –Њ–љ
—Б–љ–∞—З–∞–ї–∞ "—Е–Њ—В–µ–ї –Њ–±–Њ—Б–љ–Њ–≤–∞—В—М –љ–Њ–≤–Њ–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ –Ї–≤–∞–љ—В–Њ–≤—Л—Е –њ—А–∞–≤–Є–ї,
–Є—Б–њ–Њ–ї—М–Ј—Г—П —Г–Ї–∞–Ј–∞–љ–љ—Л–є —Б—А–∞–≤–љ–Є—В–µ–ї—М–љ–Њ –љ–∞–≥–ї—П–і–љ—Л–є –њ—Г—В—М, –љ–Њ
–њ–Њ—В–Њ–Љ –њ—А–µ–і–њ–Њ—З–µ–ї —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ—Л–є –≤ —Б—В–∞—В—М–µ —З–Є—Б—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є —Б–њ–Њ—Б–Њ–±,
—В–∞–Ї –Ї–∞–Ї –Њ–љ –і–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –ї—Г—З—И–µ –≤—Л—П—Б–љ–Є—В—М –≤—Б–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л
–≤–Њ–њ—А–Њ—Б–∞." –І—В–Њ –ґ–µ, –≤ —В–∞–Ї–Њ–Љ —Б–ї—Г—З–∞–µ, –®—А–µ–і–Є–љ–≥–µ—А—Г –Ї–∞–ґ–µ—В—Б—П –±–Њ–ї–µ–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ,
—З–µ–Љ –љ–∞–≥–ї—П–і–љ—Л–є –≤—Л–≤–Њ–і —Г—А–∞–≤–љ–µ–љ–Є—П (8)? –Р –≤–Њ—В —З—В–Њ: "–°—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ
–Љ–љ–µ –Ї–∞–ґ–µ—В—Б—П —В–Њ, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤—Л–µ –њ—А–∞–≤–Є–ї–∞ –љ–µ –≤–≤–Њ–і—П—В—Б—П –±–Њ–ї—М—И–µ –Ї–∞–Ї –Ј–∞–≥–∞–і–Њ—З–љ–Њ–µ
"—В—А–µ–±–Њ–≤–∞–љ–Є–µ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є" (—Б–Љ. —Г—А–∞–≤–љ–µ–љ–Є–µ (1) - –Э.–Э.)
–∞ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М—О –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ—Б—В–Є –Є –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ—Б—В–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–є
–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є". –Ґ–Њ –µ—Б—В—М —Б–∞–Љ—Л–Љ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ
–®—А–µ–і–Є–љ–≥–µ—А—Г –Ї–∞–ґ–µ—В—Б—П —В–Њ, —З—В–Њ –Њ–љ —Б–Љ–Њ–≥ –Њ–њ–Є—Б–∞—В—М —В–∞–Є–љ—Б—В–≤–µ–љ–љ—Л–µ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —П–≤–ї–µ–љ–Є—П
–Љ–µ—В–Њ–і–∞–Љ–Є, —Е–∞—А–∞–Ї—В–µ—А–љ—Л–Љ–Є –і–ї—П —Б—Г–≥—Г–±–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є.
–Ю—Б–љ–Њ–≤—Л–≤–∞—П—Б—М –љ–∞ —Б–≤–Њ–µ–Љ –њ–Њ–љ–Є–Љ–∞–љ–Є–Є —Д–Є–Ј–Є–Ї–Є –≤–љ—Г—В—А–Є–∞—В–Њ–Љ–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤, –®—А–µ–і–Є–љ–≥–µ—А
—Б–Љ–µ–ї–Њ –≤—Б—В—Г–њ–∞–µ—В –≤ –њ–Њ–ї–µ–Љ–Є–Ї—Г —Б –С–Њ—А–Њ–Љ: "–Э–µ —В—А–µ–±—Г–µ—В –Њ—Б–Њ–±—Л—Е —А–∞–Ј—К—П—Б–љ–µ–љ–Є–є —В–Њ
–Њ–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤–Њ, —З—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –њ—А–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ –њ–µ—А–µ—Е–Њ–і–µ
—Н–љ–µ—А–≥–Є—П –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –Є–Ј –Њ–і–љ–Њ–є –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–є —Д–Њ—А–Љ—Л –≤ –і—А—Г–≥—Г—О –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ
–±–Њ–ї–µ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В–µ–ї—М–љ–Њ, —З–µ–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –Њ –њ–µ—А–µ—Б–Ї–∞–Ї–Є–≤–∞—О—Й–µ–Љ —Н–ї–µ–Ї—В—А–Њ–љ–µ.
–Ш–Ј–Љ–µ–љ–µ–љ–Є–µ —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–µ—В –њ—А–Њ–Є—Б—Е–Њ–і–Є—В—М –љ–µ–њ—А–µ—А—Л–≤–љ–Њ –≤
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Є –≤—А–µ–Љ–µ–љ–Є, –Њ–љ–Њ –Љ–Њ–ґ–µ—В –і–ї–Є—В—М—Б—П –≤—А–µ–Љ—П, —А–∞–≤–љ–Њ–µ –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–Њ–Љ—Г
—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ –≤—А–µ–Љ–µ–љ–Є –њ—А–Њ—Ж–µ—Б—Б–∞ –Є–Ј–ї—Г—З–µ–љ–Є—П...".
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–µ—А–ґ–∞—Б—М –њ—А–Є–≤—Л—З–љ–Њ–≥–Њ –±–µ—А–µ–≥–∞, –≥—А–µ—З–µ—Б–Ї–Є–µ –Љ–Њ—А–µ—Е–Њ–і—Л –њ—А–Є–њ–ї—Л–ї–Є –≤
–љ–Њ–≤—Л–µ –Ј–µ–Љ–ї–Є, –±–Њ–ї–µ–µ —В–Њ–≥–Њ, –љ–∞ –Є–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤—Л–є –Љ–∞—В–µ—А–Є–Ї, —Е–Њ—В—П —Б–∞–Љ–Є –Њ–љ–Є –љ–∞–Є–≤–љ–Њ
–њ–Њ–ї–∞–≥–∞—О—В, —З—В–Њ –љ–∞—Е–Њ–і—П—В—Б—П —Б–Њ–≤—Б–µ–Љ –љ–µ–і–∞–ї–µ–Ї–Њ –Њ—В —А–Њ–і–љ–Њ–≥–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–≥–Њ –і–Њ–Љ–∞!
—Б –љ–µ–Ї–Њ—В–Њ—А—Л–Љ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ—Л–Љ –њ—А–Њ—Ж–µ—Б—Б–Њ–Љ –≤ –∞—В–Њ–Љ–µ,
–≤ –Ї–Њ—В–Њ—А–Њ–Љ —А–µ–∞–ї—М–љ–Њ—Б—В—М —Н–ї–µ–Ї—В—А–Њ–љ–љ—Л—Е —В—А–∞–µ–Ї—В–Њ—А–Є–є –≤ –њ–Њ—Б–ї–µ–і–љ–µ–µ –≤—А–µ–Љ—П
–љ–µ–Њ–і–љ–Њ–Ї—А–∞—В–љ–Њ –њ–Њ–і–≤–µ—А–≥–∞–ї–∞—Б—М —Б–Њ–Љ–љ–µ–љ–Є—О (—З—В–Њ —Н—В–Њ, –љ–∞–Љ–µ–Ї –љ–∞ —Б—В–∞—В—М—О [1]
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞?)" –Є —З—В–Њ "–њ—А–Є –њ–µ—А–µ—Е–Њ–і–µ —Н–љ–µ—А–≥–Є–Є –Њ—В –Њ–і–љ–Њ–≥–Њ —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П
–Ї –і—А—Г–≥–Њ–Љ—Г –њ–Њ—П–≤–ї—П–µ—В—Б—П –љ–µ—З—В–Њ (–њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ, —Б–≤–µ—В–Њ–≤–∞—П –≤–Њ–ї–љ–∞ - –Э.–Э.) —Б
—З–∞—Б—В–Њ—В–Њ–є, —А–∞–≤–љ–Њ–є —А–∞–Ј–љ–Њ—Б—В–Є —З–∞—Б—В–Њ—В —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є". –Ф–∞–ї–µ–µ,
"—Б–≤–µ—В–Њ–≤–∞—П –≤–Њ–ї–љ–∞ –њ—А–Є—З–Є–љ–љ–Њ —Б–≤—П–Ј–∞–љ–∞ —Б –±–Є–µ–љ–Є—П–Љ–Є, –њ–Њ—П–≤–ї—П—О—Й–Є–Љ–Є—Б—П –≤—Б–µ–≥–і–∞ –њ—А–Є
–њ–Њ–і–Њ–±–љ—Л—Е –њ–µ—А–µ—Е–Њ–і–∞—Е –≤ –ї—О–±–Њ–є —В–Њ—З–Ї–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞", –∞ "—З–∞—Б—В–Њ—В–∞ —Б–≤–µ—В–∞
–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —З–Є—Б–ї–Њ–Љ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–Њ–≤, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А—Л–µ –њ—А–Њ—Е–Њ–і–Є—В –љ–∞—И –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ—Л–є
–њ—А–Њ—Ж–µ—Б—Б –Ј–∞ —Б–µ–Ї—Г–љ–і—Г". –Я—А–Є —Н—В–Њ–Љ –®—А–µ–і–Є–љ–≥–µ—А –Њ—Б–Њ–±–Њ –њ–Њ–і—З–µ—А–Ї–Є–≤–∞–µ—В, —З—В–Њ –Њ–љ
—Б–љ–∞—З–∞–ї–∞ "—Е–Њ—В–µ–ї –Њ–±–Њ—Б–љ–Њ–≤–∞—В—М –љ–Њ–≤–Њ–µ –њ–Њ–љ–Є–Љ–∞–љ–Є–µ –Ї–≤–∞–љ—В–Њ–≤—Л—Е –њ—А–∞–≤–Є–ї,
–Є—Б–њ–Њ–ї—М–Ј—Г—П —Г–Ї–∞–Ј–∞–љ–љ—Л–є —Б—А–∞–≤–љ–Є—В–µ–ї—М–љ–Њ –љ–∞–≥–ї—П–і–љ—Л–є –њ—Г—В—М, –љ–Њ
–њ–Њ—В–Њ–Љ –њ—А–µ–і–њ–Њ—З–µ–ї —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ—Л–є –≤ —Б—В–∞—В—М–µ —З–Є—Б—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є —Б–њ–Њ—Б–Њ–±,
—В–∞–Ї –Ї–∞–Ї –Њ–љ –і–∞–µ—В –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –ї—Г—З—И–µ –≤—Л—П—Б–љ–Є—В—М –≤—Б–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–µ —Б—В–Њ—А–Њ–љ—Л
–≤–Њ–њ—А–Њ—Б–∞." –І—В–Њ –ґ–µ, –≤ —В–∞–Ї–Њ–Љ —Б–ї—Г—З–∞–µ, –®—А–µ–і–Є–љ–≥–µ—А—Г –Ї–∞–ґ–µ—В—Б—П –±–Њ–ї–µ–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ,
—З–µ–Љ –љ–∞–≥–ї—П–і–љ—Л–є –≤—Л–≤–Њ–і —Г—А–∞–≤–љ–µ–љ–Є—П (8)? –Р –≤–Њ—В —З—В–Њ: "–°—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ
–Љ–љ–µ –Ї–∞–ґ–µ—В—Б—П —В–Њ, —З—В–Њ –Ї–≤–∞–љ—В–Њ–≤—Л–µ –њ—А–∞–≤–Є–ї–∞ –љ–µ –≤–≤–Њ–і—П—В—Б—П –±–Њ–ї—М—И–µ –Ї–∞–Ї –Ј–∞–≥–∞–і–Њ—З–љ–Њ–µ
"—В—А–µ–±–Њ–≤–∞–љ–Є–µ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є" (—Б–Љ. —Г—А–∞–≤–љ–µ–љ–Є–µ (1) - –Э.–Э.)
–∞ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М—О –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ—Б—В–Є –Є –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ—Б—В–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–є
–Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є". –Ґ–Њ –µ—Б—В—М —Б–∞–Љ—Л–Љ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ
–®—А–µ–і–Є–љ–≥–µ—А—Г –Ї–∞–ґ–µ—В—Б—П —В–Њ, —З—В–Њ –Њ–љ —Б–Љ–Њ–≥ –Њ–њ–Є—Б–∞—В—М —В–∞–Є–љ—Б—В–≤–µ–љ–љ—Л–µ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —П–≤–ї–µ–љ–Є—П
–Љ–µ—В–Њ–і–∞–Љ–Є, —Е–∞—А–∞–Ї—В–µ—А–љ—Л–Љ–Є –і–ї—П —Б—Г–≥—Г–±–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є.
–Ю—Б–љ–Њ–≤—Л–≤–∞—П—Б—М –љ–∞ —Б–≤–Њ–µ–Љ –њ–Њ–љ–Є–Љ–∞–љ–Є–Є —Д–Є–Ј–Є–Ї–Є –≤–љ—Г—В—А–Є–∞—В–Њ–Љ–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤, –®—А–µ–і–Є–љ–≥–µ—А
—Б–Љ–µ–ї–Њ –≤—Б—В—Г–њ–∞–µ—В –≤ –њ–Њ–ї–µ–Љ–Є–Ї—Г —Б –С–Њ—А–Њ–Љ: "–Э–µ —В—А–µ–±—Г–µ—В –Њ—Б–Њ–±—Л—Е —А–∞–Ј—К—П—Б–љ–µ–љ–Є–є —В–Њ
–Њ–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤–Њ, —З—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –њ—А–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ –њ–µ—А–µ—Е–Њ–і–µ
—Н–љ–µ—А–≥–Є—П –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –Є–Ј –Њ–і–љ–Њ–є –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–є —Д–Њ—А–Љ—Л –≤ –і—А—Г–≥—Г—О –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ
–±–Њ–ї–µ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В–µ–ї—М–љ–Њ, —З–µ–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –Њ –њ–µ—А–µ—Б–Ї–∞–Ї–Є–≤–∞—О—Й–µ–Љ —Н–ї–µ–Ї—В—А–Њ–љ–µ.
–Ш–Ј–Љ–µ–љ–µ–љ–Є–µ —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–µ—В –њ—А–Њ–Є—Б—Е–Њ–і–Є—В—М –љ–µ–њ—А–µ—А—Л–≤–љ–Њ –≤
–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Є –≤—А–µ–Љ–µ–љ–Є, –Њ–љ–Њ –Љ–Њ–ґ–µ—В –і–ї–Є—В—М—Б—П –≤—А–µ–Љ—П, —А–∞–≤–љ–Њ–µ –Њ–њ—А–µ–і–µ–ї—П–µ–Љ–Њ–Љ—Г
—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ –≤—А–µ–Љ–µ–љ–Є –њ—А–Њ—Ж–µ—Б—Б–∞ –Є–Ј–ї—Г—З–µ–љ–Є—П...".
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–µ—А–ґ–∞—Б—М –њ—А–Є–≤—Л—З–љ–Њ–≥–Њ –±–µ—А–µ–≥–∞, –≥—А–µ—З–µ—Б–Ї–Є–µ –Љ–Њ—А–µ—Е–Њ–і—Л –њ—А–Є–њ–ї—Л–ї–Є –≤
–љ–Њ–≤—Л–µ –Ј–µ–Љ–ї–Є, –±–Њ–ї–µ–µ —В–Њ–≥–Њ, –љ–∞ –Є–љ–Њ–є –Ї–≤–∞–љ—В–Њ–≤—Л–є –Љ–∞—В–µ—А–Є–Ї, —Е–Њ—В—П —Б–∞–Љ–Є –Њ–љ–Є –љ–∞–Є–≤–љ–Њ
–њ–Њ–ї–∞–≥–∞—О—В, —З—В–Њ –љ–∞—Е–Њ–і—П—В—Б—П —Б–Њ–≤—Б–µ–Љ –љ–µ–і–∞–ї–µ–Ї–Њ –Њ—В —А–Њ–і–љ–Њ–≥–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–≥–Њ –і–Њ–Љ–∞!
–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –®—А–µ–і–Є–љ–≥–µ—А –Њ—И–Є–±–∞–ї—Б—П, –Ї–Њ–≥–і–∞ –њ–Њ–ї–∞–≥–∞–ї –Ј–∞–Ї—А—Л—В—Л–Љ
—А–∞–Ј –Є –љ–∞–≤—Б–µ–≥–і–∞ –≤–Њ–њ—А–Њ—Б –Њ –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–Ї–∞—З–Ї–∞—Е. –Я–Њ–њ—Л—В–Ї–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ–≥–Њ
–Њ–њ–Є—Б–∞–љ–Є—П –Є–Ј–ї—Г—З–µ–љ–Є—П –∞—В–Њ–Љ–∞ –Ї–∞–Ї –њ—А–Њ—Ж–µ—Б—Б–∞ –±–Є–µ–љ–Є—П, –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–≥–Њ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ
–Є –≤—А–µ–Љ–µ–љ–Є, –љ–µ —Г–і–∞–ї–∞—Б—М, –Ї–∞–Ї –Ј–∞ —З–µ—В–≤–µ—А—В—М –≤–µ–Ї–∞ –і–Њ —В–Њ–≥–Њ –њ–Њ–і–Њ–±–љ–∞—П –њ–Њ–њ—Л—В–Ї–∞ –љ–µ
—Г–і–∞–ї–∞—Б—М –Ь–∞–Ї—Б—Г –Я–ї–∞–љ–Ї—Г –≤ –≤–Њ–њ—А–Њ—Б–µ –Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ –Њ–њ–Є—Б–∞–љ–Є–Є –Є–Ј–ї—Г—З–µ–љ–Є—П –∞–±—Б–Њ–ї—О—В–љ–Њ
—З–µ—А–љ–Њ–≥–Њ —В–µ–ї–∞. –Ч–∞–≥–∞–і–Њ—З–љ—Л–µ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Б–Ї–∞—З–Ї–Є –±–ї–∞–≥–Њ–њ–Њ–ї—Г—З–љ–Њ —Б—Г—Й–µ—Б—В–≤—Г—О—В –≤ —Д–Є–Ј–Є–Ї–µ
–і–Њ –љ–∞—Б—В–Њ—П—Й–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є. –І–∞—Й–µ –≤—Б–µ–≥–Њ –Њ –љ–Є—Е –≤—Б–њ–Њ–Љ–Є–љ–∞—О—В –≤—Б–≤—П–Ј–Є —Б –њ—А–Њ–±–ї–µ–Љ–Њ–є
—А–µ–і—Г–Ї—Ж–Є–Є (—Б—В—П–≥–Є–≤–∞–љ–Є—П) –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤ –њ—А–Њ—Ж–µ—Б—Б–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л
–Љ–∞–Ї—А–Њ–њ—А–Є–±–Њ—А–Њ–Љ. –≠—В–∞ –њ—А–Њ–±–ї–µ–Љ–∞ –љ–µ –Є–Љ–µ–µ—В —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В–µ–ї—М–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –Є –њ–Њ —Б–µ–є
–і–µ–љ—М.
–§–∞–Ї—В –≤—В–Њ—А–Њ–є. –Я—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤–њ—А—П–Љ—Г—О –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Є –њ—Г—В—М, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г
–њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ –®—А–µ–і–Є–љ–≥–µ—А –њ—А–Є—И–µ–ї –Ї —Г—А–∞–≤–љ–µ–љ–Є—О (8) –Њ—В—В–∞–ї–Ї–Є–≤–∞—П—Б—М
–Њ—В "–±–µ–Ј—Г–Љ–љ–Њ–є" –≤ —В–Њ –≤—А–µ–Љ—П –µ—Й–µ —В–≤–µ—А–і–Њ –љ–µ –њ–Њ–і—В–≤–µ—А–ґ–і–µ–љ–љ–Њ–є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ
–≥–Є–њ–Њ—В–µ–Ј—Л –Ы. –і–µ –С—А–Њ–є–ї—П –Њ –≤–Њ–ї–љ–∞—Е –Љ–∞—В–µ—А–Є–Є (–≤—Б–њ–Њ–Љ–љ–Є—В–µ, —А–µ–Ј—Г–ї—М—В–∞—В—Л –Њ–њ—Л—В–Њ–≤
–Ф—Н–≤–Є—Б—Б–Њ–љ–∞ –Є –Ф–ґ–µ—А–Љ–µ—А–∞ –њ–Њ –љ–∞–±–ї—О–і–µ–љ–Є—О –і–Є—Д—А–∞–Ї—Ж–Є–Є —Н–ї–µ–Ї—В—А–Њ–љ–Њ–≤ –љ–∞ –Ї—А–Є—Б—В–∞–ї–ї–µ
—Б—В–∞–ї–Є –Є–Ј–≤–µ—Б—В–љ—Л —В–Њ–ї—М–Ї–Њ –≤ 1927 –≥–Њ–і—Г, —Е–Њ—В—П –њ–µ—А–≤—Л–µ —Б–≤–µ–і–µ–љ–Є—П –Њ –њ–Њ—Б—В–∞–љ–Њ–≤–Ї–µ
—Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞ –Њ—В–љ–Њ—Б—П—В—Б—П –Ї 1925 –≥–Њ–і—Г): "–Я—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ,
–љ–µ–ї—М–Ј—П –љ–µ —Г–њ–Њ–Љ—П–љ—Г—В—М, —З—В–Њ –Њ—Б–љ–Њ–≤–љ—Л–Љ –Є—Б—Е–Њ–і–љ—Л–Љ —В–Њ–ї—З–Ї–Њ–Љ, –Ї–Њ—В–Њ—А—Л–є –њ—А–Є–≤–µ–ї –Ї
–њ–Њ—П–≤–ї–µ–љ–Є—О –њ—А–Є–≤–µ–і–µ–љ–љ—Л—Е –Ј–і–µ—Б—М —А–∞—Б—Б—Г–ґ–і–µ–љ–Є–є, –±—Л–ї–∞ –і–Є—Б—Б–µ—А—В–∞—Ж–Є—П –і–µ –С—А–Њ–є–ї—П,
—Б–Њ–і–µ—А–ґ–∞—Й–∞—П –Љ–љ–Њ–≥–Њ –≥–ї—Г–±–Њ–Ї–Є—Е –Є–і–µ–є, –∞ —В–∞–Ї–ґ–µ —А–∞–Ј–Љ—Л—И–ї–µ–љ–Є–є –Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ–Њ–Љ
—А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–Є "—Д–∞–Ј–Њ–≤—Л—Е –≤–Њ–ї–љ"... –У–ї–∞–≤–љ–Њ–µ –Њ—В–ї–Є—З–Є–µ –Њ—В —В–µ–Њ—А–Є–Є –і–µ –С—А–Њ–є–ї—П,
–≤ –Ї–Њ—В–Њ—А–Њ–є –≥–Њ–≤–Њ—А–Є—В—Б—П –Њ –њ—А—П–Љ–Њ–ї–Є–љ–µ–є–љ–Њ —А–∞—Б–њ—А–Њ—Б—В—А–Њ–љ—П—О—Й–µ–є—Б—П –≤–Њ–ї–љ–µ, –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П
–Ј–і–µ—Б—М –≤ —В–Њ–Љ, —З—В–Њ –Љ—Л —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ, –µ—Б–ї–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –≤–Њ–ї–љ–Њ–≤—Г—О —В—А–∞–Ї—В–Њ–≤–Ї—Г,
—Б—В–Њ—П—З–Є–µ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ –Ї–Њ–ї–µ–±–∞–љ–Є—П (–≤ —В–Њ –≤—А–µ–Љ—П, –Ї–∞–Ї —Г –і–µ –С—А–Њ–є–ї—П
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—О—В—Б—П –±–µ–≥—Г—Й–Є–µ –≤–Њ–ї–љ—Л –Љ–∞—В–µ—А–Є–Є –≤ –≤–∞–Ї—Г—Г–Љ–µ - –Э.–Э.)." –Ч–∞–Љ–µ—З–∞—В–µ–ї—М–љ–Њ,
–љ–Њ —В–Њ–≥–і–∞ –њ—А–Є —З–µ–Љ —В—Г—В —Г—А–∞–≤–љ–µ–љ–Є—П –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є –Є –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ?
–Ш—Б—З–µ—А–њ—Л–≤–∞—О—Й–Є–є –Њ—В–≤–µ—В –і–∞–µ—В—Б—П –≤–Њ –≤—В–Њ—А–Њ–є —Б—В–∞—В—М–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Є–Ј —Ж–Є–Ї–ї–∞ "–Ъ–≤–∞–љ—В–Њ–≤–∞–љ–Є–µ
–Ї–∞–Ї –Ј–∞–і–∞—З–∞ –Њ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е", –Ї–Њ—В–Њ—А—Г—О –Љ—Л –љ–∞–і–µ–µ–Љ—Б—П –і–µ—В–∞–ї—М–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М
–≤ —Б–ї–µ–і—Г—О—Й–µ–є –Ј–∞–Љ–µ—В–Ї–µ. –Т –љ–µ–є —Г—А–∞–≤–љ–µ–љ–Є–µ (8) –њ–Њ–ї—Г—З–∞–µ—В—Б—П –∞–±—Б–Њ–ї—О—В–љ–Њ
–і—А—Г–≥–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ –њ—А–Є –њ–Њ–Љ–Њ—Й–Є –њ—А–Є–Љ–µ–љ–µ–љ–Є—П –Ї –љ–µ—А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї–Є–Љ –≤–Њ–ї–љ–∞–Љ –Љ–∞—В–µ—А–Є–Є
–Ы. –і–µ –С—А–Њ–є–ї—П –Њ–њ—В–Є–Ї–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є –∞–љ–∞–ї–Њ–≥–Є–Є –У–∞–Љ–Є–ї—М—В–Њ–љ–∞. –°–њ–Њ—Б–Њ–± –ї–µ–≥–Ї–Є–є,
–Ї—А–∞—Б–Є–≤—Л–є, –Њ—З–µ–љ—М –ї–Њ–≥–Є—З–љ—Л–є, –љ–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –љ–µ —Б—В—А–Њ–≥–Є–є –≤ –њ—А–Њ—В–Є–≤–Њ–≤–µ—Б
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Ї–Њ—А—А–µ–Ї—В–љ–Њ–≥–Њ, –љ–Њ "–љ–µ —П—Б–љ–Њ–≥–Њ —Б–∞–Љ–Њ–≥–Њ –њ–Њ —Б–µ–±–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
(3) –Є —Б—В–Њ–ї—М –ґ–µ –љ–µ —П—Б–љ–Њ–≥–Њ –њ–µ—А–µ—Е–Њ–і–∞ –Њ—В –њ—А–Є—А–∞–≤–љ–Є–≤–∞–љ–Є—П –љ—Г–ї—О –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ
–≤—Л—А–∞–ґ–µ–љ–Є—П –Ї —В—А–µ–±–Њ–≤–∞–љ–Є—О —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л–є –Є–љ—В–µ–≥—А–∞–ї –Њ—В —Н—В–Њ–≥–Њ –ґ–µ
–≤—Л—А–∞–ґ–µ–љ–Є—П –±—Л–ї —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ (—Н—В–Њ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —Б–ї–Њ–≤–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Є–Ј –≤—В–Њ—А–Њ–є
—Б—В–∞—В—М–Є, –≤ –Ї–Њ—В–Њ—А–Њ–є –Њ–љ –Ї–Њ–Љ–Љ–µ–љ—В–Є—А—Г–µ—В –њ–µ—А–≤—Г—О! - –Э.–Э.)". –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Б–Њ—Е—А–∞–љ–Є–ї–Њ—Б—М
–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Є—Б—В–Њ—А–Є—З–µ—Б–Ї–Є—Е —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤, –≤ –Ї–Њ—В–Њ—А—Л—Е –Ї–Њ–ї–ї–µ–≥–Є –®—А–µ–і–Є–љ–≥–µ—А–∞
–љ–∞—Б—В–∞–Є–≤–∞—О—В, —З—В–Њ –≤—Б–µ –љ–∞—З–∞–ї–Њ—Б—М –Є–Љ–µ–љ–љ–Њ —Б –Њ–њ—В–Є–Ї–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–є
–∞–љ–∞–ї–Њ–≥–Є–Є –У–∞–Љ–Є–ї—М—В–Њ–љ–∞, –њ—А–Є–Љ–µ–љ–µ–љ–љ–Њ–є –і–ї—П –±–Њ–ї–µ–µ —П—Б–љ–Њ–≥–Њ –њ–Њ–љ–Є–Љ–∞–љ–Є—П
—Б—Г—Й–љ–Њ—Б—В–Є –Є–і–µ–Є –≤–Њ–ї–љ –Љ–∞—В–µ—А–Є–Є –Ы. –і–µ –С—А–Њ–є–ї—П [9].
–Я—А–Є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–Є —Д—Г–љ–Ї—Ж–Є–Є 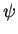 –Ї–∞–Ї –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ
—Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤ –∞—В–Њ–Љ–µ –®—А–µ–і–Є–љ–≥–µ—А
—Б—В–Њ–ї–Ї–љ—Г–ї—Б—П —Б –Њ–і–љ–Є–Љ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Б–µ—А—М–µ–Ј–љ—Л–Љ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–µ–Љ. –Ш–Ј —В–µ–Њ—А–Є–Є
–Ї–Њ–ї–µ–±–∞–љ–Є–є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –њ—А–Є –Ј–∞–і–∞–љ–Њ–є –∞–Љ–њ–ї–Є—В—Г–і–µ —Н–љ–µ—А–≥–Є—П
–Ї–Њ–ї–µ–±–∞–љ–Є–є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ –Ї–≤–∞–і—А–∞—В—Г —З–∞—Б—В–Њ—В—Л. –≠—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ —В–µ–Њ—А–Є–Є
–љ–Њ—Б–Є—В –Њ–±—Й–Є–є —Е–∞—А–∞–Ї—В–µ—А –Є –њ—А–Є–Љ–µ–љ–Є–Љ–Њ –Ї–Њ –≤—Б—П–Ї–Њ–Љ—Г –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–Љ—Г –њ—А–Њ—Ж–µ—Б—Б—Г.
–Х—Б–ї–Є –њ—А–Є–љ—П—В—М –µ–≥–Њ, —В–Њ —Н—В–Њ –њ—А–Є–≤–µ–ї–Њ –±—Л "–і–ї—П –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є
–Ї–∞–Ї –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ
—Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ —Н–ї–µ–Ї—В—А–Њ–љ–∞ –≤ –∞—В–Њ–Љ–µ –®—А–µ–і–Є–љ–≥–µ—А
—Б—В–Њ–ї–Ї–љ—Г–ї—Б—П —Б –Њ–і–љ–Є–Љ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Б–µ—А—М–µ–Ј–љ—Л–Љ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–µ–Љ. –Ш–Ј —В–µ–Њ—А–Є–Є
–Ї–Њ–ї–µ–±–∞–љ–Є–є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –њ—А–Є –Ј–∞–і–∞–љ–Њ–є –∞–Љ–њ–ї–Є—В—Г–і–µ —Н–љ–µ—А–≥–Є—П
–Ї–Њ–ї–µ–±–∞–љ–Є–є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ –Ї–≤–∞–і—А–∞—В—Г —З–∞—Б—В–Њ—В—Л. –≠—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ —В–µ–Њ—А–Є–Є
–љ–Њ—Б–Є—В –Њ–±—Й–Є–є —Е–∞—А–∞–Ї—В–µ—А –Є –њ—А–Є–Љ–µ–љ–Є–Љ–Њ –Ї–Њ –≤—Б—П–Ї–Њ–Љ—Г –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–Љ—Г –њ—А–Њ—Ж–µ—Б—Б—Г.
–Х—Б–ї–Є –њ—А–Є–љ—П—В—М –µ–≥–Њ, —В–Њ —Н—В–Њ –њ—А–Є–≤–µ–ї–Њ –±—Л "–і–ї—П –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є 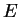 –Ї
–Љ–љ–Є–Љ—Л–Љ –Ј–љ–∞—З–µ–љ–Є—П–Љ —З–∞—Б—В–Њ—В—Л –Є, –Ї—А–Њ–Љ–µ —В–Њ–≥–Њ, –Є–љ—В—Г–Є—В–Є–≤–љ—Л–µ —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є—П
"–Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —В–µ–Њ—А–µ—В–Є–Ї–∞" (—В–Њ –µ—Б—В—М, –њ—А–∞–≤–Є–ї–Њ —З–∞—Б—В–Њ—В –С–Њ—А–∞, –Ї–Њ—В–Њ—А–Њ–µ –Њ–±—К—П—Б–љ—П–µ—В
—Д–µ–љ–Њ–Љ–µ–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–є –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ –†–Є—В—Ж–∞ - –Э.–Э.) –≥–Њ–≤–Њ—А—П—В,
—З—В–Њ –Ј–і–µ—Б—М –і–Њ–ї–ґ–љ–∞ –Є–Љ–µ—В—М –Љ–µ—Б—В–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В—М –Ј–љ–∞—З–µ–љ–Є—П
–Ї
–Љ–љ–Є–Љ—Л–Љ –Ј–љ–∞—З–µ–љ–Є—П–Љ —З–∞—Б—В–Њ—В—Л –Є, –Ї—А–Њ–Љ–µ —В–Њ–≥–Њ, –Є–љ—В—Г–Є—В–Є–≤–љ—Л–µ —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є—П
"–Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —В–µ–Њ—А–µ—В–Є–Ї–∞" (—В–Њ –µ—Б—В—М, –њ—А–∞–≤–Є–ї–Њ —З–∞—Б—В–Њ—В –С–Њ—А–∞, –Ї–Њ—В–Њ—А–Њ–µ –Њ–±—К—П—Б–љ—П–µ—В
—Д–µ–љ–Њ–Љ–µ–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–є –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ –†–Є—В—Ж–∞ - –Э.–Э.) –≥–Њ–≤–Њ—А—П—В,
—З—В–Њ –Ј–і–µ—Б—М –і–Њ–ї–ґ–љ–∞ –Є–Љ–µ—В—М –Љ–µ—Б—В–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В—М –Ј–љ–∞—З–µ–љ–Є—П 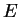 —Б–∞–Љ–Њ–є
—З–∞—Б—В–Њ—В–µ, –∞ –љ–µ –µ–µ –Ї–≤–∞–і—А–∞—В—Г".
—Б–∞–Љ–Њ–є
—З–∞—Б—В–Њ—В–µ, –∞ –љ–µ –µ–µ –Ї–≤–∞–і—А–∞—В—Г".
–Ъ–∞–Ї –ґ–µ –®—А–µ–і–Є–љ–≥–µ—А —Б–њ—А–∞–≤–ї—П–µ—В—Б—П —Б —Г–Ї–∞–Ј–∞–љ–љ—Л–Љ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–µ–Љ? "–Ф–ї—П –њ–∞—А–∞–Љ–µ—В—А–∞
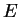 –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П (8) –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ–Њ –љ–µ —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ
–Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М". –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ —Н—В–Њ—В –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М
–Љ–љ–Њ–≥–Њ –±–Њ–ї—М—И–µ, —З–µ–Љ –ї—О–±–Њ–µ –Є–Ј –Є–Љ–µ—О—Й–Є—Е—Б—П –≤ –Ј–∞–і–∞—З–µ –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є
–≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П (8) –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ–Њ –љ–µ —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ
–Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М". –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ —Н—В–Њ—В –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М
–Љ–љ–Њ–≥–Њ –±–Њ–ї—М—И–µ, —З–µ–Љ –ї—О–±–Њ–µ –Є–Ј –Є–Љ–µ—О—Й–Є—Е—Б—П –≤ –Ј–∞–і–∞—З–µ –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є
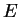 . –Э–∞–њ—А–Є–Љ–µ—А, –Љ–Њ–ґ–љ–Њ –≤—Б–њ–Њ–Љ–љ–Є—В—М —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї—Г—О —В–µ–Њ—А–Є—О –Є –њ—А–Є–љ—П—В—М –Ј–∞ –љ–∞—З–∞–ї–Њ
–Њ—В—Б—З–µ—В–∞ —Н–љ–µ—А–≥–Є—О –њ–Њ–Ї–Њ—П —Б–Є—Б—В–µ–Љ—Л. "–Ґ–Њ–≥–і–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ —З–∞—Б—В–Њ—В—Л –±—Г–і—Г—В
–і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ—Л –Є –Є—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Љ–∞–ї—Л–µ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ –Њ–Ї–∞–ґ—Г—В—Б—П
–њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л–Љ–Є
. –Э–∞–њ—А–Є–Љ–µ—А, –Љ–Њ–ґ–љ–Њ –≤—Б–њ–Њ–Љ–љ–Є—В—М —А–µ–ї—П—В–Є–≤–Є—Б—В—Б–Ї—Г—О —В–µ–Њ—А–Є—О –Є –њ—А–Є–љ—П—В—М –Ј–∞ –љ–∞—З–∞–ї–Њ
–Њ—В—Б—З–µ—В–∞ —Н–љ–µ—А–≥–Є—О –њ–Њ–Ї–Њ—П —Б–Є—Б—В–µ–Љ—Л. "–Ґ–Њ–≥–і–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ —З–∞—Б—В–Њ—В—Л –±—Г–і—Г—В
–і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ—Л –Є –Є—Е –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Љ–∞–ї—Л–µ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –љ–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ –Њ–Ї–∞–ґ—Г—В—Б—П
–њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л–Љ–Є 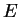 . –Э–Њ –Є–Љ–µ–љ–љ–Њ —Н—В–Њ–≥–Њ –Є —В—А–µ–±—Г–µ—В "–Є–љ—В—Г–Є—Ж–Є—П"
–Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —В–µ–Њ—А–µ—В–Є–Ї–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М —Н–љ–µ—А–≥–Є–Є –љ–µ —П–≤–ї—П–µ—В—Б—П
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ". –Ф–∞–љ–љ–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ
. –Э–Њ –Є–Љ–µ–љ–љ–Њ —Н—В–Њ–≥–Њ –Є —В—А–µ–±—Г–µ—В "–Є–љ—В—Г–Є—Ж–Є—П"
–Ї–≤–∞–љ—В–Њ–≤–Њ–≥–Њ —В–µ–Њ—А–µ—В–Є–Ї–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –љ—Г–ї–µ–≤–Њ–є —Г—А–Њ–≤–µ–љ—М —Н–љ–µ—А–≥–Є–Є –љ–µ —П–≤–ї—П–µ—В—Б—П
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ". –Ф–∞–љ–љ–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ
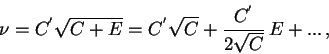 |
(10) |
–≥–і–µ 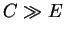 . –Т—Л—А–∞–ґ–µ–љ–Є–µ (10) –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ—А–Њ—П—Б–љ–Є—В—М –±–Њ—А–Њ–≤—Б–Ї–Њ–µ
—Г—Б–ї–Њ–≤–Є–µ –і–ї—П —З–∞—Б—В–Њ—В. "–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Н—В–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є—О —З–∞—Б—В–Њ—В–∞ –Є–Ј–ї—Г—З–µ–љ–Є—П
–њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ —А–∞–Ј–љ–Њ—Б—В–Є —Н–љ–µ—А–≥–Є–є, —В.–µ. —Б–Њ–≥–ї–∞—Б–љ–Њ (10) –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞
—А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ–Є —З–∞—Б—В–Њ—В–∞–Љ–Є
. –Т—Л—А–∞–ґ–µ–љ–Є–µ (10) –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ—А–Њ—П—Б–љ–Є—В—М –±–Њ—А–Њ–≤—Б–Ї–Њ–µ
—Г—Б–ї–Њ–≤–Є–µ –і–ї—П —З–∞—Б—В–Њ—В. "–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Н—В–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є—О —З–∞—Б—В–Њ—В–∞ –Є–Ј–ї—Г—З–µ–љ–Є—П
–њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞ —А–∞–Ј–љ–Њ—Б—В–Є —Н–љ–µ—А–≥–Є–є, —В.–µ. —Б–Њ–≥–ї–∞—Б–љ–Њ (10) –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–∞
—А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–Љ–Є —З–∞—Б—В–Њ—В–∞–Љ–Є 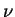 –≥–Є–њ–Њ—В–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ
–њ—А–Њ—Ж–µ—Б—Б–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Е–Њ—В—П –≤—Б–µ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —З–∞—Б—В–Њ—В—Л –Љ–љ–Њ–≥–Њ –±–Њ–ї—М—И–µ —З–∞—Б—В–Њ—В
–Є–Ј–ї—Г—З–µ–љ–Є—П, —Н—В–Є –і–≤–µ –≤–µ–ї–Є—З–Є–љ—Л —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ—Л –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ, –њ—А–Є—З–µ–Љ –њ–Њ—Б–ї–µ–і–љ—П—П
–Є–Ј –љ–Є—Е —П–≤–ї—П–µ—В—Б—П –Ї–∞–Ї –±—Л –≥–ї—Г–±–Њ–Ї–Є–Љ "—А–∞–Ј–љ–Њ—Б—В–љ—Л–Љ —В–Њ–љ–Њ–Љ" —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П,
–њ—А–Њ—В–µ–Ї–∞—О—Й–µ–≥–Њ —Б–Њ –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –±–Њ–ї—М—И–µ–є —З–∞—Б—В–Њ—В–Њ–є." –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г–Ї–∞–Ј–∞–љ–Њ–µ
–≤—Л—И–µ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–µ –њ–Њ–ї–љ–Њ—Б—В—М—О —Б–љ–Є–Љ–∞–µ—В—Б—П –≤–µ—Б—М–Љ–∞ –Є–Ј—П—Й–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ.
–≥–Є–њ–Њ—В–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ
–њ—А–Њ—Ж–µ—Б—Б–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Е–Њ—В—П –≤—Б–µ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —З–∞—Б—В–Њ—В—Л –Љ–љ–Њ–≥–Њ –±–Њ–ї—М—И–µ —З–∞—Б—В–Њ—В
–Є–Ј–ї—Г—З–µ–љ–Є—П, —Н—В–Є –і–≤–µ –≤–µ–ї–Є—З–Є–љ—Л —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ—Л –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ, –њ—А–Є—З–µ–Љ –њ–Њ—Б–ї–µ–і–љ—П—П
–Є–Ј –љ–Є—Е —П–≤–ї—П–µ—В—Б—П –Ї–∞–Ї –±—Л –≥–ї—Г–±–Њ–Ї–Є–Љ "—А–∞–Ј–љ–Њ—Б—В–љ—Л–Љ —В–Њ–љ–Њ–Љ" —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П,
–њ—А–Њ—В–µ–Ї–∞—О—Й–µ–≥–Њ —Б–Њ –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –±–Њ–ї—М—И–µ–є —З–∞—Б—В–Њ—В–Њ–є." –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г–Ї–∞–Ј–∞–љ–Њ–µ
–≤—Л—И–µ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є–µ –њ–Њ–ї–љ–Њ—Б—В—М—О —Б–љ–Є–Љ–∞–µ—В—Б—П –≤–µ—Б—М–Љ–∞ –Є–Ј—П—Й–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ.
–£–ґ–µ –≤ –њ–µ—А–≤–Њ–Љ —Б–Њ–Њ–±—Й–µ–љ–Є–Є –®—А–µ–і–Є–љ–≥–µ—А, –Њ–±–µ—Б–њ–Њ–Ї–Њ–Є–љ—Л–є –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–є —Н—Д–µ–Љ–µ—А–љ–Њ—Б—В—М—О
—Б–≤—П–Ј–Є –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ—А–Є–љ—Ж–Є–њ–∞ (6) —Б —Г—А–∞–≤–љ–µ–љ–Є—П–Љ–Є –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є
(4), –њ—А–µ–і–њ—А–Є–љ–Є–Љ–∞–µ—В –њ–Њ–њ—Л—В–Ї—Г –Є–љ–∞—З–µ —Б—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞—В—М
–≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ, –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–≥–Њ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М
—Г—А–∞–≤–љ–µ–љ–Є–µ (8). –° —Н—В–Њ–є —Ж–µ–ї—М—О –Њ–љ 28 —Д–µ–≤—А–∞–ї—П 1926 –≥–Њ–і–∞ –і–µ–ї–∞–µ—В
—Б–ї–µ–і—Г—О—Й–µ–µ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –њ—А–Є –Ї–Њ—А—А–µ–Ї—В—Г—А–µ. "–Т —Б–ї—Г—З–∞–µ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є
–Ї–Њ–љ—Б–µ—А–≤–∞—В–Є–≤–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Љ–Њ–ґ–љ–Њ —Б—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞—В—М –љ–∞—И—Г –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Г—О –Ј–∞–і–∞—З—Г –Є–Ј—П—Й–љ–µ–µ,
—З–µ–Љ —Н—В–Њ –±—Л–ї–Њ –Ј–і–µ—Б—М —Б–і–µ–ї–∞–љ–Њ, –±–µ–Ј –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ–є —Б–≤—П–Ј–Є —Б —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ
–У–∞–Љ–Є–ї—М—В–Њ–љ–∞ —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Я—Г—Б—В—М 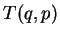 - –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П,
–Ј–∞–≤–Є—Б—П—Й–∞—П –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –Є–Љ–њ—Г–ї—М—Б–Њ–≤,
- –Ї–Є–љ–µ—В–Є—З–µ—Б–Ї–∞—П —Н–љ–µ—А–≥–Є—П,
–Ј–∞–≤–Є—Б—П—Й–∞—П –Њ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –Є–Љ–њ—Г–ї—М—Б–Њ–≤, 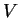 - –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П,
- –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Н–љ–µ—А–≥–Є—П,
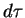 - "—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–љ—Л–є" –Њ–±—К–µ–Љ –Ї–Њ–љ—Д–Є–≥—Г—А–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞,
—В–Њ –µ—Б—В—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
- "—А–∞—Ж–Є–Њ–љ–∞–ї—М–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–љ—Л–є" –Њ–±—К–µ–Љ –Ї–Њ–љ—Д–Є–≥—Г—А–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞,
—В–Њ –µ—Б—В—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ
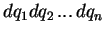 , —Г–Љ–љ–Њ–ґ–µ–љ–љ–Њ–µ –µ—Й–µ –љ–∞
–Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Є–Ј –і–Є—Б–Ї—А–Є–Љ–Є–љ–∞–љ—В–∞ –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д–Њ—А–Љ—Л
, —Г–Љ–љ–Њ–ґ–µ–љ–љ–Њ–µ –µ—Й–µ –љ–∞
–Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Є–Ј –і–Є—Б–Ї—А–Є–Љ–Є–љ–∞–љ—В–∞ –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ–є —Д–Њ—А–Љ—Л 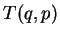 (—Б—А.: –У–Є–±–±—Б, "–°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞"). –Ґ–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
(—Б—А.: –У–Є–±–±—Б, "–°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞"). –Ґ–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є 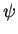 –і–Њ–ї–ґ–љ–Њ –њ—А–Є–і–∞–≤–∞—В—М "–Є–љ—В–µ–≥—А–∞–ї—Г –У–∞–Љ–Є–ї—М—В–Њ–љ–∞"
–і–Њ–ї–ґ–љ–Њ –њ—А–Є–і–∞–≤–∞—В—М "–Є–љ—В–µ–≥—А–∞–ї—Г –У–∞–Љ–Є–ї—М—В–Њ–љ–∞"
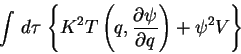 |
(11) |
—Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ—А–Є –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ–Љ –љ–Њ—А–Љ–Є—А—Г—О—Й–µ–Љ —Г—Б–ї–Њ–≤–Є–Є
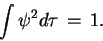 |
(12) |
C–Њ–±—Б—В–≤–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П —Н—В–Њ–є –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–є –њ—А–Њ–±–ї–µ–Љ—Л, —П–≤–ї—П—О—Й–Є–µ—Б—П, –Ї–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ,
—В–∞–Ї–ґ–µ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є –Є–љ—В–µ–≥—А–∞–ї–∞ (11), –і–∞—О—В —Б–Њ–≥–ї–∞—Б–љ–Њ –љ–∞—И–Є–Љ
–њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П–Љ –Ї–≤–∞–љ—В–Њ–≤—Л–µ —Г—А–Њ–≤–љ–Є —Н–љ–µ—А–≥–Є–Є."
–Ю–±—Л—З–љ–Њ –Ї–Њ–Љ–µ–љ—В–∞—В–Њ—А—Л –њ–µ—А–≤–Њ–є —А–∞–±–Њ—В—Л –®—А–µ–і–Є–љ–≥–µ—А–∞ —Г–і–µ–ї—П—О—В –Љ–∞–ї–Њ –≤–љ–Є–Љ–∞–љ–Є—П
–і–∞–љ–љ–Њ–Љ—Г –і–Њ–±–∞–≤–ї–µ–љ–Є—О. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ, –њ–Њ–і–Њ–±–љ–Њ–µ –њ—А–µ–љ–µ–±—А–µ–ґ–µ–љ–Є–µ –њ—А–Њ–Є—Б—В–µ–Ї–∞–µ—В
–Є–Ј —В–Њ–≥–Њ, —З—В–Њ –љ–Є –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ (11), –љ–Є –і–∞–ґ–µ –Ї–ї—О—З–µ–≤–∞—П
–і–ї—П –њ–Њ–љ–Є–Љ–∞–љ–Є—П –≤—Б–µ–є —А–∞–±–Њ—В—Л –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –њ—А–Њ–±–ї–µ–Љ–∞ (6) –љ–Є–Ї–Њ–≥–і–∞
–±–Њ–ї—М—И–µ –љ–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є—Б—М –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –і–ї—П –Њ–±–Њ—Б–љ–Њ–≤–∞–љ–Є—П –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є.
–Э–∞—З–Є–љ–∞—П —Б–Њ —Б–ї–µ–і—Г—О—Й–µ–є —А–∞–±–Њ—В—Л –Є—Е –Љ–µ—Б—В–Њ –њ—А–Њ—З–љ–Њ –Ј–∞–є–Љ—Г—В –≤–Њ–ї–љ—Л –Љ–∞—В–µ—А–Є–Є
–і–µ –С—А–Њ–є–ї—П –Є –Њ–њ—В–Є–Ї–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–∞—П –∞–љ–∞–ї–Њ–≥–Є—П –У–∞–Љ–Є–ї—М—В–Њ–љ–∞. –Ю–і–љ–∞–Ї–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ
–Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ –≤ —Г–Ї–∞–Ј–∞–љ–Њ–Љ –і–Њ–±–∞–≤–ї–µ–љ–Є–Є, –њ–Њ —Б—Г—Й–µ—Б—В–≤—Г, –Ј–∞–ї–Њ–ґ–µ–љ–Њ –њ—А–∞–≤–Є–ї–Њ
–≤—Л—З–Є—Б–ї–µ–љ–Є—П —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П –і–ї—П –ї—О–±–Њ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –≤–µ–ї–Є—З–Є–љ—Л –њ–Њ
—Б–Њ—Б—В–Њ—П–љ–Є—О 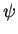 –Є –≤–≤–µ–і–µ–љ—Л –Њ–њ–µ—А–∞—В–Њ—А—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є –Є–Љ–њ—Г–ї—М—Б–∞ –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л
–і–ї—П —Б–ї—Г—З–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ,
–µ—Б–ї–Є –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П –≥–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ–Њ–Љ
–Є –≤–≤–µ–і–µ–љ—Л –Њ–њ–µ—А–∞—В–Њ—А—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є –Є–Љ–њ—Г–ї—М—Б–∞ –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л
–і–ї—П —Б–ї—Г—З–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ,
–µ—Б–ї–Є –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П –≥–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ–Њ–Љ
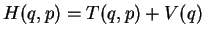 ,
—В–Њ –њ–µ—А–µ—Е–Њ–і –Ї –Њ–њ–Є—Б–∞–љ–Є—О –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л, –Ї–∞–Ї —Н—В–Њ —Б–ї–µ–і—Г–µ—В –Є–Ј —П–≤–љ–Њ–≥–Њ –≤–Є–і–∞
"–Є–љ—В–µ–≥—А–∞–ї–∞ –У–∞–Љ–Є–ї—М—В–Њ–љ–∞" (11), –Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –њ—А–Є –њ–Њ–Љ–Њ—Й–Є —Б–ї–µ–і—Г—О—Й–µ–є
–Ј–∞–Љ–µ–љ—Л:
,
—В–Њ –њ–µ—А–µ—Е–Њ–і –Ї –Њ–њ–Є—Б–∞–љ–Є—О –Ї–≤–∞–љ—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ—Л, –Ї–∞–Ї —Н—В–Њ —Б–ї–µ–і—Г–µ—В –Є–Ј —П–≤–љ–Њ–≥–Њ –≤–Є–і–∞
"–Є–љ—В–µ–≥—А–∞–ї–∞ –У–∞–Љ–Є–ї—М—В–Њ–љ–∞" (11), –Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –њ—А–Є –њ–Њ–Љ–Њ—Й–Є —Б–ї–µ–і—Г—О—Й–µ–є
–Ј–∞–Љ–µ–љ—Л:
| –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–µ –Њ–њ–Є—Б–∞–љ–Є–µ |
 |
–Ъ–≤–∞–љ—В–Њ–≤–Њ–µ –Њ–њ–Є—Б–∞–љ–Є–µ |
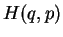 |
 |
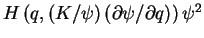 . . |
–≠—В–∞ –Ј–∞–Љ–µ–љ–∞ –≤—Л–њ–Њ–ї–љ—П–µ—В —В—Г –ґ–µ —Д—Г–љ–Ї—Ж–Є—О, —З—В–Њ –Є –Ј–∞–Љ–µ–љ–∞ –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е
(3) –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ —В–µ–Ї—Б—В–µ —Б—В–∞—В—М–Є, –љ–Њ –њ—А–Є —Н—В–Њ–Љ –љ–µ —В—А—Г–±—Г–µ—В,
—З—В–Њ–±—Л —Д—Г–љ–Ї—Ж–Є—П 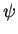 –±—Л–ї–∞ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–є. –Ш–Ј –і–∞–љ–љ–Њ–є
–Ј–∞–Љ–µ–љ—Л —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г –Є–Љ–њ—Г–ї—М—Б—Г
–±—Л–ї–∞ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ–є. –Ш–Ј –і–∞–љ–љ–Њ–є
–Ј–∞–Љ–µ–љ—Л —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г –Є–Љ–њ—Г–ї—М—Б—Г 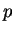 –≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ —Б–ї—Г—З–∞–µ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Њ–њ–µ—А–∞—В–Њ—А, –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л–є
–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ —Б–ї—Г—З–∞–µ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Њ–њ–µ—А–∞—В–Њ—А, –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л–є
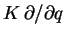 .
–Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –Ј–∞—Д–Є–Ї—Б–Є—А–Њ–≤–∞—В—М —В–Њ—З–љ–Њ, –µ—Б–ї–Є
–Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ –Ї–Њ–Љ—Г—В–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П
–Љ–µ–ґ–і—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є –Є –Є–Љ–њ—Г–ї—М—Б–Њ–Љ. –Ы–Њ–≥–Є—З–љ–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ –Ї –Љ–Њ–Љ–µ–љ—В—Г
–≤–љ–µ—Б–µ–љ–Є—П –і–Њ–њ–Њ–ї–љ–µ–љ–Є—П –≤ –Ї–Њ—А—А–µ–Ї—В—Г—А—Г –®—А–µ–і–Є–љ–≥–µ—А —Г–ґ–µ –Ј–љ–∞–ї –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П
–Њ–њ–µ—А–∞—В–Њ—А–∞ –Є–Љ–њ—Г–ї—М—Б–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –µ–≥–Њ —Б—В–∞—В—М—П "–Ю–± –Њ—В–љ–Њ—И–µ–љ–Є–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞ –Ї –Љ–Њ–µ–є", –≤ –Ї–Њ—В–Њ—А–Њ–є –Њ–љ –µ–≥–Њ –≤—Л–њ–Є—Б–∞–ї —П–≤–љ–Њ,
–њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О "Annalen der Physik" 18 –Љ–∞—А—В–∞ 1926 –≥–Њ–і–∞, —В–Њ –µ—Б—В—М
—З–µ—А–µ–Ј –њ–Њ–ї –Љ–µ—Б—П—Ж–∞ –њ–Њ—Б–ї–µ –≤–љ–µ—Б–µ–љ–Є—П –і–Њ–±–∞–≤–ї–µ–љ–Є–є –Ї –Њ–±—Б—Г–ґ–і–∞–µ–Љ–Њ–є —Б—В–∞—В—М–µ.
.
–Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –Ј–∞—Д–Є–Ї—Б–Є—А–Њ–≤–∞—В—М —В–Њ—З–љ–Њ, –µ—Б–ї–Є
–Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ –Ї–Њ–Љ—Г—В–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П
–Љ–µ–ґ–і—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В–Њ–є –Є –Є–Љ–њ—Г–ї—М—Б–Њ–Љ. –Ы–Њ–≥–Є—З–љ–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ –Ї –Љ–Њ–Љ–µ–љ—В—Г
–≤–љ–µ—Б–µ–љ–Є—П –і–Њ–њ–Њ–ї–љ–µ–љ–Є—П –≤ –Ї–Њ—А—А–µ–Ї—В—Г—А—Г –®—А–µ–і–Є–љ–≥–µ—А —Г–ґ–µ –Ј–љ–∞–ї –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П
–Њ–њ–µ—А–∞—В–Њ—А–∞ –Є–Љ–њ—Г–ї—М—Б–∞, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –µ–≥–Њ —Б—В–∞—В—М—П "–Ю–± –Њ—В–љ–Њ—И–µ–љ–Є–Є –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞-–С–Њ—А–љ–∞-–Ш–Њ—А–і–∞–љ–∞ –Ї –Љ–Њ–µ–є", –≤ –Ї–Њ—В–Њ—А–Њ–є –Њ–љ –µ–≥–Њ –≤—Л–њ–Є—Б–∞–ї —П–≤–љ–Њ,
–њ–Њ—Б—В—Г–њ–Є–ї–∞ –≤ —А–µ–і–∞–Ї—Ж–Є—О "Annalen der Physik" 18 –Љ–∞—А—В–∞ 1926 –≥–Њ–і–∞, —В–Њ –µ—Б—В—М
—З–µ—А–µ–Ј –њ–Њ–ї –Љ–µ—Б—П—Ж–∞ –њ–Њ—Б–ї–µ –≤–љ–µ—Б–µ–љ–Є—П –і–Њ–±–∞–≤–ї–µ–љ–Є–є –Ї –Њ–±—Б—Г–ґ–і–∞–µ–Љ–Њ–є —Б—В–∞—В—М–µ.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤–∞—А–Є–∞—Ж–Є—П "–Є–љ—В–µ–≥—А–∞–ї–∞ –У–∞–Љ–Є–ї—М—В–Њ–љ–∞" (11) (–®—А–µ–і–Є–љ–≥–µ—А
–љ–µ –Ј—А—П –њ–Њ—Б—В–∞–≤–Є–ї —Н—В–Є —Б–ї–Њ–≤–∞ –≤ –Ї–∞–≤—Л—З–Ї–Є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Б—В–Њ—П—Й–µ–µ –≤
(11) –њ–Њ–і –Ј–љ–∞–Ї–Њ–Љ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –≤—Л—А–∞–ґ–µ–љ–Є–µ –Є–Љ–µ–µ—В —Б—В–Њ–ї—М –ґ–µ –Љ–∞–ї–Њ–µ
–Њ—В–љ–Њ—И–µ–љ–Є–µ –Ї –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ—Г –У–∞–Љ–Є–ї—М—В–Њ–љ–Є–∞–љ—Г —Б–Ї–Њ–ї—М –Є —Г—А–∞–≤–љ–µ–љ–Є–µ (8) –Ї
"–њ–Њ—А–Њ–і–Є–≤—И–µ–Љ—Г" –µ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—О –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є (4)) –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В
—Б–Њ–±–Њ–є —Г—Б–ї–Њ–≤–Є–µ —В–Њ–≥–Њ, —З—В–Њ —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ–Њ–ї–љ–Њ–є —Н–љ–µ—А–≥–Є–Є, –≤—Л—З–Є—Б–ї–µ–љ–љ–Њ–є
–њ—А–Є –њ–Њ–Љ–Њ—Й–Є —Д—Г–љ–Ї—Ж–Є–Є 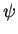 , –њ—А–Є–љ–Є–Љ–∞–µ—В —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —Б–Њ–≤–Љ–µ—Б—В–Є–Љ–Њ–µ
—Б —Г—Б–ї–Њ–≤–Є–µ–Љ –љ–Њ—А–Љ–Є—А–Њ–≤–Ї–Є (12), —В–Њ –µ—Б—В—М
, –њ—А–Є–љ–Є–Љ–∞–µ—В —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —Б–Њ–≤–Љ–µ—Б—В–Є–Љ–Њ–µ
—Б —Г—Б–ї–Њ–≤–Є–µ–Љ –љ–Њ—А–Љ–Є—А–Њ–≤–Ї–Є (12), —В–Њ –µ—Б—В—М
–≥–і–µ –Ј–љ–∞—З–Ї–Є  –Є
–Є  —Г–Ї–∞–Ј—Л–≤–∞—О—В, –≤ –Ї–∞–Ї–Њ–Љ
–љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є –і–µ–є—Б—В–≤—Г—О—В –Њ–њ–µ—А–∞—В–Њ—А—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є—П.
–Т–Њ–Ј–љ–Є–Ї–∞–µ—В —В–Є–њ–Є—З–љ–Њ–µ –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Б–Њ —Б–≤—П–Ј—П–Љ–Є, –Ї–Њ—В–Њ—А–Њ–µ
—Б—В–∞–љ–і–∞—А—В–љ–Њ —А–µ—И–∞–µ—В—Б—П –≤–≤–µ–і–µ–љ–Є–µ–Љ –Љ–љ–Њ–ґ–Є—В–µ–ї—П –Ы–∞–≥—А–∞–љ–ґ–∞, —З—В–Њ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ
—А–µ—И–µ–љ–Є—О —Г—А–∞–≤–љ–µ–љ–Є—П (8) c –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ
—Г–Ї–∞–Ј—Л–≤–∞—О—В, –≤ –Ї–∞–Ї–Њ–Љ
–љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є –і–µ–є—Б—В–≤—Г—О—В –Њ–њ–µ—А–∞—В–Њ—А—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є—П.
–Т–Њ–Ј–љ–Є–Ї–∞–µ—В —В–Є–њ–Є—З–љ–Њ–µ –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Б–Њ —Б–≤—П–Ј—П–Љ–Є, –Ї–Њ—В–Њ—А–Њ–µ
—Б—В–∞–љ–і–∞—А—В–љ–Њ —А–µ—И–∞–µ—В—Б—П –≤–≤–µ–і–µ–љ–Є–µ–Љ –Љ–љ–Њ–ґ–Є—В–µ–ї—П –Ы–∞–≥—А–∞–љ–ґ–∞, —З—В–Њ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ
—А–µ—И–µ–љ–Є—О —Г—А–∞–≤–љ–µ–љ–Є—П (8) c –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ 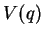 .
.
–І—В–Њ –µ—Й–µ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ —Б–і–µ–ї–∞–љ–Њ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ –≤ –њ–µ—А–≤–Њ–є —А–∞–±–Њ—В–µ? –Я–Њ—З—В–Є –љ–∞
–і–µ–≤—П—В–Є —Б—В—А–∞–љ–Є—Ж–∞—Е –®—А–µ–і–Є–љ–≥–µ—А –њ—А–Њ–≤–Њ–і–Є—В –∞–љ–∞–ї–Є–Ј —Г—А–∞–≤–љ–µ–љ–Є—П (8)
–≤ –њ–Њ–ї—П—А–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Ї–∞–Ї –њ—А–Є 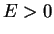 , —В–∞–Ї –Є –њ—А–Є
, —В–∞–Ї –Є –њ—А–Є 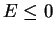 . –Ь—Л –љ–µ
–±—Г–і–µ–Љ –µ–≥–Њ –Ј–і–µ—Б—М –њ–Њ–і—А–Њ–±–љ–Њ –≤–Њ—Б–њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—М, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –і–∞–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј –Љ–Њ–ґ–љ–Њ
–љ–∞–є—В–Є –≤ –ї—О–±–Њ–Љ —Г—З–µ–±–љ–Є–Ї–µ –њ–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, –љ–∞–њ—А–Є–Љ–µ—А, –≤ [10].
–®—А–µ–і–Є–љ–≥–µ—А —Г—Б—В–∞–љ–Њ–≤–Є–ї, —З—В–Њ –≤ —Б–ї—Г—З–∞–µ
. –Ь—Л –љ–µ
–±—Г–і–µ–Љ –µ–≥–Њ –Ј–і–µ—Б—М –њ–Њ–і—А–Њ–±–љ–Њ –≤–Њ—Б–њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—М, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –і–∞–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј –Љ–Њ–ґ–љ–Њ
–љ–∞–є—В–Є –≤ –ї—О–±–Њ–Љ —Г—З–µ–±–љ–Є–Ї–µ –њ–Њ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ, –љ–∞–њ—А–Є–Љ–µ—А, –≤ [10].
–®—А–µ–і–Є–љ–≥–µ—А —Г—Б—В–∞–љ–Њ–≤–Є–ї, —З—В–Њ –≤ —Б–ї—Г—З–∞–µ 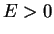 —Б–њ–µ–Ї—В—А –љ–Њ—Б–Є—В –љ–µ–њ—А–µ—А—Л–≤–љ—Л–є —Е–∞—А–∞–Ї—В–µ—А,
–∞ –≤ c–ї—Г—З–∞–µ
—Б–њ–µ–Ї—В—А –љ–Њ—Б–Є—В –љ–µ–њ—А–µ—А—Л–≤–љ—Л–є —Е–∞—А–∞–Ї—В–µ—А,
–∞ –≤ c–ї—Г—З–∞–µ 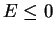 –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –Ј–∞–і–∞—З–∞ –Є–Љ–µ–µ—В —А–µ—И–µ–љ–Є—П —В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞,
–Ї–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є–µ
–≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–∞—П –Ј–∞–і–∞—З–∞ –Є–Љ–µ–µ—В —А–µ—И–µ–љ–Є—П —В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞,
–Ї–Њ–≥–і–∞ –Ј–љ–∞—З–µ–љ–Є–µ 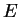 —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—Б–ї–Њ–≤–Є—О
—Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—Б–ї–Њ–≤–Є—О
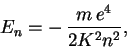 |
(13) |
–≥–і–µ 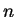 -–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–µ —Ж–µ–ї–Њ–µ —З–Є—Б–ї–Њ. –Ш–Ј —Б—А–∞–≤–љ–µ–љ–Є—П (13) –Є
—Б–њ–µ–Ї—В—А–∞, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ –Э.–С–Њ—А–Њ–Љ –і–ї—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞, –®—А–µ–і–Є–љ–≥–µ—А –Ј–∞–Ї–ї—О—З–∞–µ—В,
—З—В–Њ
-–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–µ —Ж–µ–ї–Њ–µ —З–Є—Б–ї–Њ. –Ш–Ј —Б—А–∞–≤–љ–µ–љ–Є—П (13) –Є
—Б–њ–µ–Ї—В—А–∞, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ –Э.–С–Њ—А–Њ–Љ –і–ї—П –∞—В–Њ–Љ–∞ –≤–Њ–і–Њ—А–Њ–і–∞, –®—А–µ–і–Є–љ–≥–µ—А –Ј–∞–Ї–ї—О—З–∞–µ—В,
—З—В–Њ 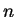 –Љ–Њ–ґ–љ–Њ –Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б –≥–ї–∞–≤–љ—Л–Љ –Ї–≤–∞–љ—В–Њ–≤—Л–Љ —З–Є—Б–ї–Њ–Љ (–≤–≤–µ–і–µ–љ—Л–Љ
–С–Њ—А–Њ–Љ –µ—Й–µ –≤ 1913 –≥–Њ–і—Г), –µ—Б–ї–Є –њ–Њ–ї–Њ–ґ–Є—В—М
–Љ–Њ–ґ–љ–Њ –Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б –≥–ї–∞–≤–љ—Л–Љ –Ї–≤–∞–љ—В–Њ–≤—Л–Љ —З–Є—Б–ї–Њ–Љ (–≤–≤–µ–і–µ–љ—Л–Љ
–С–Њ—А–Њ–Љ –µ—Й–µ –≤ 1913 –≥–Њ–і—Г), –µ—Б–ї–Є –њ–Њ–ї–Њ–ґ–Є—В—М 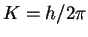 . –Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П
–њ–Њ—Б—В–Њ—П–љ–љ–∞—П
. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П
–њ–Њ—Б—В–Њ—П–љ–љ–∞—П 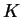 –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ –њ–µ—А–µ—З–µ—А–Ї–љ—Г—В–Њ–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –Я–ї–∞–љ–Ї–∞ –Є–ї–Є
–і–Є—А–∞–Ї–Њ–≤—Б–Ї–Њ–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –Є –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П
–љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ –њ–µ—А–µ—З–µ—А–Ї–љ—Г—В–Њ–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –Я–ї–∞–љ–Ї–∞ –Є–ї–Є
–і–Є—А–∞–Ї–Њ–≤—Б–Ї–Њ–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є –Є –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П 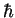 . –Ф–∞–ї–µ–µ –≤ —А–∞–±–Њ—В–µ
–њ—А–Є–≤–Њ–і–Є—В—Б—П –Њ–±—Й–∞—П —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П —А–∞–і–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є
. –Ф–∞–ї–µ–µ –≤ —А–∞–±–Њ—В–µ
–њ—А–Є–≤–Њ–і–Є—В—Б—П –Њ–±—Й–∞—П —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П —А–∞–і–Є–∞–ї—М–љ–Њ–є —З–∞—Б—В–Є –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є
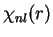 , –Є –Є—Б—Б–ї–µ–і—Г–µ—В—Б—П –Ї—А–∞—В–љ–Њ—Б—В—М –≤—Л—А–Њ–ґ–і–µ–љ–Є—П
, –Є –Є—Б—Б–ї–µ–і—Г–µ—В—Б—П –Ї—А–∞—В–љ–Њ—Б—В—М –≤—Л—А–Њ–ґ–і–µ–љ–Є—П 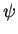 –њ–Њ
–њ–Њ  –Є
–Є 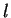 :
"–Я–Њ–і—Б—З–µ—В —З–Є—Б–ї–∞ –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е –≤ —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –љ–∞–є–і–µ–љ–Њ–µ
—А–µ—И–µ–љ–Є–µ —Б–Њ–і–µ—А–ґ–Є—В –њ—А–Є –і–Њ–њ—Г—Б—В–Є–Љ—Л—Е –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П—Е (
:
"–Я–Њ–і—Б—З–µ—В —З–Є—Б–ї–∞ –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е –≤ —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –љ–∞–є–і–µ–љ–Њ–µ
—А–µ—И–µ–љ–Є–µ —Б–Њ–і–µ—А–ґ–Є—В –њ—А–Є –і–Њ–њ—Г—Б—В–Є–Љ—Л—Е –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П—Е ( ,
,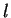 ) —А–Њ–≤–љ–Њ
) —А–Њ–≤–љ–Њ 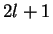 –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е; –њ—А–Є –Ј–∞–і–∞–љ–љ–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–Є
–њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е; –њ—А–Є –Ј–∞–і–∞–љ–љ–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–Є 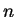 —З–Є—Б–ї–Њ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е
–њ–Њ—Б—В–Њ—П–љ–љ—Л—Е —А–∞–≤–љ–Њ, —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,
—З–Є—Б–ї–Њ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е
–њ–Њ—Б—В–Њ—П–љ–љ—Л—Е —А–∞–≤–љ–Њ, —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, 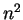 ". –Х—Б–ї–Є –ґ–µ —Г—З–µ—Б—В—М —Б–њ–Є–љ —Н–ї–µ–Ї—В—А–Њ–љ–∞,
–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤ –Ї–Њ–љ—Ж–µ 1925 - –љ–∞—З–µ–ї–µ 1926 –≥–Њ–і–∞ –±—Л–ї–Њ –љ–µ
–Є–Ј–≤–µ—Б—В–љ–Њ, —В–Њ –Ї—А–∞—В–љ–Њ—Б—В—М –≤—Л—А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–ґ–і–Њ–≥–Њ —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Г—А–Њ–≤–љ—П
". –Х—Б–ї–Є –ґ–µ —Г—З–µ—Б—В—М —Б–њ–Є–љ —Н–ї–µ–Ї—В—А–Њ–љ–∞,
–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–≥–Њ –≤ –Ї–Њ–љ—Ж–µ 1925 - –љ–∞—З–µ–ї–µ 1926 –≥–Њ–і–∞ –±—Л–ї–Њ –љ–µ
–Є–Ј–≤–µ—Б—В–љ–Њ, —В–Њ –Ї—А–∞—В–љ–Њ—Б—В—М –≤—Л—А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–ґ–і–Њ–≥–Њ —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Г—А–Њ–≤–љ—П 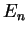 –±—Г–і–µ—В —А–∞–≤–љ–∞
–±—Г–і–µ—В —А–∞–≤–љ–∞ 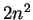 . –Т —Н—В–Њ–Љ –Љ–µ—Б—В–µ –≤–Њ –≤—В–Њ—А–Њ–є –Є –њ–Њ—Б–ї–µ–і–љ–Є–є —А–∞–Ј –≤ —А–∞–±–Њ—В–µ
–њ–Њ—П–≤–ї—П–µ—В—Б—П —Г–њ–Њ–Љ–Є–љ–∞–љ–Є–µ –Њ —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е, –љ–Њ –Њ–њ—П—В—М –њ–Њ –љ–µ–њ–Њ–љ—П—В–љ–Њ–є –њ—А–Є—З–Є–љ–µ
–љ–µ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ –њ—А–Є
. –Т —Н—В–Њ–Љ –Љ–µ—Б—В–µ –≤–Њ –≤—В–Њ—А–Њ–є –Є –њ–Њ—Б–ї–µ–і–љ–Є–є —А–∞–Ј –≤ —А–∞–±–Њ—В–µ
–њ–Њ—П–≤–ї—П–µ—В—Б—П —Г–њ–Њ–Љ–Є–љ–∞–љ–Є–µ –Њ —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е, –љ–Њ –Њ–њ—П—В—М –њ–Њ –љ–µ–њ–Њ–љ—П—В–љ–Њ–є –њ—А–Є—З–Є–љ–µ
–љ–µ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ –њ—А–Є 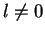 —Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–≥—Г—В –Њ–Ї–∞–Ј–∞—В—М—Б—П
–Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л–Љ–Є.
—Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–≥—Г—В –Њ–Ї–∞–Ј–∞—В—М—Б—П
–Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л–Љ–Є.
–Я–Њ–Ј–≤–Њ–ї–Є–Љ —Б–µ–±–µ –њ—А–µ–і–ї–Њ–ґ–Є—В—М –≤–љ–Є–Љ–∞–љ–Є—О —З–Є—В–∞—В–µ–ї–µ–є –Њ–і–љ—Г –≥–Є–њ–Њ—В–µ–Ј—Г. –Ю–љ–∞
–і–Њ—Б—В–∞—В–Њ—З–љ–Њ –ї–Њ–≥–Є—З–љ–∞, –Њ–і–љ–∞–Ї–Њ –љ–∞–і–Њ —Б–Ї–∞–Ј–∞—В—М –њ—А—П–Љ–Њ, —З—В–Њ –њ–Њ–і—В–≤–µ—А–ґ–і–∞—О—Й–Є—Е
–µ–µ —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤ –ї–Є–±–Њ –љ–µ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ –≤–Њ–≤—Б–µ, –ї–Є–±–Њ –Њ–љ–Є –љ–µ —Б–Њ—Е—А–∞–љ–Є–ї–Є—Б—М.
–Т–Њ–Ј–Љ–Њ–ґ–љ–Њ, —З—В–Њ –Ї–ї—О—З –Ї –Њ—В–≤–µ—В—Г –љ–∞ –≤–Њ–њ—А–Њ—Б, –њ–Њ—З–µ–Љ—Г –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ—Б—В—М —И–∞—А–Њ–≤—Л—Е
—Д—Г–љ–Ї—Ж–Є–є –±—Л–ї–∞ –њ—А–Њ–Є–≥–љ–Њ—А–Є—А–Њ–≤–∞–љ–∞ –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ,
–ї–µ–ґ–Є—В –≤ –Љ–∞–ї–µ–љ—М–Ї–Њ–є —Б—Б—Л–ї–Ї–µ, –Ї–Њ—В–Њ—А–∞—П –њ—А–µ–і–≤–∞—А—П–µ—В –∞–љ–∞–ї–Є–Ј —А–µ—И–µ–љ–Є–є —Г—А–∞–≤–љ–µ–љ–Є—П
(8): "–ѓ –У–ї—Г–±–Њ–Ї–Њ –±–ї–∞–≥–Њ–і–∞—А–µ–љ –У–µ—А–Љ–∞–љ—Г –Т–µ–є–ї—О –Ј–∞ –µ–≥–Њ –њ–Њ–Љ–Њ—Й—М –њ—А–Є
—А–µ—И–µ–љ–Є–Є —Г—А–∞–≤–љ–µ–љ–Є—П (8)". –Т–њ–Њ–ї–љ–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, —Н—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ
–®—А–µ–і–Є–љ–≥–µ—А —Г–Ј–љ–∞–ї —Г –Т–µ–є–ї—П –љ–µ–Ї–Њ—В–Њ—А—Л–µ –Љ–Є–љ–Є–Љ–∞–ї—М–љ—Л–µ –Њ—Б–љ–Њ–≤–љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П –Њ
—И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є—П—Е (—А–µ–Ј—Г–ї—М—В–∞—В –і–µ–є—Б—В–≤–Є—П –љ–∞ –љ–Є—Е –Њ–њ–µ—А–∞—В–Њ—А–∞ –Ы–∞–њ–ї–∞—Б–∞ –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е
–Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е, –Ї—А–∞—В–љ–Њ—Б—В—М –≤—Л—А–Њ–ґ–і–µ–љ–Є—П, –љ–Њ—А–Љ–Є—А–Њ–≤–Ї—Г), –Ї–Њ—В–Њ—А—Л–µ –њ–Њ–Љ–Њ–≥–ї–Є
–µ–Љ—Г —А–µ—И–Є—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ (8), –љ–Њ –≥–ї—Г–±–Њ–Ї–Њ —Б —В–µ–Њ—А–Є–µ–є —Н—В–Є—Е —Д—Г–љ–Ї—Ж–Є–є
–љ–µ —А–∞–Ј–±–Є—А–∞–ї—Б—П. –Ю—В—Б—О–і–∞ –Є –Њ—В—Б—Г—В—Б—В–≤–Є–µ —П–≤–љ–Њ–≥–Њ –≤–Є–і–∞ —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є
–≤ —В–µ–Ї—Б—В–µ —Б—В–∞—В—М–Є, –Є –љ–µ–Ј–љ–∞–љ–Є–µ —В–Њ–≥–Њ, —З—В–Њ —И–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Љ–Њ–≥—Г—В –Њ–Ї–∞–Ј–∞—В—М—Б—П
–Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л–Љ–Є.
–®—А–µ–і–Є–љ–≥–µ—А –љ–µ —Б–Љ–Њ–≥ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –љ–∞–є–і–µ–љ—Л–є –Є–Љ –љ–∞–±–Њ—А —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є
–Є —Б–Њ–±—Б—В–≤–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є —Г—А–∞–≤–љ–µ–љ–Є—П (8) —П–≤–ї—П–µ—В—Б—П –њ–Њ–ї–љ—Л–Љ. –Ю–і–љ–∞–Ї–Њ
–Њ–љ –њ–Њ–і—З–µ—А–Ї–љ—Г–ї, —З—В–Њ "—Б–Њ–≥–ї–∞—Б–љ–Њ –і—А—Г–≥–Є–Љ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П–Љ –Љ–Њ–ґ–љ–Њ
–њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є—В—М, —З—В–Њ –Љ—Л –љ–µ –њ—А–Њ–њ—Г—Б—В–Є–ї–Є –Ї–∞–Ї–Њ–≥–Њ-–ї–Є–±–Њ —Б–Њ–±—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П".
–°—В—А–Њ–≥–Њ–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ –і–∞–љ–љ–Њ–≥–Њ —Д–∞–Ї—В–∞ –±—Л–ї–Њ –і–∞–љ–Њ –Р—А—В—Г—А–Њ–Љ –≠–і–і–Є–љ–≥—В–Њ–љ–Њ–Љ
–≤ 1927 –≥–Њ–і—Г.
–Ґ–∞–Ї —З—В–Њ –ґ–µ, –љ–µ—Б–Љ–Њ—В—А—П –љ–∞ –≤—Б–µ –ї–Њ–≥–Є—З–µ—Б–Ї–Є–µ –њ—А–Њ—В–Є–≤–Њ–Њ—А–µ—З–Є—П –Є –њ—А—П–Љ—Л–µ –Њ—И–Є–±–Ї–Є,
–Ј–∞—Б—В–∞–≤–Є–ї–Њ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Є–Ї–Њ–≤ —Б–∞–Љ—Л–Љ –≤–Њ—Б—В–Њ—А–ґ–µ–љ–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Њ—В–љ–µ—Б—В–Є—Б—М –Ї
–Ј–∞—А–Њ–ґ–і–∞—О—Й–µ–є—Б—П –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –љ–∞—З–Є–љ–∞—П —Г–ґ–µ —Б –њ–µ—А–≤–є –љ–µ –Њ—З–µ–љ—М —Г–і–∞—З–љ–Њ–є —Б—В–∞—В—М–Є
–≠.–®—А–µ–і–Є–љ–≥–µ—А–∞? –Т –Њ—Б–љ–Њ–≤–љ–Њ–Љ, –Ї–∞–Ї —Г–ґ–µ –Љ–љ–Њ–≥–Њ–Ї—А–∞—В–љ–Њ –Њ—В–Љ–µ—З–∞–ї—Б—М –≤—Л—И–µ, –µ–µ –Ї–∞–ґ—Г—Й–∞—П—Б—П
–Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–љ–Њ—Б—В—М –≤ –њ—А–Є–≤—Л—З–љ—Л–µ –њ–Њ–љ—П—В–Є—П —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є —В–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є:
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –У–∞–Љ–Є–ї—М—В–Њ–љ–∞-–ѓ–Ї–Њ–±–Є, –≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ—Л–є –њ—А–Є–љ—Ж–Є–њ,
–≤–Њ–Ј–љ–Є–Ї–љ–Њ–≤–µ–љ–Є–µ –і–Є—Б–Ї—А–µ—В–љ—Л—Е —Г—А–Њ–≤–љ–µ–є –≤ –∞—В–Њ–Љ–µ –≤–Њ–і–Њ—А–Њ–і–∞ –њ–Њ–і–Њ–±–љ–Њ —В–Њ–Љ—Г, "–Ї–∞–Ї
—Б–∞–Љ–∞ –њ–Њ —Б–µ–±–µ –њ–Њ–ї—Г—З–∞–µ—В—Б—П —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В—М —З–Є—Б–ї–∞ —Г–Ј–ї–Њ–≤ –њ—А–Є —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–Є
–Ї–Њ–ї–µ–±–ї—О—Й–µ–є—Б—П —Б—В—А—Г–љ—Л", –Ї–∞–ґ—Г—Й–µ–µ—Б—П –Њ—В—Б—Г—В—Б—В–≤–Є–µ —Н—В–Є—Е —Г–ґ–∞—Б–љ—Л—Е –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–Ї–∞—З–Ї–Њ–≤.
–Я–ї–∞–љ–Ї –њ–Є—Б–∞–ї –®—А–µ–і–Є–љ–≥–µ—А—Г –≤ –∞–њ—А–µ–ї–µ 1926 –≥–Њ–і–∞: "–І–Є—В–∞—О –Т–∞—И—Г —Б—В–∞—В—М—О —Б —В–µ–Љ –ґ–µ
–љ–∞–њ—А—П–ґ–µ–љ–Є–µ–Љ, —Б –Ї–∞–Ї–Є–Љ –ї—О–±–Њ–њ—Л—В–љ—Л–є —А–µ–±–µ–љ–Њ–Ї –≤—Л—Б–ї—Г—И–Є–≤–∞–µ—В —А–∞–Ј–≤—П–Ј–Ї—Г –Ј–∞–≥–∞–і–Ї–Є,
–љ–∞–і –Ї–Њ—В–Њ—А–Њ–є –Њ–љ –і–Њ–ї–≥–Њ –Љ—Г—З–Є–ї—Б—П, –Є —А–∞–і—Г—О—Б—М –Ї—А–∞—Б–Њ—В–∞–Љ, —А–∞—Б–Ї—А—Л–≤–∞—О—Й–Є–Љ—Б—П –њ–µ—А–µ–і
–Љ–Њ–Є–Љ–Є –≥–ї–∞–Ј–∞–Љ–Є". –Я–ї–∞–љ–Ї—Г –≤—В–Њ—А–Є—В –Ы–Њ—А–µ–љ—Ж: "... –і–∞–ґ–µ –µ—Б–ї–Є –Њ–Ї–∞–ґ–µ—В—Б—П, —З—В–Њ –љ–∞
—Н—В–Њ–Љ –њ—Г—В–Є –љ–µ —Г–і–∞—Б—В—Б—П –њ—А–Є–є—В–Є –Ї —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В–µ–ї—М–љ–Њ–Љ—Г —А–µ—И–µ–љ–Є—О, –≤—Б–µ –ґ–µ —Б–ї–µ–і—Г–µ—В
–≤–Њ—Б—Е–Є—Й–∞—В—М—Б—П –њ—А–Њ–љ–Є—Ж–∞—В–µ–ї—М–љ–Њ—Б—В—М—О –Т–∞—И–Є—Е —Б–Њ–Њ–±—А–∞–ґ–µ–љ–Є–є –Є –љ–∞–і–µ—П—В—М—Б—П, —З—В–Њ –Т–∞—И–Є
—Г—Б–Є–ї–Є—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –њ–Њ–Љ–Њ–≥—Г—В –≥–ї—Г–±–ґ–µ –њ—А–Њ–љ–Є–Ї–љ—Г—В—М –≤ —Н—В–Є –Ј–∞–≥–∞–і–Њ—З–љ—Л–µ
(–Ї–≤–∞–љ—В–Њ–≤—Л–µ - –Э.–Э.) —П–≤–ї–µ–љ–Є—П." –Э–∞–Ї–Њ–љ–µ—Ж, —А–µ–∞–Ї—Ж–Є—П –≠–є–љ—И—В–µ–є–љ–∞: "–У–Њ—Б–њ–Њ–і–Є–љ
–Я–ї–∞–љ–Ї —Б –Њ–њ—А–∞–≤–і–∞–љ–љ—Л–Љ –≤–Њ—Б—В–Њ—А–≥–Њ–Љ, –њ–Њ–Ї–∞–Ј–∞–ї –Љ–љ–µ –Т–∞—И—Г —В–µ–Њ—А–Є—О, –Ї–Њ—В–Њ—А—Г—О
—П —В–∞–Ї –ґ–µ —Б—В–∞–ї –Є–Ј—Г—З–∞—В—М —Б –Њ–≥—А–Њ–Љ–љ—Л–Љ –Є–љ—В–µ—А–µ—Б–Њ–Љ". –Ш –љ–µ–Ї–Њ—В–Њ—А–Њ–µ –≤—А–µ–Љ—П —Б–њ—Г—Б—В—П:
"–ѓ —Г–±–µ–ґ–і–µ–љ, —З—В–Њ –Т–∞—И–µ–є —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї–Њ–є —Г—Б–ї–Њ–≤–Є–є –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –Т—Л –і–Њ–±–Є–ї–Є—Б—М
—А–µ—И–∞—О—Й–µ–≥–Њ —Г—Б–њ–µ—Е–∞. –ѓ —В–∞–Ї –ґ–µ —Г–±–µ–ґ–і–µ–љ, —З—В–Њ –њ—Г—В—М, –Є–Ј–±—А–∞–љ–љ—Л–є –У–µ–є–Ј–µ–љ–±–µ—А–≥–Њ–Љ
–Є –С–Њ—А–љ–Њ–Љ, —Г–≤–Њ–і–Є—В –≤ —Б—В–Њ—А–Њ–љ—Г." –Р –≤–Њ—В, —З—В–Њ –њ–Є—И–µ—В –≤ —Б–≤–Њ–Є—Е –≤–Њ—Б–њ–Њ–Љ–Є–љ–∞–љ–Є—П—Е
[11] –Т.–У–µ–є–Ј–µ–љ–±–µ—А–≥: "...–Љ–µ—В–Њ–і–Є–Ї–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ–Ј–≤–Њ–ї—П–ї–∞
–Њ—Б—Г—Й–µ—Б—В–≤–Є—В—М —Ж–µ–ї—Л–є —А—П–і –≤—Л—З–Є—Б–ї–µ–љ–Є–є, –Ї–Њ—В–Њ—А—Л–µ –≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є (—В–Њ –µ—Б—В—М
–Љ–∞—В—А–Є—З–љ–Њ–є - –Э.–Э.) –Љ–µ—Е–∞–љ–Є–Ї–µ –±—Л–ї–Є –±—Л —З—А–µ–Ј–≤—Л—З–∞–є–љ–Њ —Б–ї–Њ–ґ–љ—Л–Љ–Є." –Р –Љ–љ–Њ–≥–Є–µ,
–Ї–∞–Ї, –љ–∞–њ—А–Є–Љ–µ—А, —Г–ґ–µ —Г–њ–Њ–Љ–Є–љ–∞–≤—И–Є–є—Б—П –Т.–Т–Є–љ, –љ–∞–њ—А—П–Љ—Г—О —Б–≤—П–Ј—Л–≤–∞–ї–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Г—О
–ї–µ–≥–Ї–Њ—Б—В—М –≤—Л—З–Є—Б–ї–µ–љ–Є–є –≤ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Љ–∞—В—А–Є—З–љ–Њ–є —Б —В–µ–Љ,
—З—В–Њ –≤–Њ–ї–љ–Њ–≤–∞—П –Љ–µ—Е–∞–љ–Є–Ї–∞ —П–≤–ї—П–µ—В—Б—П –±–Њ–ї–µ–µ –њ—А–∞–≤–Є–ї—М–љ–є —В–µ–Њ—А–Є–µ–є –і–ї—П –Њ–њ–Є—Б–∞–љ–Є—П
–Љ–Є–Ї—А–Њ–Љ–Є—А–∞.
–І—В–Њ –≤ –њ–µ—А–≤–Њ–є —Б—В–∞—В—М–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ —Ж–µ–љ–љ–Њ –і–ї—П –њ–Њ—В–Њ–Љ–Ї–Њ–≤?
–Я—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ - –≤ —Н—В–Њ–є —Б—В–∞—В—М–µ –≤–њ–µ—А–≤—Л–µ –њ–Њ—П–≤–ї—П–µ—В—Б—П —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ
–®—А–µ–і–Є–љ–≥–µ—А–∞. –Я—Г—Б—В—М –Њ–љ–Њ "–≤—Л–≤–µ–і–µ–љ–Њ" –∞–±—Б–Њ–ї—О—В–љ–Њ –љ–µ –ї–Њ–≥–Є—З–љ—Л–Љ, –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М,
–і–∞–ґ–µ –љ–µ–≤–µ—А–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ. –°–µ–≥–Њ–і–љ—П –Љ—Л –Ј–љ–∞–µ–Љ, —З—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –®—А–µ–і–Є–љ–≥–µ—А–∞ –Ї–Њ—А—А–µ–Ї—В–љ–Њ
–≤—Л–≤–µ—Б—В–Є –љ–µ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤–Њ–≤—Б–µ. –≠—В–Њ –Њ–і–Є–љ –Є–Ј –њ–Њ—Б—В—Г–ї–∞—В–Њ–≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є,
–њ–Њ–і–Њ–±–љ–Њ —В–Њ–Љ—Г, –Ї–∞–Ї –Ј–∞–Ї–Њ–љ—Л –Э—М—О—В–Њ–љ–∞ —П–≤–ї—П—О—В—Б—П –њ–Њ—Б—В—Г–ї–∞—В–∞–Љ–Є –Љ–µ—Е–∞–љ–Є–Ї–Є
–Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є. –≠—В–Њ –њ–µ—А–≤–Њ–µ. –Т—В–Њ—А–Њ–µ - –≤–њ–µ—А–≤—Л–µ –≤–≤–µ–і–µ–љ–Њ –њ–Њ–љ—П—В–Є–µ –≤–Њ–ї–љ–Њ–≤–Њ–є
—Д—Г–љ–Ї—Ж–Є–Є –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л 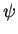 –Є —Б–і–µ–ї–∞–љ–∞ –њ–Њ–њ—Л—В–Ї–∞ –њ—А–Є–і–∞—В—М —Д—Г–љ–Ї—Ж–Є–Є
–Є —Б–і–µ–ї–∞–љ–∞ –њ–Њ–њ—Л—В–Ї–∞ –њ—А–Є–і–∞—В—М —Д—Г–љ–Ї—Ж–Є–Є 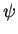 –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї. –Ш–Љ–µ–љ–љ–Њ –љ–∞—З–Є–љ–∞—П —Б —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Њ–є –љ–∞–Љ–Є —Б—В–∞—В—М–Є
–®—А–µ–і–Є–љ–≥–µ—А–∞, –≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –Њ–±—А–∞—В–Є–ї–Є –≤–љ–Є–Љ–∞–љ–Є—П –љ–µ —В–Њ–ї—М–Ї–Њ –љ–∞ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ
–Ј–љ–∞—З–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–≥–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Њ–њ–µ—А–∞—В–Њ—А–∞ (–Є–ї–Є –Љ–∞—В—А–Є—Ж—Л, –Ї–∞–Ї —Г
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –С–Њ—А–љ–∞ –Є –Ш–Њ—А–і–∞–љ–∞), –љ–Њ –Є –љ–∞ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –і–∞–љ–љ–Њ–≥–Њ
–Њ–њ–µ—А–∞—В–Њ—А–∞. –Ш –њ–Њ—Б–ї–µ–і–љ–µ–µ, –≤ —А–∞–±–Њ—В–µ –њ—А–Њ–≤–µ–і–µ–љ —Б—В–∞–≤—И–Є–є —В–µ–њ–µ—А—М –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ
–∞–љ–∞–ї–Є–Ј —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П —З–∞—Б—В–Є—Ж—Л –≤ —Ж–µ–љ—В—А–∞–ї—М–љ–Њ—Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–Љ
–њ–Њ–ї–µ. –≠—В–Њ—В –∞–љ–∞–ї–Є–Ј –≤–Њ—И–µ–ї —Б –љ–µ–±–Њ–ї—М—И–Є–Љ–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П–Љ–Є –≤–Њ –≤—Б–µ —Г—З–µ–±–љ–Є–Ї–Є –њ–Њ
–Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ.
–Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Л–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї. –Ш–Љ–µ–љ–љ–Њ –љ–∞—З–Є–љ–∞—П —Б —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Њ–є –љ–∞–Љ–Є —Б—В–∞—В—М–Є
–®—А–µ–і–Є–љ–≥–µ—А–∞, –≤ –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є –Њ–±—А–∞—В–Є–ї–Є –≤–љ–Є–Љ–∞–љ–Є—П –љ–µ —В–Њ–ї—М–Ї–Њ –љ–∞ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ
–Ј–љ–∞—З–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–≥–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Њ–њ–µ—А–∞—В–Њ—А–∞ (–Є–ї–Є –Љ–∞—В—А–Є—Ж—Л, –Ї–∞–Ї —Г
–У–µ–є–Ј–µ–љ–±–µ—А–≥–∞, –С–Њ—А–љ–∞ –Є –Ш–Њ—А–і–∞–љ–∞), –љ–Њ –Є –љ–∞ —Б–Њ–±—Б—В–≤–µ–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –і–∞–љ–љ–Њ–≥–Њ
–Њ–њ–µ—А–∞—В–Њ—А–∞. –Ш –њ–Њ—Б–ї–µ–і–љ–µ–µ, –≤ —А–∞–±–Њ—В–µ –њ—А–Њ–≤–µ–і–µ–љ —Б—В–∞–≤—И–Є–є —В–µ–њ–µ—А—М –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ
–∞–љ–∞–ї–Є–Ј —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П —З–∞—Б—В–Є—Ж—Л –≤ —Ж–µ–љ—В—А–∞–ї—М–љ–Њ—Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–Љ
–њ–Њ–ї–µ. –≠—В–Њ—В –∞–љ–∞–ї–Є–Ј –≤–Њ—И–µ–ї —Б –љ–µ–±–Њ–ї—М—И–Є–Љ–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П–Љ–Є –≤–Њ –≤—Б–µ —Г—З–µ–±–љ–Є–Ї–Є –њ–Њ
–Ї–≤–∞–љ—В–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ.
–Т —Б–≤—П–Ј–Є —Б –њ–Њ—Б–ї–µ–і–љ–Є–Љ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–і–µ–ї–∞—В—М –Њ–і–љ–Њ –Ј–∞–Љ–µ—З–∞–љ–Є–µ.
–Р–љ–∞–ї–Є–Ј —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–њ–µ–Ї—В—А–∞ —Г—А–∞–≤–љ–µ–љ–Є—П (8) –љ–µ –±—Л–ї –љ–Є
–Є–ї–ї—О—Б—В—А–∞—Ж–Є–µ–є –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–ї–Њ–ґ–µ–љ–Є–є —Г—А–∞–≤–љ–µ–љ–Є—П (8),
–љ–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ –њ—А–µ–і—Б–Ї–∞–Ј–∞–љ–Є–µ–Љ, –Ї–Њ—В–Њ—А–Њ–µ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Є–Ј
—А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П. –≠—В–Њ —Б–≤—П–Ј–∞–љ–Њ —Б —В–µ–Љ, —З—В–Њ –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є
–њ—А–Є—Б—Г—В—Б—В–≤—Г–µ—В –љ–µ–Є–Ј–≤–µ—Б—В–љ–∞—П –Ї–Њ–љ—Б—В–∞–љ—В–∞ 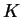 , –Ї–Њ—В–Њ—А–∞—П —Б–∞–Љ–∞ –њ–Њ —Б–µ–±–µ –љ—Г–ґ–і–∞–µ—В—Б—П
–≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є. –°—А–∞–≤–љ–µ–љ–Є–µ —Г—А–Њ–≤–љ–µ–є —Н–љ–µ—А–≥–Є–Є (13) —Б –Є–Ј–≤–µ—Б—В–љ—Л–Љ
—А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –С–Њ—А–∞ –Ї–∞–Ї —А–∞–Ј –Є —Д–Є–Ї—Б–Є—А—Г–µ—В –њ–Њ—Б—В–Њ—П–љ–љ—Г—О
, –Ї–Њ—В–Њ—А–∞—П —Б–∞–Љ–∞ –њ–Њ —Б–µ–±–µ –љ—Г–ґ–і–∞–µ—В—Б—П
–≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є. –°—А–∞–≤–љ–µ–љ–Є–µ —Г—А–Њ–≤–љ–µ–є —Н–љ–µ—А–≥–Є–Є (13) —Б –Є–Ј–≤–µ—Б—В–љ—Л–Љ
—А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –С–Њ—А–∞ –Ї–∞–Ї —А–∞–Ј –Є —Д–Є–Ї—Б–Є—А—Г–µ—В –њ–Њ—Б—В–Њ—П–љ–љ—Г—О 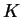 –≤ (8).
–Я—А–Є–Љ–µ—А—Л –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Є—Е —Б–њ–µ–Ї—В—А–Њ–≤ –і—А—Г–≥–Є—Е –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–Є—Б—В–µ–Љ
—Г–ґ–µ –њ—А–Є —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–Љ
–≤ (8).
–Я—А–Є–Љ–µ—А—Л –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —Н–љ–µ—А–≥–µ—В–Є—З–µ—Б–Ї–Є—Е —Б–њ–µ–Ї—В—А–Њ–≤ –і—А—Г–≥–Є—Е –Ї–≤–∞–љ—В–Њ–≤—Л—Е —Б–Є—Б—В–µ–Љ
—Г–ґ–µ –њ—А–Є —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–Љ 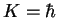 –Є —Б—А–∞–≤–љ–µ–љ–Є–µ –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е —В–∞–Ї–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ —Б–њ–µ–Ї—В—А–Њ–≤ —Б —А–∞—Б—З–Є—В–∞–љ–љ—Л–Љ–Є –і—А—Г–≥–Є–Љ–Є –Љ–µ—В–Њ–і–∞–Љ–Є –Є–ї–Є —Б —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–Љ
–≤ —А–∞–±–Њ—В–µ –Њ—В—Б—Г—В—Б—В–≤—Г—О—В. –≠—В–Њ –Ј–∞—Б—В–∞–≤–ї—П–µ—В –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ—А–Њ—П–≤–ї—П—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Г—О
–Њ—Б—В–Њ—А–Њ–ґ–љ–Њ—Б—В—М –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ –Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є —Б–≤–Њ–µ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П:
"–ѓ –љ–µ —Б—З–Є—В–∞—О –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ, –і–Њ —В–µ—Е –њ–Њ—А –њ–Њ–Ї–∞ –љ–µ –±—Г–і—Г—В —Г—Б–њ–µ—И–љ–Њ —А–∞—Б—Б—З–Є—В–∞–љ—Л
–љ–Њ–≤—Л–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–µ –Ј–∞–і–∞—З–Є, –њ–Њ–і—А–Њ–±–љ–µ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М
–Є—Б—В–Њ–ї–Ї–Њ–≤–∞–љ–Є–µ –≤–≤–µ–і–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Э–µ –Є—Б–Ї–ї—О—З–µ–љ–∞ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М,
—З—В–Њ –њ–Њ–і–Њ–±–љ—Л–µ —А–∞—Б—З–µ—В—Л –њ—А–Є–≤–µ–і—Г—В –Ї –њ—А–Њ—Б—В–Њ–Љ—Г —Б–Њ–≤–њ–∞–і–µ–љ–Є—О —Б –≤—Л–≤–Њ–і–∞–Љ–Є –Њ–±—Л—З–љ–Њ–є
–Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є (—В–Њ –µ—Б—В—М, —Б —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є, –њ–Њ–ї—Г—З–µ–љ–љ—Л–Љ–Є –њ—А–Є –њ–Њ–Љ–Њ—Й–Є
–њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ (1) - –Э.–Э.)." –Э–Њ
–њ—А–Є —Н—В–Њ–Љ –Љ—Л –і–Њ–ї–ґ–љ—Л –њ–Њ–Љ–љ–Є—В—М, —З—В–Њ –≥–ї–∞–≤–љ—Л–Љ –Њ–њ—А–∞–≤–і–∞–љ–Є–µ–Љ –≤–≤–µ–і–µ–љ–Є—П
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (8) –і–ї—П –®—А–µ–і–Є–љ–≥–µ—А–∞ —Б–ї—Г–ґ–Є—В —В–Њ,
—З—В–Њ –±–ї–∞–≥–Њ–і–∞—А—П —Н—В–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О —Г–і–∞–ї–Њ—Б—М –Є–Ј–±–∞–≤–Є—В—М—Б—П –Њ—В –Ј–∞–≥–∞–і–Њ—З–љ–Њ–≥–Њ
—В—А–µ–±–Њ–≤–∞–љ–Є—П —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є –≤ (1) –Є —В–µ–Љ —Б–∞–Љ—Л–Љ (–Њ–±–Љ–∞–љ—З–Є–≤–Њ
–ї–Њ–≥–Є—З–љ–Њ!) —Б–≤–µ—Б—В–Є –љ–µ–њ—А–Є–≤—Л—З–љ—Л–µ, –∞ –њ–Њ—В–Њ–Љ—Г –Ј–∞–≥–∞–і–Њ—З–љ—Л–µ, –Ј–∞–Ї–Њ–љ—Л –Љ–Є–Ї—А–Њ–Љ–Є—А–∞
–Ї –Є–Ј–≤–µ—Б—В–љ—Л–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –Ї–Њ–ї–µ–±–∞–љ–Є–є.
–Є —Б—А–∞–≤–љ–µ–љ–Є–µ –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е —В–∞–Ї–Є–Љ
–Њ–±—А–∞–Ј–Њ–Љ —Б–њ–µ–Ї—В—А–Њ–≤ —Б —А–∞—Б—З–Є—В–∞–љ–љ—Л–Љ–Є –і—А—Г–≥–Є–Љ–Є –Љ–µ—В–Њ–і–∞–Љ–Є –Є–ї–Є —Б —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–Љ
–≤ —А–∞–±–Њ—В–µ –Њ—В—Б—Г—В—Б—В–≤—Г—О—В. –≠—В–Њ –Ј–∞—Б—В–∞–≤–ї—П–µ—В –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ—А–Њ—П–≤–ї—П—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–љ—Г—О
–Њ—Б—В–Њ—А–Њ–ґ–љ–Њ—Б—В—М –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ –Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є —Б–≤–Њ–µ–≥–Њ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П:
"–ѓ –љ–µ —Б—З–Є—В–∞—О –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–Љ, –і–Њ —В–µ—Е –њ–Њ—А –њ–Њ–Ї–∞ –љ–µ –±—Г–і—Г—В —Г—Б–њ–µ—И–љ–Њ —А–∞—Б—Б—З–Є—В–∞–љ—Л
–љ–Њ–≤—Л–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–µ –Ј–∞–і–∞—З–Є, –њ–Њ–і—А–Њ–±–љ–µ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М
–Є—Б—В–Њ–ї–Ї–Њ–≤–∞–љ–Є–µ –≤–≤–µ–і–µ–љ–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞—В–µ–ї—М–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞. –Э–µ –Є—Б–Ї–ї—О—З–µ–љ–∞ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М,
—З—В–Њ –њ–Њ–і–Њ–±–љ—Л–µ —А–∞—Б—З–µ—В—Л –њ—А–Є–≤–µ–і—Г—В –Ї –њ—А–Њ—Б—В–Њ–Љ—Г —Б–Њ–≤–њ–∞–і–µ–љ–Є—О —Б –≤—Л–≤–Њ–і–∞–Љ–Є –Њ–±—Л—З–љ–Њ–є
–Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є (—В–Њ –µ—Б—В—М, —Б —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є, –њ–Њ–ї—Г—З–µ–љ–љ—Л–Љ–Є –њ—А–Є –њ–Њ–Љ–Њ—Й–Є
–њ—А–∞–≤–Є–ї–∞ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –С–Њ—А–∞-–Ч–Њ–Љ–Љ–µ—А—Д–µ–ї—М–і–∞ (1) - –Э.–Э.)." –Э–Њ
–њ—А–Є —Н—В–Њ–Љ –Љ—Л –і–Њ–ї–ґ–љ—Л –њ–Њ–Љ–љ–Є—В—М, —З—В–Њ –≥–ї–∞–≤–љ—Л–Љ –Њ–њ—А–∞–≤–і–∞–љ–Є–µ–Љ –≤–≤–µ–і–µ–љ–Є—П
–і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (8) –і–ї—П –®—А–µ–і–Є–љ–≥–µ—А–∞ —Б–ї—Г–ґ–Є—В —В–Њ,
—З—В–Њ –±–ї–∞–≥–Њ–і–∞—А—П —Н—В–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О —Г–і–∞–ї–Њ—Б—М –Є–Ј–±–∞–≤–Є—В—М—Б—П –Њ—В –Ј–∞–≥–∞–і–Њ—З–љ–Њ–≥–Њ
—В—А–µ–±–Њ–≤–∞–љ–Є—П —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ—Б—В–Є –≤ (1) –Є —В–µ–Љ —Б–∞–Љ—Л–Љ (–Њ–±–Љ–∞–љ—З–Є–≤–Њ
–ї–Њ–≥–Є—З–љ–Њ!) —Б–≤–µ—Б—В–Є –љ–µ–њ—А–Є–≤—Л—З–љ—Л–µ, –∞ –њ–Њ—В–Њ–Љ—Г –Ј–∞–≥–∞–і–Њ—З–љ—Л–µ, –Ј–∞–Ї–Њ–љ—Л –Љ–Є–Ї—А–Њ–Љ–Є—А–∞
–Ї –Є–Ј–≤–µ—Б—В–љ—Л–Љ —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –Ї–Њ–ї–µ–±–∞–љ–Є–є.
–Я–µ—А–≤–∞—П —А–∞–±–Њ—В–∞ –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ–Њ –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ –ї–µ–ґ–Є—В
–≤ —Б—В–Њ—А–Њ–љ–µ –Њ—В –Њ—Б–љ–Њ–≤–љ–Њ–≥–Њ –њ—Г—В–Є, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –≤ –і–∞–ї—М–љ–µ–є—И–µ–Љ —А–∞–Ј–≤–Є–≤–∞–ї–∞—Б—М
–і–∞–љ–љ–∞—П –≤–µ—В–≤—М –Ї–≤–∞–љ—В–Њ–≤–Њ–є —В–µ–Њ—А–Є–Є. –Э–µ —Б–Љ–Њ—В—А—П –љ–∞ —Н—В–Њ –Љ—Л –њ—А–Є–≤–µ–ї–Є
–њ–Њ–і—А–Њ–±–љ—Л–є –∞–љ–∞–ї–Є–Ј —А–∞–±–Њ—В—Л, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –љ–∞–Љ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В—Б—П
–≤–µ—Б—М–Љ–∞ –Є–љ—В–µ—А–µ—Б–љ—Л–Љ –њ—А–Њ—Б–ї–µ–і–Є—В—М —И–∞–≥ –Ј–∞ —И–∞–≥–Њ–Љ —Е–Њ–і –ґ–Є–≤–Њ–є
–Љ—Л—Б–ї–Є –≤–µ–ї–Є–Ї–Њ–≥–Њ –∞–≤—Б—В—А–Є–є—Б–Ї–Њ–≥–Њ —Д–Є–Ј–Є–Ї–∞ –Є —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ—А–Њ–љ–Є–Ї–љ—Г—В—М—Б—П –і—Г—Е–Њ–Љ
—Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –љ–∞—Г–Ї–Є - –љ–∞—Б—В–Њ—П—Й–Є–Љ –і—Г—Е–Њ–Љ –љ–µ–њ–Њ–і–і–µ–ї—М–љ–Њ–≥–Њ —В–≤–Њ—А—З–µ—Б—В–≤–∞ –Є
–≤–Њ–Ј–≤—Л—И–µ–љ–љ–Њ–≥–Њ –Є—Б–Ї–∞–љ–Є—П –Є—Б—В–Є–љ—Л, –Ї–Њ—В–Њ—А—Л–є –љ–∞—З–Є—Б—В–Њ –Є—Б—З–µ–Ј–∞–µ—В –≤ –ї–Њ–≥–Є—З–µ—Б–Ї–Њ–є
–≤—Л–≤–µ—А–µ–љ–љ–Њ—Б—В–Є –Є –Љ–µ—В–Њ–і–Є—З–µ—Б–Ї–Њ–є –њ—А–Є–ї–Є–Ј–∞–љ–љ–Њ—Б—В–Є —Б—В–∞–љ–і–∞—А—В–љ—Л—Е —Г—З–µ–±–љ—Л—Е –њ–Њ—Б–Њ–±–Є–є.
–Э–∞ —Н—В–Њ–Љ –Љ—Л –Ј–∞–≤–µ—А—И–∞–µ–Љ –њ–µ—А–≤—Г—О —З–∞—Б—В—М —Б—В–∞—В—М–Є, –њ–Њ—Б–≤—П—Й–µ–љ–љ–Њ–є 75-–ї–µ—В–Є—О
—Б–Њ–Ј–і–∞–љ–Є—П –≤–Њ–ї–љ–Њ–≤–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є. –°–ї–µ–і—Г—О—Й–Є–µ –і–≤–µ —З–∞—Б—В–Є –њ–ї–∞–љ–Є—А—Г–µ—В—Б—П –њ–Њ—Б–≤—П—В–Є—В—М
–Є–љ–Њ–Љ—Г "–≤—Л–≤–Њ–і—Г" —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –њ—А–Є –њ–Љ–Њ—Й–Є
–Њ–њ—В–Є–Ї–Њ-–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–є –∞–љ–∞–ї–Њ–≥–Є–Є –У–∞–Љ–Є–ї—М—В–љ–∞ –Є –ї–Њ–≥–Є–Ї–µ –љ–∞–њ–Є—Б–∞–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–Њ–Љ
–љ–µ—Б—В–∞—Ж–Є–љ–∞—А–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –і–ї—П —Н–≤–Њ–ї—О—Ж–Є–Є –≤–Њ–ї–љ–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є.


Copyright (c) "–†—Г—Б—Б–Ї–Є–є –њ–µ—А–µ–њ–ї–µ—В"








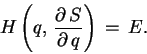
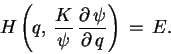
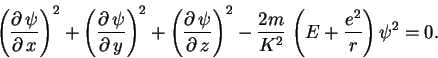
![\begin{displaymath}
\delta J =\delta\,\int\int\int\, dx\, dy\, dz\,
\left [
\lef...
...rac{2m}{K^2}\,\left (E+\frac{e^2}{r}\right )\psi^2
\right ]=0.
\end{displaymath}](img37.gif)
![\begin{displaymath}
\frac{1}{2}\,\delta J\,
=\,\int\, df\,\delta\psi\,\frac{\par...
...ac{2m}{K^2}\,\left (E+\frac{e^2}{r}\right )\,\psi
\right ] =0.
\end{displaymath}](img38.gif)
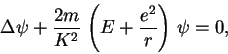
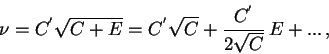
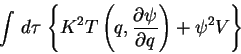
![\begin{displaymath} % latex2html id marker 406(\ref{ig})\,\Leftrightarrow\,\de...
...ight ]
\right )\,\psi +
\psi\, V(q)\,\psi
\right\}\, =\, 0,
\end{displaymath}](img58.gif)
