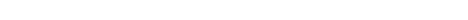п÷п╬я─я┌п╟п╩ | п║п╬п╢п╣я─п╤п╟п╫п╦п╣ | п· п╫п╟я│ | п░п╡я┌п╬я─п╟п╪ | п²п╬п╡п╬я│я┌п╦ | п÷п╣я─п╡п╟я▐ п╢п╣я│я▐я┌п╨п╟ | п■п╦я│п╨я┐я│я│п╦п╬п╫п╫я▀п╧ п╨п╩я┐п╠ | п╖п╟я┌ п²п╟я┐я┤п╫я▀п╧ я└п╬я─я┐п╪ п÷п╣я─п╡п╟я▐ п╢п╣я│я▐я┌п╨п╟ "п═я┐я│я│п╨п╬пЁп╬ п©п╣я─п╣п©п╩п╣я┌п╟" п╒п╣п╪я▀ п╢п╫я▐:

п°п╦я─ я│п╬п╠п╦я─п╟п╣я┌я│я▐ п╬п╠я┼я▐п╡п╦я┌я▄ п╠п╣я│п©п╬п╩я▒я┌п╫я┐я▌ п╥п╬п╫я┐ п╡ п╫п╟я┬п╣п╧ Vselennoy! | п÷я─п╣п╥п╦п╢п╣п╫я┌я┐ п÷я┐я┌п╦п╫я┐ п╬ я│п╬п╥п╢п╟п╫п╦п╦ п≤п╫я│я┌п╦я┌я┐я┌п╟ п≤я│я┌п╬я─п╦п╦ п═я┐я│я│п╨п╬пЁп╬ п²п╟я─п╬п╢п╟. |п²п╟я│ п©п╬я│п╣я┌п╦п╩п╬ 40 п╪п╩п╫. я┤п╣п╩п╬п╡п╣п╨ | п╖п╣п╪ п╥п╟п╫п╦п╪п╟п╩п╦я│я▄ я─я┐я│я│п╨п╦п╣ 4000 п╩п╣я┌ п╫п╟п╥п╟п╢? | п п╬п╪я┐ п╢п╟п╡п╟я┌я▄ пЁя─п╟п╫я┌я▀ п╦п╩п╦ я│п╨п╬п╩я▄п╨п╬ п╡ п═п╬я│я│п╦п╦ п╪п╬п╩п╬п╢я▀я┘ я┐я┤п╣п╫я▀я┘?

Celestial Mechanics 25 (1981) 33-40
 

Abstract. We present some results of new calculations of D" ( t )- the second derivative of the Moon's elongation as a function of time. The paper contains an explanation of the well-known R. Newton's effect -the rapid decline in D'' ( t ) from about 700 yr to about 1300 yr. The new graph of D''  is based on the revised dates of the ancient eclipses and has a qualitatively diffeient character; in particular, the decline in D'' ( t ) vanishes completely and D'' ( t ) oscillates at a roughly constant value, which coincides with the modern one. This fact agrees with the independent chronological results in the author's [7] paper.
 

1. It is important for some computational astronomical problems to know the behaviour of D'' -- the second derivative of the Moon's elongation - as a function of the time, on a rather long segment of the time line [1]. This problem, particularly, was talked about during the discussion organized in 1972 by the London Royal Society and British Academy of Sciences [1]. The scheme of the calculation of D''  is as follows: we are to fix the totality of ancient observations of eclipses, then calculate. on the basis of the modern theory, when these observations were made, and then compare the results of the calculations with the observed parameters to evaluate the Moon's acceleration ([4], [6]).

While calculating the date of an observation, the parameter D''  may be ignored. The dependence of D''  on t has been obtained by Newton ([4], [6]), who received 12 values (evaluations) for D'', based on 370 observations of ancient and medieval eclipses preserved in ancient documents ([4], p. 113). These eclipses were supplied with the dates contained in [2], [3]  [gorm].

Together with the results of Martin, who had investigated nearly 2000 telescope  observations of the Moon during 1627-1860, it was possible to construct an experimental graph of D'' ( t )  (Figure 1).

2. Newton: "The most striking feature of Figure 1 is the rapid decline in D'' from about 700 to about 1300 ... . This decline means (Newton, 1972b) that there was a 'square wave' in the osculating value of D''... . Such changes in D'', and such values, unexplainable by present geophysical theories ... , show that D'' has had surprisingly large values and that it has undergone large and sudden changes within the past 2000 yrs" ([4], p.114-115).

Paper [5] 'Astronomical Evidence Concerning Nongravitational Forces in the Earth-Moon System' is also devoted to attempts to explain this jump (break) of D'' up to order. Its summary is (according to [4], [5]): (1) In the V-VIth centuries there is a sharp downfall up to the order of the value of D'' (see Figure I): (2) values of D''  don't deviate far from zero till IV-Vth centuries: (3) values of D'' are close to the modern ones beginning from IX-Xth centuries: (4) during the V-Xth centuries there is an essential scattering of values of D''  with an amplitude of oscillations changing to 60"/century². (Here and elsewhere in the text the boundaries of time-intervals are approximate.)

3. In this paper some results of new calculations of D''  are presented, based on the specification of some astronomical observed data whose dates are necessary for the calculation of D''.

The graph of D'' I have constructed has a qualitatively different character, in particular the jump (break) up to an order vanishes completely and D'' oscillates at a roughly constant value, which coincides with the modern one.

4. Let X be a set of all preserved recordings of observations of ancient Sun and Moon eclipses (see the list in [2], pp. 167-271): let A be a set of eclipses described in X (any eclipse aÎA may have some records corresponding to it and form X(a)).

Let t(a) be a date of observation, which is given to 'a' according to tradition, and which is fixed in [2], [3]. The numbers {t(a), aÎA} form the basis of the calculation of D'' . To calculate D'' (t(a)) we have to compare calculated data, computed (according to the modern Moon's motion theory) along the interval (t (a), t'), where t'  is a modern date, with the data contained in X(a) ÌX. The result of this comparison depends on the choice of the date t(a). For the calculation of 'D', only those X(a) are important which contain fairly full information about the eclipse 'a'. The analysis of the whole list X(a) (see [2]) allows us to make a sublist X₀ = U_aÎAX₀(a₀), where the index '0' points to the eclipse and its descriptions of which relatively many data (of information) have been preserved. I omit the list X₀ because of lack of space
[gorm].

5. Newton's attempts to explain the jump of D'' were not concerned with the question of the exactitude of the dates t (a), attributed in [2], [3] to the eclipses a₀ÎA: i.e. how exactly the parameters of 'a₀' fixed in X₀(a₀) and the parameters of 'a₀' calculated according to the modern Moon's motion theory, correspond to each other. The recount of dates t(a₀), a₀ÎA, (-700) <t(a₀)<(+400), was first made by N. A. Morosov. The repeated series of checks was carried on by me, taking some new data into consideration. Let P(a₀) be a set of values of parameters of eclipse a₀ÎA₀ contained in X₀(a₀). In [2], [3] the whole list Vof all eclipses v, (-900) < t(v)< (+600), (+100) <t(v)<(+1582), calculated according to the theory, is given. In addition, for each vÎV a list S(v) of all the technical characteristics (t(v), the phase of v and so on) is given. The problem of calculating t(a₀) is solved as follows: we are to compare P(a₀) with all S(v), vÎV, and are to choose only those v', which have S(v') (or its part) coinciding with P(a₀). At the same time all parameters of P(a₀) are to coincide with the parameters of S(v'). The novelty of this method M is the fulfilment of the requirement: P(a₀) ÍS(v'), and the extension of the interval for the search of the solution S(v') to the interval (-900,  +1600).

6. The application of this method to A₀ divides it into two disjointed sets A₀^- and A₀⁺ where A₀^- = {a₀ | -900 < t(a₀)< +400}, A₀⁺ = {a₀ | +400 < t(a₀)< +1600}. Let t'(a₀) be a number given to 'a₀' by the method M. As a result the following inequality holds for most of a₀ÎA₀^- : t'(a₀) > t(a₀); moreover, t'(a₀) Î (+400, +1600), and we have t'(a₀) = t(a₀) Î (+400, +1600) for a₀ÎA₀⁺. (The exact list of A₀^-, A₀⁺ is omitted because of lack of space.) The difference between t'(a₀) and t(a₀) is explained, as was shown by working out A₀([2], [3]), by the fact that previous investigators admitted deviations (of different amplitude) of S(v') from P(a₀) when choosing S(v'). They were forced to do so because of the traditional restriction t(a₀) Î (-900, +400), established before [2] and [3] were published and earlier methods of astronomical dating.

7. The formal method M also removes the difficulties which occurred earlier, when dates t(a₀), a₀ÎA₀^- were proved astronomically. I shall only give one typical example. Three eclipses a₁, a₂, a₃ (see Nos. 6,8,9 in [2], pp. 176-179) are joined into a triad because they are described in the same X₀, i.e. X₀(a₁) = X₀(a₂) = X₀(a₃). The list P(a₁, a₂, a₃) gives, with a view to X₀, some of the following technical characteristics of the triade; (1) a₁, a₂, a₃ occurred in a square with the following approximate geographical coordinates: 15°< j< 30°; 30°< y < 42°, where (j is the value of latitude and y is the value of longitude; (2) a₁ is a Sun's eclipse; (3) a₂ is a Sun's eclipse; (4) a₃ is a Moon's eclipse; (5) the interval between a₁ and a₂ is equal to 7 yrs; (6) the interval between a₂ and a₃ is equal to 11 yrs; (7) a₁ occurs in summer; (8) a₁ is a full eclipse (stars are seen); (9) a₁ occurs in the afternoon (local time); (10) a₂ occurs at the beginning of the summer; (11) a₃ occurs at the end of the summer; (12) a₂ occurs in March. See Thucydides, 'History of Peloponnesian War'.

The condition of No. 12 is not clearly defined by X and is not included in P(a₁, a₂, a₃). The solution t(a₁)=-430, t(a₂)=-423, t(a₃) = -412 (Petavius and Kepler, see [2]) does not satisfy all the conditions of Nos. 1-11, because, for example, a₁ is not a full but a ring-like eclipse (and is not full anywhere) and has a phase of 10" (from the point of observation, see [2]). Cf. also Ginzel: "An der Kleinheit der Verfinsterungsphase haben einige Anstoss genommen ... bei der aus den neueren Rechnungen resultierenden Phase von 10"...' ([2]. p. 176).

Numerous publications have been devoted to the eclipse a₁ and its dating (see [2]. p. 176). Besides, the zone of a₁ passed the place of observation only at about 17.00 hrs local time, which implies a too extensive interpretation of the condition of No. 9. The calculation of the position of bright planets carried out earlier has shown that their coordinates do not provide their visibility (for example. Mars was only 3° over the horizon. Saturn was under the horizon and so on (see [2], p. 176).  [gorm] In spite of the fact that some conditions do not hold in the solution just described, this date t(a₁)=-430 was retained because there is no other, more suitable, dates in the interval (-600, -200) (see [2]). The application of method M and the extension of the solution interval to (-900. +1600) provides an answer: (1) there exist two triads fully satisfying all conditions: (2) they are unique in the interval ( -900, + 1600); (3) the solution is t'(a₁) = +1133(2/VIII); t'(a₂) = +1140(20/III); t'(a₃) = +1151(28/VIII). Condition No. 12 also holds. The second solution obtained by the author is: +1039(22/VIII), +1046(9/IV), +1151(15/IX).  [gorm]

We would also like to mention No. 27 as a typical example (see [2], pp. 190-191). Here t(a) = -167, (21/VI) (a Lunar eclipse), and again method M provides an answer: t'(a) = +415(5/IX) or +955(5/1X). The solution t(a) = -167 is not in accordance with the calendar information contained in No. 27 ([2]. pp. 190-191).  [gorm]

8. So, for a₀ÎA₀^- we have: t'(a₀) > t(a₀). As a result of working out the whole list X₀ we found a distinct border, separating dates t(a₀). which are confirmed by method M, from dates t(a₀)) which are replaced by more exact (transfer up) ones up to M. This border is about the IV-X centuries.
 

9. In the behaviour of D" calculated on the basis of the former dates t(a₀) there was a clear-cut border having a sharp downfall beginning in about the V century. These two borders (see point No. 8) coincide, and this fact can point to a connection between the jump of D" and the replacement of the dates t(a₀), a₀ÎA₀^- by t'(a₀).

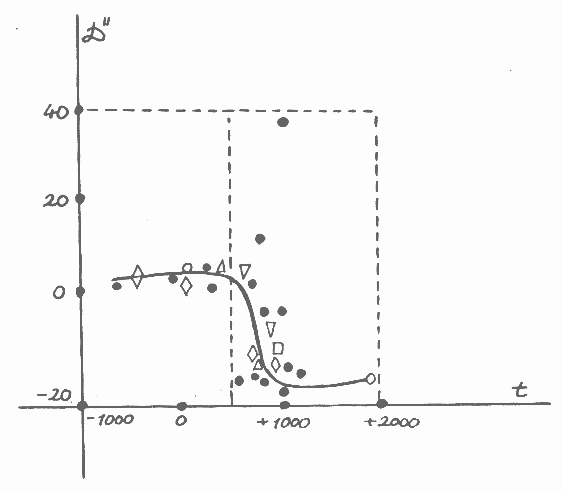
10. Let us set up a correspondence between each a₀ÎA₀ and the specified value t' (a₀) and then calculate D"(t' (a₀)), a₀ÎA₀^-. This graph will differ from the previous one (the procedure was carried out by me). This result is seen in Figure 2; it was found that the replacement of t(a₀) by t' (a₀)  (with a₀ÎA₀^-) not only transferred a₀ÎA₀^- up, but also identified it with many a'₀ÎA₀⁺ [gorm]. So it factorizes the list A₀, identifying a₀ and a'₀, with t'(a₀)=t (a'₀). This implies that we must add a new list of parameters P(a₀) to the previous list P(a'₀), i.e., while calculating D"(t(a'₀)) we are to consider P(a₀) in addition to P(a'₀) (see Figure 3).

It now turns out that the appearance of such additional lists P(a₀) (as a result of their redating for some a'₀ÎA₀⁺, t'(a₀)=t(a'₀)) does not change the previous values D"(t(a'₀)).

The conclusion is: the new graph of D" in the interval ( +400, +1600) coincides with the previous one, calculated only in accordance with P(a₀), t(a₀) > +400.

Let us note that by no means all a^*₀, t(a^*₀) > +400 are identified to any a₀ with t'(a₀)=t(a^*₀), t(a₀) < +400, up to this factorization.  [gorm]

11. The new graph of D" has a different domain from the previous one, since it is not defined for the interval ( -700, +400) because there is no number t'(a₀) < +400 (this fact was discovered after the whole list of eclipses had been investigated). During the IX-XXth centuries the parameter D" is practically constant and oscillates about ( -18"/(century)², i.e. these values of D" lie on the part of the former graph of D", calculated earlier on the interval IX-XX centuries only, on the basis of the lists P(a₀), t(a₀) > +400. The parameter D" had suffered no sharp change which is why we are not in all probability able to adduce any new geophysical nongravitational theory (see [5]). The scattering of values of D" increases with the motion to the left along the lime-line from + 1000 to 500, which apparently points to the inaccuracy of the observational information contained in P(a₀),   +400 < t(a₀) < +1000.

After this, but earlier than +400, there is a zone of absence of any observational data which could be used for the calculation of D". This reflects the natural picture of time distribution of observational data whose original precision was not high; but then it was increasing (with time), and this has brought about the gradual decrease in scattering of the set of values of D" with motion along the time-line from the left to the right.

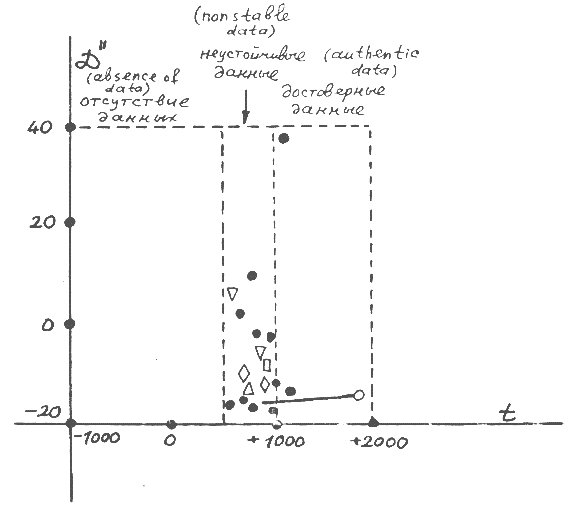
Comment to Figure 3. As we have seen, the dates of all ancient and early-medieval eclipses which received detailed description in documents are shifted in the period of the VIII-XV centuries. These displacements agree with the chronological graph in Figure 3 (discovered by the author in [7]). If the traditional date of an eclipse belongs to some time-interval marked for example as K on the line 'the chronology of Europe', then the new date of this eclipse belongs to one of the other time-intervals marked as K and placed to the right of the traditional date. It means that the new date of an eclipse differs from the traditional one by one of the following values: 333, 1053, 1778 (or 720 = 1053-333) years. In general, as was discovered in [7], the global chronology of Europe and that given in the Bible contain epochs which are duplicates. These duplicates are indicated in Figure 3 by the same symbols.

References

[1] 'The Place of Astronomy in the Ancient World', A discussion organized jointly for the Royal Society
and the British Academy. 1972, Phil. Trans. Roy. Soc. London. Ser. A, Math. and Phys. Sci. 276(1976), 1-276.
[2]. Ginzel, F. K.: 1899, Specieller Canon der Sonner und Mondfinsternisse, Berlin, Mayer-Muller.
[3] Oppolzer, Th.: 1887, Canon der Sonner und Mondfinsternisse, Denkschriften, Wien, 52.
[4] Newton, R. R. : 1974, 'Two Uses of Ancient Astronomy', Phil. Trans. Roy. Sic. London, Ser. A. Math. and Phys. Sci. 276,99-115.
[5] Newton. R. R. : 'Astronomical Evidence Concerning Non-gravitational Forces in the Earth-Moon
System', Astrophys. Space Sci. 16, 179-200.
[6] Newton, R. R.: 1970, 'Ancient Astronomical Observations and the Accelerations of the Earth and Moon', Baltimore, Md., Johns Hopkins Press.
[7] Fomenko, A. T. : 1980, 'Some Statistic Laws on Distribution of Information Density in Texts with a Scale', in Semiotics and Information 15,99-125. Moscow, VINITI. U.S.S.R.