[ ENGLISH ] [AUTO] [KOI-8R] [WINDOWS] [DOS]
[ISO-8859]
�


–Т.–Ы. –Я–∞–љ—В–µ–ї–µ–µ–≤

–Ґ–µ–Њ—А–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є
–Ы–µ–Ї—Ж–Є—П 1
–Я—А–µ–і–Љ–µ—В —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є
. вМ†–§–Є–≥—Г—А—ЛвЦ† –Є —Б—В—А–Њ–µ–љ–Є—П –њ–ї–∞–љ–µ—В. –У–µ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞. –Ю—Б–љ–Њ–≤–љ—Л–µ –њ–Њ–љ—П—В–Є—П —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –≥–µ–Њ–і–µ–Ј–Є–Є. –Ш—Б—В–Њ—А–Є—П –Є–Ј—Г—З–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є. –Ъ–Њ—Б–Љ–Є—З–µ—Б–Ї–∞—П –≥–µ–Њ–і–µ–Ј–Є—П.
–Ґ–µ–Њ—А–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є
–§–Є–≥—Г—А–∞ –њ–ї–∞–љ–µ—В—Л . . . —З—В–Њ —Н—В–Њ? –§–Њ—А–Љ–∞ –µвХ¶ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є? –§–Њ—А–Љ–∞ –Є–ї–Є —Д–Є–≥—Г—А–∞? –Т–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, —Н—В–Є –і–≤–∞ —Б–ї–Њ–≤–∞ –љ–µ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л, –µ—Б–ї–Є –Є—Е –њ—А–Є–Љ–µ–љ—П—В—М –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї –њ–ї–∞–љ–µ—В–µ. –Ґ–µ—А–Љ–Є–љ —Д–Є–≥—Г—А–∞ –Ч–µ–Љ–ї–Є –≤–≤–µ–івХ¶–љ –і–∞–≤–љ–Њ. –Ґ–∞–Ї —Г—З–µ–±–љ–Є–Ї –њ—А–Њ—Д. –Р.–Р.–Ь–Є—Е–∞–є–ї–Њ–≤–∞, –≤–њ–µ—А–≤—Л–µ –Є–Ј–і–∞–љ–љ—Л–є –≤ 1933 –≥–Њ–і—Г, –љ–∞–Ј—Л–≤–∞–µ—В—Б—П вМ†–Ъ—Г—А—Б –≥—А–∞–≤–Є–Љ–µ—В—А–Є–Є –Є —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–ЄвЦ†. –Ю–і–љ–∞–Ї–Њ –љ–µ –Њ–љ –≤–≤–µ–ї —Н—В–Њ—В —В–µ—А–Љ–Є–љ. –Т —В–Њ–Љ –ґ–µ –≥–Њ–і—Г –≤—Л—И–µ–ї –њ–µ—А–µ–≤–Њ–і –Ї–љ–Є–≥–Є –Я.–Я–Є—Ж–µ—В—В–Є вМ†–Ь–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–µ –Њ—Б–љ–Њ–≤—Л —Д–Є–≥—Г—А—Л –њ–ї–∞–љ–µ—ВвЦ†
. –Ю—А–Є–≥–Є–љ–∞–ї, –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ, –≤—Л—И–µ–ї —А–∞–љ—М—И–µ. –£ –Р.–Р.–Ь–Є—Е–∞–є–ї–Њ–≤–∞ –µ—Б—В—М —Б—Б—Л–ї–Ї–∞ –љ–∞ –Ї–љ–Є–≥—Г Buchholz H. Angewandte Mathematic. Das mechanische Potenzial und seine Anwendung zur Beschtimmung der Figur der Erde. Leipzig, 1916. –Ш–Љ–µ–µ—В—Б—П —Б—Б—Л–ї–Ї–∞ –Є –љ–∞ –±–Њ–ї–µ–µ —А–∞–љ–љ–Є–є –Є—Б—В–Њ—З–љ–Є–Ї: Todhunter J. A history of the mathematical Theory of Attraction and the Figure of the Earth. London, 1873. –Т —В–Њ–Љ –ґ–µ 1973 –≥–Њ–і—Г –љ–µ–Љ–µ—Ж–Ї–Є–є —Д–Є–Ј–Є–Ї –Ы–Є—Б—В–Є–љ–≥ –њ—А–µ–і–ї–Њ–ґ–Є–ї —В–µ—А–Љ–Є–љ –≥–µ–Њ–Є–і –і–ї—П –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В–µ—А–Љ–Є–љ —Д–Є–≥—Г—А–∞ –Ч–µ–Љ–ї–Є, –Ї–∞–Ї –њ—А–∞–≤–Є–ї–Њ, –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В —Д–Є–≥—Г—А—Г –µвХ¶ —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –њ—А–Є–љ—П—В–Њ–є –≤ –Ї–∞—З–µ—Б—В–≤–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Ї–Њ—В–Њ—А–Њ–є –Є–Ј–Љ–µ—А—П—О—В—Б—П –≤—Л—Б–Њ—В—Л –µвХ¶ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є.
–Я–Њ–і —Д–Є–≥—Г—А–Њ–є –њ–ї–∞–љ–µ—В—Л –Љ–Њ–ґ–љ–Њ –њ–Њ–љ–Є–Љ–∞—В—М:
- –§–Є–≥—Г—А—Г –µвХ¶ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є (–≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П —Д–Є–≥—Г—А–∞)
- –§–Є–≥—Г—А—Г —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є (–≥–µ–Њ–Є–і, —Б–µ–ї–µ–љ–Њ–Є–і, –∞—А–µ–Њ–Є–і –Є —В.–њ.)
- –Ф–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О —Д–Є–≥—Г—А—Г –њ–ї–∞–љ–µ—В—Л, –Ї–Њ—В–Њ—А–Њ–є —П–≤–ї—П–µ—В—Б—П —Ж–µ–љ—В—А–∞–ї—М–љ—Л–є —Н–ї–ї–Є–њ—Б–Њ–Є–і –Є–љ–µ—А—Ж–Є–Є.
–Ю—Б–Њ–±—Л–є –Є–љ—В–µ—А–µ—Б –≤—Л–Ј—Л–≤–∞—О—В —Д–Є–≥—Г—А—Л –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —В–µ–ї. –Х—Б–ї–Є –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Љ–Њ–і–µ–ї—М –њ–ї–∞–љ–µ—В—Л, —Б–Њ—Б—В–Њ—П—Й–µ–є –Є–Ј –Ї–Њ–љ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–Є—Е, —В–Њ–љ–Ї–Є—Е —Б–ї–ЊвХ¶–≤, –Є–Љ–µ—О—Й–Є—Е –љ–µ–Ї–Њ—В–Њ—А–Њ–µ —Б–ґ–∞—В–Є–µ, —В–Њ –і–ї—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —В–µ–ї –і–∞–≤–ї–µ–љ–Є–µ –≤–љ—Г—В—А–Є –Ї–∞–ґ–і–Њ–≥–Њ —Б–ї–Њ—П вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–Њ. –Ю—В—Б—Г—В—Б—В–≤—Г—О—В –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–µ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ —Б–Є–ї –і–∞–≤–ї–µ–љ–Є—П, —Б–њ–Њ—Б–Њ–±–љ—Л–µ —Б–Њ–Ј–і–∞—В—М —В–µ—З–µ–љ–Є—П. –Т–µ—А—В–Є–Ї–∞–ї—М–љ–∞—П —Б–Њ—Б—В–∞–≤–ї—П—О—Й–∞—П –і–∞–≤–ї–µ–љ–Є—П, –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–љ–∞—П —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В—М—О –≤–љ–µ—И–љ–Є—Е (–њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —В–Њ—З–Ї–µ) —Б–ї–ЊвХ¶–≤, –Ї–Њ–Љ–њ–µ–љ—Б–Є—А—Г–µ—В—Б—П —А–µ–∞–Ї—Ж–Є–µ–є –њ–Њ–і—Б—В–Є–ї–∞—О—Й–Є—Е —Б–ї–ЊвХ¶–≤. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П —Г—Б–ї–Њ–≤–Є–µ
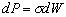 ,
,
–≥–і–µ
P вИЪ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –і–∞–≤–ї–µ–љ–Є—П, W вИЪ –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є, 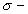 –њ–ї–Њ—В–љ–Њ—Б—В—М. –≠—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –і–ї—П –≤—Б–µ—Е —В–Њ—З–µ–Ї —В–µ–ї–∞ –њ–ї–∞–љ–µ—В—Л, –≤–Ї–ї—О—З–∞—П –µвХ¶ –≤–љ–µ—И–љ—О—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М. –Т –њ–Њ—Б–ї–µ–і–љ–µ–Љ —Б–ї—Г—З–∞–µ —Г—Б–ї–Њ–≤–Є–µ W = const –Њ–њ—А–µ–і–µ–ї—П–µ—В –Є —Д–Є–Ј–Є—З–µ—Б–Ї—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Љ–Њ–і–µ–ї–Є –њ–ї–∞–љ–µ—В—Л.
–њ–ї–Њ—В–љ–Њ—Б—В—М. –≠—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –і–ї—П –≤—Б–µ—Е —В–Њ—З–µ–Ї —В–µ–ї–∞ –њ–ї–∞–љ–µ—В—Л, –≤–Ї–ї—О—З–∞—П –µвХ¶ –≤–љ–µ—И–љ—О—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М. –Т –њ–Њ—Б–ї–µ–і–љ–µ–Љ —Б–ї—Г—З–∞–µ —Г—Б–ї–Њ–≤–Є–µ W = const –Њ–њ—А–µ–і–µ–ї—П–µ—В –Є —Д–Є–Ј–Є—З–µ—Б–Ї—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Љ–Њ–і–µ–ї–Є –њ–ї–∞–љ–µ—В—Л.
–Ч–∞–і–∞—З–∞ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ —Б—В—А–Њ–µ–љ–Є—П –њ–ї–∞–љ–µ—В—Л —З–∞—Б—В–Њ —Б–≤–Њ–і–Є—В—Б—П –Ї —Б–Њ–≥–ї–∞—Б–Њ–≤–∞–љ–Є—О –µвХ¶ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Є –љ–∞–±–ї—О–і–µ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є. –Я—А–Є —Н—В–Њ–Љ –µвХ¶ –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Њ–µ —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В—Б—П –Ї–∞–Ї –≥–Є–њ–Њ—В–µ–Ј–∞. –Ю—В—Б—О–і–∞ —П—Б–љ–Њ, —З—В–Њ —В–µ–Њ—А–Є—П —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –љ–µ–±–µ—Б–љ—Л—Е —В–µ–ї, —П–≤–ї—П—О—Й–∞—П—Б—П –Њ–і–љ–Є–Љ –Є–Ј –Ї—А—Г–њ–љ—Л—Е —А–∞–Ј–і–µ–ї–Њ–≤ –љ–µ–±–µ—Б–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є, –Є–Љ–µ–µ—В —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ.
–Ю—В–ї–Є—З–Є—П –Љ–Њ–і–µ–ї–Є –Њ—В –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–є —Д–Є–≥—Г—А—Л –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ —Г–Ї–∞–Ј—Л–≤–∞—О—В –љ–∞ –љ–µ–∞–і–µ–Ї–≤–∞—В–љ–Њ—Б—В—М –њ—А–Є–љ—П—В–Њ–є –Љ–Њ–і–µ–ї–Є —А–µ–∞–ї—М–љ–Њ–є –њ–ї–∞–љ–µ—В–µ. –≠—В–Є –Њ—В–ї–Є—З–Є—П –Љ–Њ–≥—Г—В –±—Л—В—М –Є –Є—Б—В–Њ—З–љ–Є–Ї–Њ–Љ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Є –Њ –≤–љ—Г—В—А–µ–љ–љ–Є—Е —Б–Є–ї–∞—Е, —Б–Њ–Ј–і–∞—О—Й–Є—Е –љ–∞–њ—А—П–ґ–µ–љ–Є—П —Б–і–≤–Є–≥–∞ –Є–ї–Є —А–∞—Б—В—П–ґ–µ–љ–Є—П. –Я—А–Є —В–µ–Ї—Г—З–µ—Б—В–Є –Љ–∞—В–µ—А–Є–∞–ї–∞ —Н—В–Є –љ–∞–њ—А—П–ґ–µ–љ–Є—П —Б–Њ–Ј–і–∞–і—Г—В –Ї–Њ–љ–≤–µ–Ї—Ж–Є–Њ–љ–љ—Л–µ —В–µ—З–µ–љ–Є—П, –Ї–Њ—В–Њ—А—Л–µ –љ–∞—Е–Њ–і—П—В –Њ—В—А–∞–ґ–µ–љ–Є–µ –≤ —В–µ–њ–ї–Њ–≤—Л—Е –Є –Љ–∞–≥–љ–Є—В–љ—Л—Е –њ–Њ–ї—П—Е –њ–ї–∞–љ–µ—В—Л. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Н—В–Є —П–≤–ї–µ–љ–Є—П –љ–µ –Љ–Њ–≥—Г—В –љ–µ –≤–ї–Є—П—В—М –љ–∞ –≤—А–∞—Й–µ–љ–Є–µ –њ–ї–∞–љ–µ—В—Л, –љ–∞ –і–≤–Є–ґ–µ–љ–Є–µ –Њ—В–і–µ–ї—М–љ—Л—Е –±–ї–Њ–Ї–Њ–≤ –µвХ¶ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Э–∞–±–ї—О–і–µ–љ–Є—П –Ј–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ–Љ —Д–Њ—А–Љ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –і–Њ—Б—В—Г–њ–љ—Л –≥–µ–Њ–і–µ–Ј–Є–Є –Є —П–≤–ї—П—О—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –≤–∞–ґ–љ–µ–є—И–Є—Е –њ—А–µ–і–Љ–µ—В–Њ–≤ –µвХ¶ –Є–Ј—Г—З–µ–љ–Є—П.
–Э–∞ —Б—В—Л–Ї–µ –љ–∞—Г–Ї вИЪ –≥–µ–Њ–і–µ–Ј–Є–Є, –≥–µ–Њ—Д–Є–Ј–Є–Ї–Є –Є –∞—Б—В—А–Њ–љ–Њ–Љ–Є–Є - –≤–Њ–Ј–љ–Є–Ї–ї–∞ –≥–µ–Њ–і–Є–љ–∞–Љ–Є–Ї–∞, –Њ–±—К–µ–і–Є–љ—П—О—Й–∞—П –Ї–Є–љ–µ–Љ–∞—В–Є—З–µ—Б–Ї—Г—О –Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї—Г—О –≥–µ–Њ–і–µ–Ј–Є–Є (—В–µ—А–Љ–Є–љ–Њ–ї–Њ–≥–Є—П –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ). –Т –њ–µ—А–≤–Њ–Љ —Б–ї—Г—З–∞–µ –Є–Ј—Г—З–∞—О—В –і–≤–Є–ґ–µ–љ–Є–µ, –≤–Њ –≤—В–Њ—А–Њ–Љ - —Б–Є–ї—Л. –°–µ–є—З–∞—Б –љ–∞—Г–Ї–Є –Њ –Ч–µ–Љ–ї–µ –Њ—З–µ–љ—М –Љ–љ–Њ–≥–Њ —Г–і–µ–ї—П—О—В –≤–љ–Є–Љ–∞–љ–Є—П –≥–µ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–Љ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П–Љ, –Ї–Њ—В–Њ—А—Л–µ –њ–Њ–Љ–Њ–≥–∞—О—В –њ—А–∞–≤–Є–ї—М–љ–Њ –Њ—Б–Љ—Л—Б–ї–Є—В—М –Љ–µ–і–ї–µ–љ–љ—Л–µ —Н–≤–Њ–ї—О—Ж–Є–Њ–љ–љ—Л–µ –њ—А–Њ—Ж–µ—Б—Б—Л, –њ—А–µ–і—Б–Ї–∞–Ј—Л–≤–∞—В—М –Ј–µ–Љ–ї–µ—В—А—П—Б–µ–љ–Є—П –Є –њ–Њ–і–і–µ—А–ґ–Є–≤–∞—В—М –≤—Л—Б–Њ–Ї—Г—О —В–Њ—З–љ–Њ—Б—В—М –∞—Б—В—А–Њ–љ–Њ–Љ–Њ-–≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є—Е —Б–µ—В–µ–є. –У–µ–Њ–і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є–µ –≤–∞—А–Є–∞—Ж–Є–Є –і–Њ—Б—В–Є–≥–∞—О—В –≤–µ–ї–Є—З–Є–љ
 –≤ –≥–Њ–і, —В–Њ –µ—Б—В—М 0,6-0,7 —Б–Љ —Б–Љ–µ—Й–µ–љ–Є—П, 1 вИЪ 10 –Љ–Ї–У–∞–ї –≤–∞—А–Є–∞—Ж–Є–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, 0,0002 вИЪ 0,02вМ† –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є.
–≤ –≥–Њ–і, —В–Њ –µ—Б—В—М 0,6-0,7 —Б–Љ —Б–Љ–µ—Й–µ–љ–Є—П, 1 вИЪ 10 –Љ–Ї–У–∞–ї –≤–∞—А–Є–∞—Ж–Є–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, 0,0002 вИЪ 0,02вМ† –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є.
–Т–µ—А–љвХ¶–Љ—Б—П –Ї —Д–Є–≥—Г—А–µ –Ч–µ–Љ–ї–Є. –†–µ–∞–ї—М–љ–∞—П —Д–Є–≥—Г—А–∞ –њ–ї–∞–љ–µ—В—Л, –µ—Б—В–µ—Б—В–≤–µ–љ–љ–Њ, –Њ—В–ї–Є—З–∞–µ—В—Б—П –Њ—В —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–Њ–є. –§–Є–Ј–Є—З–µ—Б–Ї–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Ч–µ–Љ–ї–Є, –і–∞ –Є –ї—О–±–Њ–є –њ–ї–∞–љ–µ—В—Л –љ–∞—Б—В–Њ–ї—М–Ї–Њ —Б–ї–Њ–ґ–љ–∞, —З—В–Њ –Њ–љ–∞ –љ–µ –њ–Њ–і–і–∞вХ¶—В—Б—П —Б—В—А–Њ–≥–Њ–Љ—Г –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–Љ—Г –Њ–њ–Є—Б–∞–љ–Є—О. –Э–∞–Є–±–Њ–ї–µ–µ –љ–∞–≥–ї—П–і–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ вИЪ –Ї–∞—А—В–∞ –≤—Л—Б–Њ—В —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞–і —Г—А–Њ–≤–љ–µ–Љ –Љ–Њ—А—П –Є–ї–Є –≥–µ–Њ–Є–і–∞ вИЪ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј –љ–∞—З–∞–ї–Њ –Њ—В—Б—ЗвХ¶—В–∞ –≤—Л—Б–Њ—В. –≠—В–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –±–ї–Є–Ј–Ї–∞ –Ї –љ–µ–≤–Њ–Ј–Љ—Г—ЙвХ¶–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≤–Њ–і–љ–Њ–є –≥–ї–∞–і–Є –Њ–Ї–µ–∞–љ–Њ–≤ –Є —Б–Њ–Њ–±—Й–∞—О—Й–Є—Е—Б—П —Б –љ–Є–Љ–Є –Љ–Њ—А–µ–є. –Ю–і–љ–∞–Ї–Њ, –Є–Ј-–Ј–∞ —А–∞–Ј–ї–Є—З–Є—П —В–µ–Љ–њ–µ—А–∞—В—Г—А—Л –Є —Б–Њ–ївХ¶–љ–Њ—Б—В–Є, –∞—В–Љ–Њ—Б—Д–µ—А–љ–Њ–≥–Њ –і–∞–≤–ї–µ–љ–Є—П –Є —В.–њ. –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –≤–Њ–і–љ–Њ–є –≥–ї–∞–і–Є –љ–µ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б—В—А–Њ–≥–Њ —Б –≥–µ–Њ–Є–і–Њ–Љ, –∞ –Њ—В–Ї–ї–Њ–љ—П–µ—В—Б—П –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ –≤ –њ—А–µ–і–µ–ї–∞—Е –Њ–і–љ–Њ–≥–Њ –Љ–µ—В—А–∞. –Э–∞–њ—А–Є–Љ–µ—А, –≤ –Ј–Њ–љ–µ –Я–∞–љ–∞–Љ—Б–Ї–Њ–≥–Њ –Ї–∞–љ–∞–ї–∞ —А–∞–Ј–љ–Њ—Б—В—М —Г—А–Њ–≤–љ–µ–є –Ґ–Є—Е–Њ–≥–Њ –Є –Р—В–ї–∞–љ—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–Ї–µ–∞–љ–Њ–≤ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 62 —Б–Љ
.
–Ф–ї—П –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –Ї–∞—А—В—Л –≤—Л—Б–Њ—В –љ—Г–ґ–љ–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П –Њ–Ї–µ–∞–љ–Њ–≤ –њ—А–Њ–і–Њ–ї–ґ–Є—В—М –њ–Њ–і –Ї–Њ–љ—В–Є–љ–µ–љ—В—Л. –°–і–µ–ї–∞—В—М —Н—В–Њ –љ–µ –њ—А–Њ—Б—В–Њ: –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –њ–ї–Њ—В–љ–Њ—Б—В–µ–є –≥–Њ—А–љ—Л—Е –њ–Њ—А–Њ–і. –≠—В–∞ —В—А—Г–і–љ–Њ—Б—В—М –±—Л–ї–∞ –њ—А–µ–Њ–і–Њ–ї–µ–љ–∞ –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–Љ: –≤–Љ–µ—Б—В–Њ –≥–µ–Њ–Є–і–∞ –Њ–љ –њ—А–µ–і–ї–Њ–ґ–Є–ї —Б—В—А–Њ–Є—В—М –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і, —З—В–Њ –љ–µ —В—А–µ–±—Г–µ—В –Ј–љ–∞–љ–Є—П –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ —Б—В—А–Њ–µ–љ–Є—П –Ј–µ–Љ–љ–Њ–є –Ї–Њ—А—Л.
–У–µ–Њ–і–µ–Ј–Є—П - –≤ –њ–µ—А–µ–≤–Њ–і–µ —Б –≥—А–µ—З–µ—Б–Ї–Њ–≥–Њ –Ј–µ–Љ–ї–µ—А–∞–Ј–і–µ–ї–µ–љ–Є–µ вИЪ —А–∞—Б–њ–Њ–ї–∞–≥–∞–µ—В –њ—А–Є–±–Њ—А–∞–Љ–Є –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Г–≥–ї–Њ–≤ –Є —А–∞—Б—Б—В–Њ—П–љ–Є–є, —В–Њ –µ—Б—В—М –Є–Љ–µ–µ—В –і–µ–ї–Њ —Б –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є. –Ю–і–љ–∞–Ї–Њ –і–ї—П –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–∞ —В—А–µ–±—Г–µ—В—Б—П –Ј–љ–∞—В—М –Є —Г–і–µ–ї—М–љ—Г—О —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є, —В–Њ –µ—Б—В—М –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–µ –њ–Њ–ї–µ. –Я–Њ—Н—В–Њ–Љ—Г —Н—В–Њ—В —А–∞–Ј–і–µ–ї –≥–µ–Њ–і–µ–Ј–Є–Є –љ–∞–Ј—Л–≤–∞—О—В —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –≥–µ–Њ–і–µ–Ј–Є–µ–є. –Ч–∞–і–∞—З–µ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –≥–µ–Њ–і–µ–Ј–Є–Є —П–≤–ї—П–µ—В—Б—П –љ–µ —В–Њ–ї—М–Ї–Њ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ —Д–Є–≥—Г—А—Л –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –њ–ї–∞–љ–µ—В—Л –Є–ї–Є –µвХ¶ –≥–µ–Њ–Є–і–∞ (—Б–µ–ї–µ–љ–Њ–Є–і–∞, –∞—А–µ–Њ–Є–і–∞ –Є —В.–њ.), –љ–Њ –Є –Є–Ј—Г—З–µ–љ–Є–µ –≥–µ–Њ–Љ–µ—В—А–Є–Є —Б–Є–ї–Њ–≤—Л—Е –ї–Є–љ–Є–є –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–∞, —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Є –µ–≥–Њ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—П —Б –і—А—Г–≥–Є–Љ–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–Љ–Є –њ–Њ–ї—П–Љ–Є. –Ґ–µ—А–Љ–Є–љ —Д–Є–Ј–Є—З–µ—Б–Ї–∞—П –≥–µ–Њ–і–µ–Ј–Є—П, –њ–Њ–ґ–∞–ї—Г–є, –Љ–Њ–ґ–љ–Њ –Њ—В–Њ–ґ–і–µ—Б—В–≤–Є—В—М —Б —В–µ—А–Љ–Є–љ–Њ–Љ —В–µ–Њ—А–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є, –µ—Б–ї–Є —Н—В–Њ—В –њ—А–µ–і–Љ–µ—В –њ–Њ–љ–Є–Љ–∞—В—М –±–Њ–ї–µ–µ —И–Є—А–Њ–Ї–Њ, —З–µ–Љ —Г–Ї–∞–Ј–∞–љ–Њ –≤ –µ–≥–Њ –љ–∞–Ј–≤–∞–љ–Є–Є.
–Ъ—А–∞—В–Ї–Є–є –Є—Б—В–Њ—А–Є—З–µ—Б–Ї–Є–є –Њ–±–Ј–Њ—А
–І—В–Њ —В–∞–Ї–Њ–µ –љ–∞—И–∞ –Ч–µ–Љ–ї—П? –Ъ–∞–Ї–Њ–є –Њ–љ–∞ —Д–Њ—А–Љ—Л? –≠—В–Є–Љ–Є –≤–Њ–њ—А–Њ—Б–∞–Љ–Є –Є–љ—В–µ—А–µ—Б–Њ–≤–∞–ї–Є—Б—М –љ–∞ —Б–∞–Љ–Њ–є –Ј–∞—А–µ –њ—А–Њ–±—Г–ґ–і–µ–љ–Є—П —Б–Њ–Ј–љ–∞–љ–Є—П. –Ф–Њ –љ–∞—Б –і–Њ—И–ї–Є —Б–≤–µ–і–µ–љ–Є—П, —З—В–Њ –Я–Є—Д–∞–≥–Њ—А, –ґ–Є–≤—И–Є–є –≤
V1 –≤–µ–Ї–µ –і–Њ –љ–∞—И–µ–є —Н—А—Л, —Б—З–Є—В–∞–ї –Ч–µ–Љ–ї—О —И–∞—А–Њ–Љ. –Х–≥–Њ –њ–Њ—З–µ–Љ—Г-—В–Њ –љ–µ —Б–Љ—Г—Й–∞–ї –≤–Њ–њ—А–Њ—Б, –Ї–∞–Ї –ґ–µ —Г–і–µ—А–ґ–Є–≤–∞—О—В—Б—П –≤—Б–µ –њ—А–µ–і–Љ–µ—В—Л –љ–∞ вМ†–њ–Њ–Ї–∞—В–Њ–євЦ† –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —И–∞—А–∞. –Ф–≤–∞ –≤–µ–Ї–∞ —Б–њ—Г—Б—В—П –≤–µ–ї–Є–Ї–Є–є –Р—А–Є—Б—В–Њ—В–µ–ї—М –њ—А—П–Љ–Њ —Г–Ї–∞–Ј–∞–ї –љ–∞ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ —И–∞—А–Њ–Њ–±—А–∞–Ј–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є. –≠—В–Њ вИЪ –ї—Г–љ–љ—Л–µ –Ј–∞—В–Љ–µ–љ–Є—П. –Ч–µ–Љ–ї—П –±—А–Њ—Б–∞–µ—В —В–µ–љ—М –љ–∞ –Ы—Г–љ—Г, –Ї–Њ–≥–і–∞ –°–Њ–ї–љ—Ж–µ –љ–∞—Е–Њ–і–Є—В—Б—П —Б –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Њ–є —Б—В–Њ—А–Њ–љ—Л. –Р —Н—В–∞ —В–µ–љ—М - –Ї—А—Г–≥–ї–∞—П! –Х—ЙвХ¶ –Њ–і–Є–љ –≥—А–µ—З–µ—Б–Ї–Є–є —Г—ЗвХ¶–љ—Л–є –≠—А–∞—В–Њ—Б—Д–µ–љ, –ґ–Є–≤—И–Є–є –≤ —В—А–µ—В—М–µ–Љ –≤–µ–Ї–µ –і–Њ –љ–∞—И–µ–є —Н—А—Л, –њ—А–µ–і–њ—А–Є–љ—П–ї –њ–µ—А–≤—Г—О –њ–Њ–њ—Л—В–Ї—Г –Њ–њ—А–µ–і–µ–ї–Є—В—М —А–∞–і–Є—Г—Б –Ч–µ–Љ–љ–Њ–≥–Њ —И–∞—А–∞. –Ю–љ –Њ—Ж–µ–љ–Є–ї –і–ї–Є–љ—Г –і—Г–≥–Є –Љ–µ—А–Є–і–Є–∞–љ–∞ –Љ–µ–ґ–і—Г –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–µ–є –Є –Р—Б—Б—Г–∞–љ–Њ–Љ (–°–Є–µ–љ–Њ–є) –Є –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї—Б—П —В–µ–Љ, –≤ –і–µ–љ—М –ї–µ—В–љ–µ–≥–Њ —Б–Њ–ї–љ—Ж–µ—Б—В–Њ—П–љ–Є—П –°–Њ–ї–љ—Ж–µ –≤ –Р—Б—Б—Г–∞–љ–µ —Б—В–Њ–Є—В —В–Њ—З–љ–Њ –≤ –Ј–µ–љ–Є—В–µ. –Ю–љ–Њ –Љ–Њ–ґ–µ—В вМ†–Ј–∞–≥–ї—П–љ—Г—В—МвЦ† –і–∞–ґ–µ –≤ —Б–∞–Љ—Л–µ –≥–ї—Г–±–Њ–Ї–Є–µ –Ї–Њ–ї–Њ–і—Ж—Л. –Т —Н—В–Њ –ґ–µ –≤—А–µ–Љ—П –≤ –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–Є –љ–∞–Є–Љ–µ–љ—М—И–µ–µ –Ј–µ–љ–Є—В–љ–Њ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –°–Њ–ї–љ—Ж–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 1/50 –і–Њ–ї—О –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Ь–µ–ґ–і—Г –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–µ–є –Є –Р—Б—Б—Г–∞–љ–Њ–Љ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї –Ї–∞—А–∞–≤–∞–љ–љ—Л–є –њ—Г—В—М –і–ї–Є–љ–Њ–є –≤ 5000 —Б—В–∞–і–Є–є, —В–Њ –µ—Б—В—М –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ 800- 900 –Ї–Љ. –Ґ–Њ—З–љ–∞—П –і–ї–Є–љ–∞ —Б—В–∞–і–Є–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ–∞, –њ–Њ–ї–∞–≥–∞—О—В, —З—В–Њ –Њ–љ–∞ —А–∞–≤–љ–∞ 0,158 вИЪ 0,185 –Ї–Љ. –£–Љ–љ–Њ–ґ–∞—П 5000 –љ–∞ 50, –≠—А–∞—В–Њ—Б—Д–µ–љ –њ–Њ–ї—Г—З–Є–ї –і–ї–Є–љ—Г –Љ–µ—А–Є–і–Є–∞–љ–∞, —А–∞–≤–љ—Г—О 250000 —Б—В–∞–і–Є–є. –†–∞–і–Є—Г—Б –Ч–µ–Љ–ї–Є, –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ, –±—Г–і–µ—В —А–∞–≤–µ–љ 40000 —Б—В–∞–і–Є–є, —В–Њ –µ—Б—В—М 6000 - 7400 –Ї–Љ. –°–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б—А–µ–і–љ–µ–≥–Њ —А–∞–і–Є—Г—Б–∞ –Ч–µ–Љ–ї–Є —А–∞–≤–љ–Њ 6371.023 –Ї–Љ. –Ґ–∞–Ї —З—В–Њ —А–µ–Ј—Г–ї—М—В–∞—В –≠—А–∞—В–Њ—Б—Д–µ–љ–∞ –љ–µ–њ–ї–Њ—Е–Њ–є.
–Я–µ—А–≤—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П —А–∞–Ј–Љ–µ—А–Њ–≤ –Ч–µ–Љ–ї–Є –±—Л–ї–Є –Њ—Б–љ–Њ–≤–∞–љ—Л –љ–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–Є –і–ї–Є–љ –і—Г–≥. –Т–њ–Њ—Б–ї–µ–і—Б—В–≤–Є–Є —Н—В–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є —А–∞–Ј–≤–Є–ї–Њ—Б—М –Ї–∞–Ї –≥—А–∞–і—Г—Б–љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Т V11 –≤–µ–Ї–µ –≤ –њ–µ—А–Є–Њ–і —А–∞—Б—Ж–≤–µ—В–∞ –∞—А–∞–±—Б–Ї–Њ–є —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є–Є –±—Л–ї–Є –≤—Л–њ–Њ–ї–љ–µ–љ—Л –≥—А–∞–і—Г—Б–љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П , –њ—А–Є—З–µ–Љ –њ—А–Њ–≤–Њ–і–Є–ї–Є—Б—М –Є —Г–≥–ї–Њ–≤—Л–µ –Є –ї–Є–љ–µ–є–љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П. –£–≥–ї–Њ–≤—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Њ–љ–Є –≤—Л–њ–Њ–ї–љ—П–ї–Є –њ–Њ –љ–∞–±–ї—О–і–µ–љ–Є—П–Љ –≤—Л—Б–Њ—В –Ј–≤вХ¶–Ј–і –≤ –Љ–µ—А–Є–і–Є–∞–љ–µ. –£ –љ–Є—Е –Њ–і–Є–љ –≥—А–∞–і—Г—Б –Њ–Ї–∞–Ј–∞–ї—Б—П —А–∞–≤–љ—Л–Љ 111.8 –Ї–Љ, –∞ —А–∞–і–Є—Г—Б –Ч–µ–Љ–ї–Є - 6406 –Ї–Љ вИЪ –њ–Њ—З—В–Є —Б–Њ–≤—А–µ–Љ–µ–љ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В
–Ч–∞—В–µ–Љ —Б–љ–Њ–≤–∞ –љ–∞—Б—В—Г–њ–Є–ї –њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ—Л–є –њ–µ—А–µ—А—Л–≤. –Ю–љ —Б–≤—П–Ј–∞–љ —Б –њ–∞–і–µ–љ–Є–µ–Љ –∞—А–∞–±—Б–Ї–Њ–є —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є–Є –њ–Њ–і –≤–ї–Є—П–љ–Є–µ–Љ —Н–Ї—Б–њ–∞–љ—Б–Є–Є –Љ–Њ–љ–≥–Њ–ї—М—Б–Ї–Є—Е –њ–ї–µ–ЉвХ¶–љ –Є —Б—А–µ–і–љ–µ–≤–µ–Ї–Њ–≤–Њ–є —Б—Е–Њ–ї–∞—Б—В–Є–Ї–Є, –Ї–Њ—В–Њ—А–∞—П –љ–∞–і–Њ–ї–≥–Њ –Ј–∞–і–µ—А–ґ–∞–ї–∞ —А–∞–Ј–≤–Є—В–Є–µ –љ–∞—Г—З–љ–Њ–є –Љ—Л—Б–ї–Є. –Ґ–Њ–ї—М–Ї–Њ –≤ XV –≤–µ–Ї–µ –≤ –Х–≤—А–Њ–њ–µ –њ–Њ—П–≤–Є–ї—Б—П –Є–љ—В–µ—А–µ—Б –Ї —А–∞–Ј–Љ–µ—А–∞–Љ –љ–∞—И–µ–є –њ–ї–∞–љ–µ—В—Л. –Ю–љ —Б–≤—П–Ј–∞–љ —Б —А–∞–Ј–≤–Є—В–Є–µ–Љ —В–Њ—А–≥–Њ–≤—Л—Е –Њ—В–љ–Њ—И–µ–љ–Є–є –Є –Ї–Њ–ї–Њ–љ–Є–Ј–∞—Ж–Є–µ–є –і–∞–ї—М–љ–Є—Е –Ј–µ–Љ–µ–ї—М. –Э–µ–Њ–±—Е–Њ–і–Є–Љ—Л –±—Л–ї–Є —В–Њ—З–љ—Л–µ –Љ–Њ—А—Б–Ї–Є–µ –Ї–∞—А—В—Л. –†–Њ–і–Є–ї–∞—Б—М –≥–µ–Њ–і–µ–Ј–Є—П. –У–Њ–ї–ї–∞–љ–і—Б–Ї–Є–є —Г—З–µ–љ—Л–є –°–љ–µ–ї–ї–Є—Г—Б (1580-1626) –њ—А–µ–і–ї–Њ–ґ–Є–ї –Љ–µ—В–Њ–і —В—А–Є–∞–љ–≥—Г–ї—П—Ж–Є–Є. –Ю—Б–љ–Њ–≤–љ–∞—П –Є–і–µ—П –Љ–µ—В–Њ–і–∞ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ–±—Л —Б –њ–Њ–Љ–Њ—Й—М—О –Є–Ј–Љ–µ—А–µ–љ–Є—П —В–Њ–ї—М–Ї–Њ –Њ–і–љ–Њ–≥–Њ –±–∞–Ј–Є—Б–љ–Њ–≥–Њ –Њ—В—А–µ–Ј–Ї–∞ –Є –Є–Ј–Љ–µ—А–µ–љ–Є—П —Г–≥–ї–Њ–≤ –њ–Њ–ї—Г—З–Є—В—М —А–∞—Б—Б—В–Њ—П–љ–Є–µ –і–Њ –ї—О–±–Њ–є –і—А—Г–≥–Њ–є —В–Њ—З–Ї–Є, –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –≤–љ–µ –±–∞–Ј–Є—Б–∞. –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г —В–Њ—З–Ї–∞–Љ–Є –Р –Є –Т –Є–Ј–Љ–µ—А—П–µ—В—Б—П —Б –љ–∞–Є–±–Њ–ї—М—И–µ–є –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ–є —В–Њ—З–љ–Њ—Б—В—М—О (—А–Є—Б.1). –Ш–Ј–Љ–µ—А—П—П —Г–≥–ї—Л 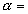 Ð
BAC –Є
Ð
BAC –Є 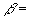 Ð
BAC, –±—Г–і–µ–Љ –Є–Љ–µ—В—М –≤—Б–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–°, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –±—Г–і–µ–Љ –Ј–љ–∞—В—М —Б—В–Њ—А–Њ–љ—Г –Т–°. –ХвХ¶ –Љ—Л –Љ–Њ–ґ–µ–Љ —Б—З–Є—В–∞—В—М –±–∞–Ј–Є—Б–Њ–Љ –і–ї—П —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BCD. –Я–Њ–≤—В–Њ—А—П—П –Њ–њ–µ—А–∞—Ж–Є–Є —Б –Є–Ј–Љ–µ—А–µ–љ–Є–µ–Љ —Г–≥–ї–Њ–≤, –Њ–њ—А–µ–і–µ–ї–Є–Љ —Б—В–Њ—А–Њ–љ—Л –љ–Њ–≤–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –¶–µ–њ–Њ—З–Ї–∞, —Б–Њ—Б—В–Њ—П—Й–∞—П –Є–Ј —В–∞–Ї–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –Љ–Њ–ґ–µ—В –±—Л—В—М –Ї–∞–Ї —Г–≥–Њ–і–љ–Њ –і–ї–Є–љ–љ–Њ–є. –Ю—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–µ–Ї, —З—В–Њ–±—Л —А–∞–Ј–≤–µ—А–љ—Г—В—М –і–∞–љ–љ—Г—О —В—А–Є–∞–љ–≥—Г–ї—П—Ж–Є–Њ–љ–љ—Г—О —Б–µ—В—М –љ–∞ —Б—Д–µ—А–µ –Є–ї–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –≠—В–Њ—В –Љ–µ—В–Њ–і –Њ–Ї–∞–Ј–∞–ї—Б—П –Њ—З–µ–љ—М —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л–Љ –Є –і–Њ–ґ–Є–ї –і–Њ –љ–∞—Б—В–Њ—П—Й–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є.
Ð
BAC, –±—Г–і–µ–Љ –Є–Љ–µ—В—М –≤—Б–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ —Б–≤–µ–і–µ–љ–Є—П –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–°, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –±—Г–і–µ–Љ –Ј–љ–∞—В—М —Б—В–Њ—А–Њ–љ—Г –Т–°. –ХвХ¶ –Љ—Л –Љ–Њ–ґ–µ–Љ —Б—З–Є—В–∞—В—М –±–∞–Ј–Є—Б–Њ–Љ –і–ї—П —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BCD. –Я–Њ–≤—В–Њ—А—П—П –Њ–њ–µ—А–∞—Ж–Є–Є —Б –Є–Ј–Љ–µ—А–µ–љ–Є–µ–Љ —Г–≥–ї–Њ–≤, –Њ–њ—А–µ–і–µ–ї–Є–Љ —Б—В–Њ—А–Њ–љ—Л –љ–Њ–≤–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –¶–µ–њ–Њ—З–Ї–∞, —Б–Њ—Б—В–Њ—П—Й–∞—П –Є–Ј —В–∞–Ї–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤, –Љ–Њ–ґ–µ—В –±—Л—В—М –Ї–∞–Ї —Г–≥–Њ–і–љ–Њ –і–ї–Є–љ–љ–Њ–є. –Ю—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–µ–Ї, —З—В–Њ–±—Л —А–∞–Ј–≤–µ—А–љ—Г—В—М –і–∞–љ–љ—Г—О —В—А–Є–∞–љ–≥—Г–ї—П—Ж–Є–Њ–љ–љ—Г—О —Б–µ—В—М –љ–∞ —Б—Д–µ—А–µ –Є–ї–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –≠—В–Њ—В –Љ–µ—В–Њ–і –Њ–Ї–∞–Ј–∞–ї—Б—П –Њ—З–µ–љ—М —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л–Љ –Є –і–Њ–ґ–Є–ї –і–Њ –љ–∞—Б—В–Њ—П—Й–µ–≥–Њ –≤—А–µ–Љ–µ–љ–Є.
–Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ –≥—А–∞–і—Г—Б–љ—Л–Љ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ —Б–ї–µ–і—Г–µ—В —Б—З–Є—В–∞—В—М —А–∞–±–Њ—В—Г –Я–Є–Ї–∞—А–∞ (–§—А–∞–љ—Ж–Є—П, 1620-1682). –С—Л–ї–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –і–ї–Є–љ–∞ –і—Г–≥–Є –Њ—В –Я–∞—А–Є–ґ–∞ –і–Њ –Р–Љ—М–µ–љ–∞, –Ї–Њ—В–Њ—А–∞—П –Њ–Ї–∞–Ј–∞–ї–∞—Б—М —А–∞–≤–љ–Њ–є 153689 –Љ , –∞ –≤ –≥—А–∞–і—Г—Б–љ–Њ–є –Љ–µ—А–µ - 1°
23¢
55²
. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–ї–Є–љ–∞ –Њ–і–љ–Њ–≥–Њ –≥—А–∞–і—Г—Б–∞ —Б–Њ—Б—В–∞–≤–Є–ї–∞ 111212 –Љ. –°–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –і–ї–Є–љ—Л –і—Г–≥–Є –Њ–і–љ–Њ–≥–Њ –≥—А–∞–і—Г—Б–∞ –љ–∞ —И–Є—А–Њ—В–µ –Я–∞—А–Є–ґ–∞ —А–∞–≤–љ–Њ 111221 –Љ, —В–Њ –µ—Б—В—М –Є–Ј–Љ–µ—А–µ–љ–Є—П –Я–Є–Ї–∞—А–∞ –Њ—В–ї–Є—З–∞—О—В—Б—П –≤—Б–µ–≥–Њ –љ–∞ 9 –Љ.
–Т
XV111 –≤–µ–Ї–µ –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Б—В–Њ–ї–Є—Ж–µ –Љ–Є—А–∞ вИЪ –Я–∞—А–Є–ґ–µ –≤–љ–Њ–≤—М –±—Л–ї–Є –Њ—А–≥–∞–љ–Є–Ј–Њ–≤–∞–љ—Л —Н–Ї—Б–њ–µ–і–Є—Ж–Є–Є. –Т —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ–Њ–є –Ј–Њ–љ–µ (–Я–µ—А—Г) —Н–Ї—Б–њ–µ–і–Є—Ж–Є—П –≤ —Б–Њ—Б—В–∞–≤–µ –С—Г–≥–µ, –У–Њ–і–µ–љ–∞ –Є –Ы–∞–Ї–Њ–љ–і–∞–Љ–Є–љ–∞ –Є–Ј–Љ–µ—А–Є–ї–∞ –і–ї–Є–љ—Г –і—Г–≥–Є –Љ–µ—А–Є–і–Є–∞–љ–∞ –Њ—В 0°
2вЦУ30вЦ† —Б–µ–≤–µ—А–љ–Њ–є —И–Є—А–Њ—В—Л –і–Њ 3°
4вЦУ30вЦ† —О–ґ–љ–Њ–є —И–Є—А–Њ—В—Л. –Ч–љ–∞—З–µ–љ–Є–µ –і–ї–Є–љ—Л –і—Г–≥–Є –Њ–і–љ–Њ–≥–Њ –≥—А–∞–і—Г—Б–∞ –њ–Њ–ї—Г—З–µ–љ–Њ —А–∞–≤–љ—Л–Љ 110604 –Љ. –Т –њ–Њ–ї—П—А–љ–Њ–є –Ј–Њ–љ–µ (–°–Ї–∞–љ–і–Є–љ–∞–≤–Є—П) —А–∞–±–Њ—В–∞–ї–∞ –і—А—Г–≥–∞—П —Н–Ї—Б–њ–µ–і–Є—Ж–Є—П ( –Ъ–ї–µ—А–Њ, –Ь–Њ–њ–µ—А—В—О–Є, –Ъ–∞–Љ—О–Ј, –¶–µ–ї—М—Б–Є–є). –Ф–ї–Є–љ–∞ –Њ–і–љ–Њ–≥—А–∞–і—Г—Б–љ–Њ–є –і—Г–≥–Є –љ–∞ —И–Є—А–Њ—В–µ 66°
–Њ–Ї–∞–Ј–∞–ї–∞—Б—М —А–∞–≤–љ–Њ–є 111917 –Љ. –Э–∞–Ї–Њ–љ–µ—Ж, –љ–µ—Б–Ї–Њ–ї—М–Ї–Є–Љ–Є –≥–Њ–і–∞–Љ–Є —А–∞–љ—М—И–µ –±—Л–ї–∞ –Є–Ј–Љ–µ—А–µ–љ–∞ –і–ї–Є–љ–∞ –Њ–і–љ–Њ–≥—А–∞–і—Г—Б–љ–Њ–є –і—Г–≥–Є –њ–Њ–і –Я–∞—А–Є–ґ–µ–Љ. –Ю–љ–∞ –Њ–Ї–∞–Ј–∞–ї–∞—Б—М —А–∞–≤–љ–Њ–є 111258 –Љ. –†–µ–Ј—Г–ї—М—В–∞—В—Л –≥—А–∞–і—Г—Б–љ—Л—Е –Є–Ј–Љ–µ—А–µ–љ–Є–є –≤ XV111 –≤–µ–Ї–µ –Љ–Њ–ґ–љ–Њ —Б–≤–µ—Б—В–Є –≤ —Б–ї–µ–і—Г—О—Й—Г—О —В–∞–±–ї–Є—Ж—Г
|
–®–Є—А–Њ—В–∞, –≥—А–∞–і—Г—Б—Л |
–Ф–ї–Є–љ–∞ –Њ–і–љ–Њ–≥—А–∞–і—Г—Б–љ–Њ–є –і—Г–≥–Є, –Љ–µ—В—А—Л |
|
1 |
110604 |
|
49 |
111258 |
|
66 |
111917 |
–Я–Њ —Н—В–Є–Љ –і–∞–љ–љ—Л–Љ –ї–µ–≥–Ї–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –Є –±–Њ–ї—М—И—Г—О –њ–Њ–ї—Г–Њ—Б—М –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є –µ–≥–Њ —Б–ґ–∞—В–Є–µ
.
–Э—М—О—В–Њ–љ –і–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –Ч–µ–Љ–ї—П –Є–Љ–µ–µ—В —Д–Њ—А–Љ—Г —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П —Б–Њ —Б–ґ–∞—В–Є–µ–Љ 1:230 (—Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ 1:298,25). –≠—В—Г –≤–µ–ї–Є—З–Є–љ—Г –Њ–љ –њ–Њ–ї—Г—З–Є–ї —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є, –њ—А–Є–љ–Є–Љ–∞—П –Ч–µ–Љ–ї—О –Ј–∞ –Њ–і–љ–Њ—А–Њ–і–љ—Л–є, –ґ–Є–і–Ї–Є–є —Н–ї–ї–Є–њ—Б–Њ–Є–і. –°–Њ–≤—А–µ–Љ–µ–љ–љ–Є–Ї –Э—М—О—В–Њ–љ–∞ –У—О–є–≥–µ–љ—Б –Њ–њ—А–µ–і–µ–ї–Є–ї —Б–ґ–∞—В–Є–µ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є–љ–∞—З–µ. –Ю–љ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є–ї, —З—В–Њ —Б–Є–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤—Б–µ–≥–і–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –Ї —Ж–µ–љ—В—А—Г –Љ–∞—Б—Б –Ч–µ–Љ–ї–Є, –∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–Њ—Б—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П —Б–Њ–Ј–і–∞вХ¶—В —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–∞—П —Б–Є–ї–∞, –Ї–Њ—В–Њ—А–∞—П –Њ—В–Ї–ї–Њ–љ—П–µ—В –Њ—В–≤–µ—Б–љ—Г—О –ї–Є–љ–Є—О. –Т—Л—З–Є—Б–ї–Є–≤ —Б–ґ–∞—В–Є–µ, –Њ–љ –њ–Њ–ї—Г—З–Є–ї –≤–µ–ї–Є—З–Є–љ—Г, —А–∞–≤–љ—Г—О 1:576, —В–Њ –µ—Б—В—М —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –Љ–µ–љ—М—И–µ. –†–∞—Б—Е–Њ–ґ–і–µ–љ–Є–µ —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –Э—М—О—В–Њ–љ–∞ –Є –У—О–є–≥–µ–љ—Б–∞ –њ–Њ–Ј–ґ–µ –Њ–±—К—П—Б–љ–Є–ї —Д—А–∞–љ—Ж—Г–Ј—Б–Ї–Є–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Ъ–ї–µ—А–Њ, –Ї–Њ—В–Њ—А—Л–є –њ–Њ–ї—Г—З–Є–ї —Д–Њ—А–Љ—Г–ї—Г –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Б–ґ–∞—В–Є—П –Њ—В –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ —Б—В—А–Њ–µ–љ–Є—П –њ–ї–∞–љ–µ—В—Л. –Ю–љ –Њ–±–Њ–±—Й–Є–ї —В–µ–Њ—А–Є—О —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –њ–ї–∞–љ–µ—В –Є –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ —Б–ї—Г—З–∞–Є –Э—М—О—В–Њ–љ–∞ –Є –У—О–є–≥–µ–љ—Б–∞ —П–≤–ї—П—О—В—Б—П —З–∞—Б—В–љ—Л–Љ–Є —Б–ї—Г—З–∞—П–Љ–Є –µ–≥–Њ –Љ–Њ–і–µ–ї–Є. –°–ґ–∞—В–Є–µ –њ–Њ –Ъ–ї–µ—А–Њ —А–∞–≤–љ–Њ
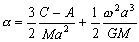
–Ф–ї—П –Њ–і–љ–Њ—А–Њ–і–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —Б –Љ–∞–ї—Л–Љ —Б–ґ–∞—В–Є–µ–Љ
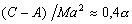 . –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Г—О –≤–µ–ї–Є—З–Є–љ—Г, –±–ї–Є–Ј–Ї—Г—О –Ї –Њ—В–љ–Њ—И–µ–љ–Є—О —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –Ї —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ —З–µ—А–µ–Ј q, –њ–Њ–ї—Г—З–Є–Љ
. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Г—О –≤–µ–ї–Є—З–Є–љ—Г, –±–ї–Є–Ј–Ї—Г—О –Ї –Њ—В–љ–Њ—И–µ–љ–Є—О —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –Ї —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ —З–µ—А–µ–Ј q, –њ–Њ–ї—Г—З–Є–Љ
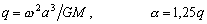 .
.
–Ф–ї—П –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –њ—А–Є–љ—П—В–Њ

–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, q = 0,003461407
–°–ґ–∞—В–Є–µ –њ–Њ –Э—М—О—В–Њ–љ—Г –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —А–∞–≤–љ–Њ
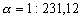 , –∞ –њ–Њ –У—О–є–≥–µ–љ—Б—Г
, –∞ –њ–Њ –У—О–є–≥–µ–љ—Б—Г 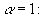 577.80. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –У–µ–љ–µ—А–∞–ї—М–љ–∞—П –Р—Б—Б–∞–Љ–±–ї–µ—П –Ь–Р–° –≤ 1976 –≥–Њ–і—Г —Г—В–≤–µ—А–і–Є–ї–∞ –Ј–љ–∞—З–µ–љ–Є–µ —Б–ґ–∞—В–Є—П –і–ї—П –Ч–µ–Љ–ї–Є
577.80. –Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –У–µ–љ–µ—А–∞–ї—М–љ–∞—П –Р—Б—Б–∞–Љ–±–ї–µ—П –Ь–Р–° –≤ 1976 –≥–Њ–і—Г —Г—В–≤–µ—А–і–Є–ї–∞ –Ј–љ–∞—З–µ–љ–Є–µ —Б–ґ–∞—В–Є—П –і–ї—П –Ч–µ–Љ–ї–Є 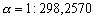 , –Ї–Њ—В–Њ—А–Њ–µ –ї–µ–ґ–Є—В –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –≤—Л—И–µ —Г–Ї–∞–Ј–∞–љ–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є. –≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –њ–ї–∞–љ–µ—В–∞ –Ч–µ–Љ–ї—П –љ–µ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Њ—А–Њ–і–љ—Л–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ –Є, –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ, –≤—Б—П –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–∞—П –Љ–∞—Б—Б–∞ –љ–µ —Б–Њ—Б—А–µ–і–Њ—В–Њ—З–µ–љ–∞ –≤ —Ж–µ–љ—В—А–∞ –њ–ї–∞–љ–µ—В—Л.
, –Ї–Њ—В–Њ—А–Њ–µ –ї–µ–ґ–Є—В –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –≤—Л—И–µ —Г–Ї–∞–Ј–∞–љ–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є. –≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –њ–ї–∞–љ–µ—В–∞ –Ч–µ–Љ–ї—П –љ–µ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Њ—А–Њ–і–љ—Л–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ –Є, –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ, –≤—Б—П –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–∞—П –Љ–∞—Б—Б–∞ –љ–µ —Б–Њ—Б—А–µ–і–Њ—В–Њ—З–µ–љ–∞ –≤ —Ж–µ–љ—В—А–∞ –њ–ї–∞–љ–µ—В—Л.
–Ш—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –Ъ–ї–µ—А–Њ –і–∞–ї–Є –љ–∞—З–∞–ї–Њ —Ж–µ–ї–Њ–є —Б–µ—А–Є–Є —А–∞–±–Њ—В —В–∞–Ї–Є—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–≤ –Ї–∞–Ї –Я—Г–∞–љ–Ї–∞—А–µ, –Ы–∞–њ–ї–∞—Б, –Ы–µ–ґ–∞–љ–і—А, –°—В–Њ–Ї—Б, –Т–Є—Е–µ—А—В, –Ф–∞—А–≤–Є–љ –Є –і—А. –Ю–љ–Є —Б–Њ–Ј–і–∞–ї–Є –љ–∞—Г—З–љ–Њ–µ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ, —В–µ—Б–љ–Њ –њ—А–Є–Љ—Л–Ї–∞—О—Й–µ–µ –Ї –љ–∞—И–µ–Љ—Г –њ—А–µ–і–Љ–µ—В—Г вИЪ —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –љ–µ–±–µ—Б–љ—Л—Е —В–µ–ї. –С–Њ–ї—М—И–Њ–є –≤–Ї–ї–∞–і –≤ —В–µ–Њ—А–Є—О —Д–Є–≥—Г—А –љ–µ–±–µ—Б–љ—Л—Е —В–µ–ї –≤–љ–µ—Б–ї–Є –Ь–∞–Ї–ї–Њ—А–µ–љ –Є –ѓ–Ї–Њ–±–Є, –Ї–Њ—В–Њ—А—Л–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї–Є —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В—М —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —В–µ–ї —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–Њ–є —Д–Њ—А–Љ—Л.
–Ф–ї—П –Є–Ј—Г—З–µ–љ–Є—П —Д–Њ—А–Љ—Л —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–є –і–µ—В–∞–ї—М–љ–Њ—Б—В—М—О –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤–≤–µ—Б—В–Є —В–µ–ї–Њ –Њ—В—Б—З–µ—В–∞, –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Ї–Њ—В–Њ—А–Њ–≥–Њ –Љ–Њ–ґ–љ–Њ –≤—Л—П–≤–Є—В—М —Н—В–Є –і–µ—В–∞–ї–Є. –Ф–ї—П –Ч–µ–Љ–ї–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ —В–µ–ї–∞ –Њ—В—Б—З–µ—В–∞ –±–µ—А—Г—В –Ј–µ–Љ–љ–Њ–є —Н–ї–ї–Є–њ—Б–Њ–Є–і. –Ґ–Њ–≥–і–∞ –Ј–∞–і–∞—З–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є —Б–≤–Њ–і–Є—В—Б—П –Ї –≤—Л—З–Є—Б–ї–µ–љ–Є—О –≤—Л—Б–Њ—В –≥–µ–Њ–Є–і–∞ –љ–∞–і —Н—В–Є–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ. –Ш—Б—Е–Њ–і–љ—Л–Љ –Љ–∞—В–µ—А–Є–∞–ї–Њ–Љ –і–ї—П —А–µ—И–µ–љ–Є—П —В–∞–Ї–Њ–є –Ј–∞–і–∞—З–Є —Б–ї—Г–ґ–∞—В –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ –Є –≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Б–≤–µ–і–µ–љ–Є—П, –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є.
–Т–њ–µ—А–≤—Л–µ –Ј–∞–і–∞—З—Г –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є –њ–Њ—Б—В–∞–≤–Є–ї –Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є —А–µ—И–Є–ї –°—В–Њ–Ї—Б. –Я—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–∞—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –њ–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–Љ—Г –њ–Њ–ї—О –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П —В–µ–Њ—А–µ–Љ–Њ–є –°—В–Њ–Ї—Б–∞
: –µ—Б–ї–Є —Г—А–Њ–≤–µ–љ–љ–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, —Ж–µ–ї–Є–Ї–Њ–Љ –Њ—Е–≤–∞—В—Л–≤–∞—О—Й–∞—П –Љ–∞—Б—Б—Л, –Є–Ј–≤–µ—Б—В–љ–∞, –Є–Ј–≤–µ—Б—В–љ—Л —В–∞–Ї–ґ–µ –Љ–∞—Б—Б–∞ –Є —Г–≥–ї–Њ–≤–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П, —В–Њ —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї –љ–∞ —Б–∞–Љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, —В–∞–Ї –Є –≤–Њ –≤—Б–µ–Љ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ.
–°–Є–Љ–≤–Њ–ї–Є—З–µ—Б–Ї–Є —Н—В–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї: 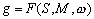 .–Э–∞—И–∞ –Ј–∞–і–∞—З–∞ вИЪ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є - —П–≤–ї—П–µ—В—Б—П –Њ–±—А–∞—В–љ–Њ–є: —В—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М S –њ–Њ –Ј–∞–і–∞–љ–љ—Л–Љ M, g –Є
.–Э–∞—И–∞ –Ј–∞–і–∞—З–∞ вИЪ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є - —П–≤–ї—П–µ—В—Б—П –Њ–±—А–∞—В–љ–Њ–є: —В—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М S –њ–Њ –Ј–∞–і–∞–љ–љ—Л–Љ M, g –Є  . –Ю—Б–љ–Њ–≤–љ–∞—П —В—А—Г–і–љ–Њ—Б—В—М —А–µ—И–µ–љ–Є—П —Н—В–Њ–є –Ј–∞–і–∞—З–Є —Б–≤—П–Ј–∞–љ–∞ —Б –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ g –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П. –Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ –Љ—Л –Љ–Њ–ґ–µ–Љ –Є–Ј–Љ–µ—А—П—В—М —Г–і–µ–ї—М–љ—Г—О —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є —В–Њ–ї—М–Ї–Њ –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Т–Њ–Ј–љ–Є–Ї–∞–µ—В –Ј–∞–і–∞—З–∞ –њ–µ—А–µ–љ–Њ—Б–∞ —Н—В–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П (—А–µ–і—Г–Ї—Ж–Є–Є) —Б —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ –≥–µ–Њ–Є–і (–љ–µ –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і!).
. –Ю—Б–љ–Њ–≤–љ–∞—П —В—А—Г–і–љ–Њ—Б—В—М —А–µ—И–µ–љ–Є—П —Н—В–Њ–є –Ј–∞–і–∞—З–Є —Б–≤—П–Ј–∞–љ–∞ —Б –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ g –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П. –Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ –Љ—Л –Љ–Њ–ґ–µ–Љ –Є–Ј–Љ–µ—А—П—В—М —Г–і–µ–ї—М–љ—Г—О —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є —В–Њ–ї—М–Ї–Њ –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Т–Њ–Ј–љ–Є–Ї–∞–µ—В –Ј–∞–і–∞—З–∞ –њ–µ—А–µ–љ–Њ—Б–∞ —Н—В–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П (—А–µ–і—Г–Ї—Ж–Є–Є) —Б —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ –≥–µ–Њ–Є–і (–љ–µ –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і!).
–Э–∞–і –њ—А–Њ–±–ї–µ–Љ–Њ–є —А–µ–і—Г–Ї—Ж–Є–Є —А–∞–±–Њ—В–∞–ї–Њ –Љ–љ–Њ–≥–Њ —Г—ЗвХ¶–љ—Л—Е. –Ф–Њ–Љ–Є–љ–Є—А—Г—О—Й—Г—О —А–Њ–ї—М –≤ —Н—В–Њ–є —В–µ–Њ—А–Є–Є —Б—Л–≥—А–∞–ї–Є –љ–∞—И–Є —Г—ЗвХ¶–љ—Л–µ. –Ю—Б–љ–Њ–≤–љ–∞—П —В—А—Г–і–љ–Њ—Б—В—М –Ј–∞–Ї–ї—О—З–∞–ї–∞—Б—М –≤ —В–Њ–Љ, –Ї–∞–Ї вМ†–Њ—В–њ—А–∞–≤–Є—В—МвЦ† –≤—Б–µ –Љ–∞—Б—Б—Л, –ї–µ–ґ–∞—Й–Є–µ –≤—Л—И–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≥–µ–Њ–Є–і–∞, –њ–Њ–і —Н—В—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –њ—А–Є —Н—В–Њ–Љ –љ–µ –Є—Б–Ї–∞–Ј–Є–≤ —Б–∞–Љ—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П. –≠—В–∞ –њ—А–Њ–±–ї–µ–Љ–∞ –њ–Њ–ї—Г—З–Є–ї–∞ –љ–∞–Ј–≤–∞–љ–Є–µ –њ—А–Њ–±–ї–µ–Љ—Л —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є –Ч–µ–Љ–ї–Є. –Я–Њ—Б–ї–µ–і–љ—О—О —В–Њ—З–Ї—Г –≤ —Н—В–Њ–є –Ј–∞–і–∞—З–µ –њ–Њ—Б—В–∞–≤–Є–ї –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є. –Ю–љ –і–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ —Д–Є–≥—Г—А—Г –Ч–µ–Љ–ї–Є –Љ–Њ–ґ–љ–Њ –Є–Ј—Г—З–∞—В—М –Є –±–µ–Ј —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є. –Ф–Њ—Б—В–∞—В–Њ—З–љ–Њ –≤—Б–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—Л–њ–Њ–ї–љ—П—В—М –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –љ–Њ –Ї—А–Њ–Љ–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М –Є –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –і–ї—П —З–µ–≥–Њ –і–Њ–ї–ґ–љ—Л –±—Л—В—М –≤—Л–њ–Њ–ї–љ–µ–љ—Л –Є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —А–∞–±–Њ—В—Л.
–Ш—В–∞–Ї, –њ—Г—Б—В—М –љ–∞ –Ј–µ–Љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–∞—Е —Б –Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є  –Є
–Є 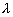 –±—Г–і–µ–Љ –Є–Љ–µ—В—М –≤–µ–Ї—В–Њ—А —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є g(j
l
) –Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї
–±—Г–і–µ–Љ –Є–Љ–µ—В—М –≤–µ–Ї—В–Њ—А —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є g(j
l
) –Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї  . –Ґ–Њ–≥–і–∞
. –Ґ–Њ–≥–і–∞ 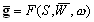 . –Ч–і–µ—Б—М —З–µ—А—В–∞ —Б–≤–µ—А—Е—Г –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –≤–µ–ї–Є—З–Є–љ—Л –±–µ—А—Г—В—Б—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S. –Х—Б–ї–Є S –Є W –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї—П—О—В –≤–µ–Ї—В–Њ—А g, —В–Њ —Г–Љ–µ—Б—В–љ–Њ –њ–Њ—Б—В–∞–≤–Є—В—М –Є –Њ–±—А–∞—В–љ—Г—О –Ј–∞–і–∞—З—Г: –Њ–њ—А–µ–і–µ–ї–Є—В—М S –њ–Њ –Ј–∞–і–∞–љ–љ—Л–Љ –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є g –Є W. –Я—А–Є —Н—В–Њ–Љ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –≤–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, –љ–µ —П–≤–ї—П–µ—В—Б—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П!
. –Ч–і–µ—Б—М —З–µ—А—В–∞ —Б–≤–µ—А—Е—Г –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –≤–µ–ї–Є—З–Є–љ—Л –±–µ—А—Г—В—Б—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S. –Х—Б–ї–Є S –Є W –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї—П—О—В –≤–µ–Ї—В–Њ—А g, —В–Њ —Г–Љ–µ—Б—В–љ–Њ –њ–Њ—Б—В–∞–≤–Є—В—М –Є –Њ–±—А–∞—В–љ—Г—О –Ј–∞–і–∞—З—Г: –Њ–њ—А–µ–і–µ–ї–Є—В—М S –њ–Њ –Ј–∞–і–∞–љ–љ—Л–Љ –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є g –Є W. –Я—А–Є —Н—В–Њ–Љ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –≤–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, –љ–µ —П–≤–ї—П–µ—В—Б—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П!
–Р–≤—Б—В—А–Є–є—Б–Ї–Є–є –≥–µ–Њ–і–µ–Ј–Є—Б—В –У.–Ь–Њ—А–Є—Ж —В–∞–Ї –Њ—В–Њ–Ј–≤–∞–ї—Б—П –Њ —А–∞–±–Њ—В–µ –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ: вМ†–Ъ–Њ–≥–і–∞ –±–ї–µ—Б—В—П—Й–∞—П —А–∞–±–Њ—В–∞ –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ —Б—В–∞–ї–∞ –Є–Ј–≤–µ—Б—В–љ–Њ–є –љ–∞ –Ј–∞–њ–∞–і–µ, –Њ–љ–∞ –њ—А–Њ–Є–Ј–≤–µ–ї–∞ –њ–Њ–Є—Б—В–Є–љ–µ —А–µ–≤–Њ–ї—О—Ж–Є—О –Ъ–Њ–њ–µ—А–љ–Є–Ї–∞ –≤ —Г–Љ–∞—Е –≥–µ–Њ–і–µ–Ј–Є—Б—В–Њ–≤ –≤—Б–µ—Е —Б—В—А–∞–љвФШвЦ† (–У.–Ь–Њ—А–Є—Ж .–°–Њ–≤—А–µ–Љ–µ–љ–љ–∞—П —Д–Є–Ј–Є—З–µ—Б–Ї–∞—П –≥–µ–Њ–і–µ–Ј–Є—П. –Ь–Њ—Б–Ї–≤–∞ вМ†–Э–µ–і—А–∞вЦ† 1983). –≠—В–∞ —А–∞–±–Њ—В–∞ —Б—В–Є–Љ—Г–ї–Є—А–Њ–≤–∞–ї–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –≤ –Њ–±–ї–∞—Б—В–Є —В–µ–Њ—А–Є–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Э–∞ –≤–Њ–Њ—А—Г–ґ–µ–љ–Є–µ –≤–Ј—П—В—Л —В–∞–Ї–Є–µ —Б–µ—А—МвХ¶–Ј–љ—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –і–Є—Б—Ж–Є–њ–ї–Є–љ—Л –Ї–∞–Ї —В–µ–Њ—А–Є—П —Д—Г–љ–Ї—Ж–Є–є, —В–µ–Њ—А–Є—П –≥—А—Г–њ–њ, –Є–љ—В–µ–≥—А–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П, –Љ–∞—В—А–Є—З–љ–Њ-—В–µ–љ–Ј–Њ—А–љ—Л–є –∞–љ–∞–ї–Є–Ј –Є –і—А. –Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ, —Б–Њ–≤–µ—В—Б–Ї–Є–µ —Г—З–µ–љ—Л–µ –Ы.–Я.–Я–µ–ї–ї–Є–љ–µ–љ, –Т.–Т.–С—А–Њ–≤–∞—А, –Ь.–Ѓ.–Э–µ–є–Љ–∞–љ —Е–Њ—А–Њ—И–Њ –Є–Ј–≤–µ—Б—В–љ—Л –≤ –Љ–Є—А–Њ–≤–Њ–Љ —Б–Њ–Њ–±—Й–µ—Б—В–≤–µ —Г—ЗвХ¶–љ—Л—Е.
–Я–Њ—П–≤–ї–µ–љ–Є–µ —Б–њ—Г—В–љ–Є–Ї–Њ–≤ –Є –љ–Њ–≤—Л—Е –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В–µ–є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ —А–∞—Б—И–Є—А–Є–ї–Њ –Ї—А—Г–≥ –Ј–∞–і–∞—З —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є. –Я–Њ—П–≤–Є–ї–Њ—Б—М –љ–Њ–≤–Њ–µ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –≤ –≤—Л—Б—И–µ–є –≥–µ–Њ–і–µ–Ј–Є–Є ¾
–Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–∞—П –≥–µ–Њ–і–µ–Ј–Є—П. –Х—Б–ї–Є —А–∞–љ—М—И–µ —В—А–Є–∞–љ–≥—Г–ї—П—Ж–Є—П —А–∞–Ј–≤вХ¶—А—В—Л–≤–∞–ї–∞—Б—М –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є, —В–Њ —Б–µ–є—З–∞—Б –Њ–љ–∞ —Б—В–∞–ї–∞ —В—А–µ—Е–Љ–µ—А–љ–Њ–є. –Ъ–Њ—Б–Љ–Є—З–µ—Б–Ї–Є–µ —В—А–Є–∞–љ–≥—Г–ї—П—Ж–Є–Њ–љ–љ—Л–µ –њ—Г–љ–Ї—В—Л ¾
–њ—Г–љ–Ї—В—Л —Б–ї–µ–ґ–µ–љ–Є—П –Ј–∞ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ–Є —Б–њ—Г—В–љ–Є–Ї–∞–Љ–Є. –Ф–≤–Є–ґ–µ–љ–Є–µ —Б–њ—Г—В–љ–Є–Ї–Њ–≤, –Ї–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ, –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї –і–≤–Є–ґ–µ–љ–Є–µ –њ–Њ –љ–µ–Ї–Њ—В–Њ—А–Њ–є –Њ—А–±–Є—В–µ –≤–Њ–Ї—А—Г–≥ —Ж–µ–љ—В—А–∞ –Љ–∞—Б—Б. –Я–Њ—Н—В–Њ–Љ—Г –Ј–∞ –љ–∞—З–∞–ї–Њ —Б–Є—Б—В–µ–Љ—Л –Њ—В—Б—ЗвХ¶—В–∞ –±–µ—А—Г—В —Ж–µ–љ—В—А –Љ–∞—Б—Б. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ —Н—В–Є—Е –њ—Г–љ–Ї—В–Њ–≤ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —В–µ–ї–∞ –Њ—В—Б—З–µ—В–∞, –Ї–Њ—В–Њ—А—Л–Љ —Б–ї—Г–ґ–Є—В –Њ–±—Й–Є–є –Ј–µ–Љ–љ–Њ–є —Н–ї–ї–Є–њ—Б–Њ–Є–і. –Т–Ј–∞–Є–Љ–љ–Њ–µ —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –њ—Г–љ–Ї—В–Њ–≤ –Ј–∞–і–∞—О—В –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є B,L,H, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, —И–Є—А–Њ—В–Њ–є, –і–Њ–ї–≥–Њ—В–Њ–є –Є –≤—Л—Б–Њ—В–Њ–є. –§—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ–Њ –Ј–∞–і–∞—З–µ–є —П–≤–ї—П–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Ж–µ–љ—В—А–∞ –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Ж–µ–љ—В—А–∞ –Љ–∞—Б—Б.
–Т –і–Њ—Б–њ—Г—В–љ–Є–Ї–Њ–≤—Г—О —Н–њ–Њ—Е—Г –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —А–∞–±–Њ—В—Л –≤–њ–Њ–ї–љ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–ї–∞ –њ—А–Є–≤—П–Ј–Ї–∞ –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г, –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А—Г—О—Й–µ–Љ—Г –Є—Б—Б–ї–µ–і—Г–µ–Љ—Г—О —В–µ—А—А–Є—В–Њ—А–Є—О. –°–Њ–≤–µ—В—Б–Ї–Є–є –≥–µ–Њ–і–µ–Ј–Є—Б—В –§.–Ь.–Ъ—А–∞—Б–Њ–≤—Б–Ї–Є–є –њ–Њ–ї—Г—З–Є–ї –њ–∞—А–∞–Љ–µ—В—А—Л —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –і–ї—П –°–Њ–≤–µ—В—Б–Ї–Њ–≥–Њ –°–Њ—О–Ј–∞ —Б –љ–∞—З–∞–ї–Њ–Љ –Њ—В—Б—З–µ—В–∞ –≤—Л—Б–Њ—В –њ–Њ –Ъ—А–Њ–љ—И—В–∞–і—Б–Ї–Њ–Љ—Г —Д—Г—В—И—В–Њ–Ї—Г. –°–ґ–∞—В–Є–µ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Ъ—А–∞—Б–Њ–≤—Б–Ї–Њ–≥–Њ —А–∞–≤–љ–Њ 1:298,3 , –≠—В–∞ –≤–µ–ї–Є—З–Є–љ–∞ –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –Њ—В–ї–Є—З–∞–ї–∞—Б—М –Њ—В —Б–ґ–∞—В–Є—П –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –њ—А–Є–љ—П—В–Њ–≥–Њ –≤ —В–Њ –≤—А–µ–Љ—П –Є –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ –њ–Њ –≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ –і–∞–љ–љ—Л–Љ. –Р–≤—В–Њ—А—Л –і–∞–≤–∞–ї–Є —А–∞–Ј–љ—Л–µ –Њ—Ж–µ–љ–Ї–Є —Б–ґ–∞—В–Є—П –Њ—В 1:296,6 –і–Њ 1:297,4. –Я–µ—А–≤–Њ–µ –ґ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Б–ґ–∞—В–Є—П –њ–Њ —Б–њ—Г—В–љ–Є–Ї–Њ–≤—Л–Љ –і–∞–љ–љ—Л–Љ –і–∞–ї–Њ –≤–µ–ї–Є—З–Є–љ—Г, –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є —Б–Њ–≤–њ–∞–і–∞—О—Й—Г—О —Б–Њ —Б–ґ–∞—В–Є–µ–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Ъ—А–∞—Б–Њ–≤—Б–Ї–Њ–≥–Њ. –Ґ–Њ—З–љ–Њ—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –≤–Њ–Ј—А–Њ—Б–ї–∞. –У–µ–љ–µ—А–∞–ї—М–љ–∞—П –Р—Б—Б–∞–Љ–±–ї–µ—П –Ь–Р–° –≤ 1976 –≥ –і–ї—П —Б–ґ–∞—В–Є—П –Ч–µ–Љ–ї–Є —Г—В–≤–µ—А–і–Є–ї–∞ –Ј–љ–∞—З–µ–љ–Є–µ 1:298,2570.
–°–њ—Г—В–љ–Є–Ї–Њ–≤—Л–µ –∞–ї—М—В–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –і–∞–ї–Є –њ—А—П–Љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П —В–Њ–њ–Њ–≥—А–∞—Д–Є–Є –≤–Њ–і–љ–Њ–є –≥–ї–∞–і–Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ–Ї–µ–∞–љ–Њ–≤, –Ї–Њ—В–Њ—А–∞—П —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –≥–µ–Њ–Є–і–Њ–Љ —Б —В–Њ—З–љ–Њ—Б—В—М—О
+1–Љ. –°–∞–Љ–Є –∞–ї—М—В–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ –љ–∞–±–ї—О–і–µ–љ–Є—П –і–Њ—Б—В–Є–≥–ї–Є —В–Њ—З–љ–Њ—Б—В–Є –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е —Б–∞–љ—В–Є–Љ–µ—В—А–Њ–≤. –Я–Њ—П–≤–Є–ї–∞—Б—М –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ—Б—В—М —Б —В–∞–Ї–Њ–є –ґ–µ —В–Њ—З–љ–Њ—Б—В—М—О —Б—В—А–Њ–Є—В—М –Є —В–µ–Њ—А–Є—О –і–≤–Є–ґ–µ–љ–Є—П —Б–њ—Г—В–љ–Є–Ї–Њ–≤ –Є –Њ–њ—А–µ–і–µ–ї—П—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –≥–µ–Њ–Є–і–∞. –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–µ –ї–Є–љ–µ–є–љ–Њ–µ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–µ —Б —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ –њ–µ—А–≤–Њ–є —Б—В–µ–њ–µ–љ–Є —Б–ґ–∞—В–Є—П —Б—В–∞–ї–Њ –љ–µ–њ—А–Є–µ–Љ–ї–µ–Љ—Л–Љ. –Х—Б–ї–Є —А–∞–і–Є—Г—Б –Ч–µ–Љ–ї–Є —А–∞–≤–µ–љ R, —В–Њ –Љ–∞–ї—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є –Љ—Л –і–Њ–ї–ґ–љ—Л —Б—З–Є—В–∞—В—М –ї–Є–љ–µ–є–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л 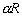 »
20 –Ї–Љ. –Ь–∞–ї—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –±—Г–і—Г—В
»
20 –Ї–Љ. –Ь–∞–ї—Л–Љ–Є –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –±—Г–і—Г—В 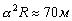 , –∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ ¾
, –∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ ¾
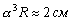 . –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —В–µ–Њ—А–Є—П –і–≤–Є–ґ–µ–љ–Є—П —Б–њ—Г—В–љ–Є–Ї–Њ–≤ –і–Њ–ї–ґ–љ–∞ –Њ–±–µ—Б–њ–µ—З–Є–≤–∞—В—М —Б–∞–љ—В–Є–Љ–µ—В—А–Њ–≤—Г—О —В–Њ—З–љ–Њ—Б—В—М, –∞ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–∞—П —В–µ–Њ—А–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є –і–Њ–ї–ґ–љ–∞ —Б—В—А–Њ–Є—В—М—Б—П —В–∞–Ї, —З—В–Њ–±—Л –Њ–±–µ—Б–њ–µ—З–Є—В—М —В–Њ—З–љ–Њ—Б—В—М –і–Њ –Љ–∞–ї—Л—Е —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Ъ —Б–Њ–ґ–∞–ї–µ–љ–Є—О, —В–∞–Ї–Є—Е —В–Њ—З–љ–Њ—Б—В–µ–є –µ—ЙвХ¶ –љ–µ –њ–Њ–ї—Г—З–µ–љ–Њ.
. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —В–µ–Њ—А–Є—П –і–≤–Є–ґ–µ–љ–Є—П —Б–њ—Г—В–љ–Є–Ї–Њ–≤ –і–Њ–ї–ґ–љ–∞ –Њ–±–µ—Б–њ–µ—З–Є–≤–∞—В—М —Б–∞–љ—В–Є–Љ–µ—В—А–Њ–≤—Г—О —В–Њ—З–љ–Њ—Б—В—М, –∞ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–∞—П —В–µ–Њ—А–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є –і–Њ–ї–ґ–љ–∞ —Б—В—А–Њ–Є—В—М—Б—П —В–∞–Ї, —З—В–Њ–±—Л –Њ–±–µ—Б–њ–µ—З–Є—В—М —В–Њ—З–љ–Њ—Б—В—М –і–Њ –Љ–∞–ї—Л—Е —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Ъ —Б–Њ–ґ–∞–ї–µ–љ–Є—О, —В–∞–Ї–Є—Е —В–Њ—З–љ–Њ—Б—В–µ–є –µ—ЙвХ¶ –љ–µ –њ–Њ–ї—Г—З–µ–љ–Њ.
–Ы–µ–Ї—Ж–Є—П 2
–°—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞. –®–Є—А–Њ—В–∞ –і–Њ–ї–≥–Њ—В–∞ –Є —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А. –°–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В, –њ–Њ—Б—В—А–Њ–µ–љ–љ–∞—П –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ
–Ї–Њ–Њ—А–і–Є–љ–∞—В—Л: —И–Є—А–Њ—В–∞, –і–Њ–ї–≥–Њ—В–∞ –Є –≤—Л—Б–Њ—В–∞. –°–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є, –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є –Є –і–µ–Ї–∞—А—В–Њ–≤–Њ–є —Б–Є—Б—В–µ–Љ–∞–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В.
–У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В
–≠–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ –Ј–∞–і–∞—З–Є —А–µ—И–∞—О—В –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –µ—Б–ї–Є —А–∞–Ј–Љ–µ—А—Л
–њ–ї–Њ—Й–∞–і–Є –љ–µ–≤–µ–ї–Є–Ї–Є. –Х—Б–ї–Є –Є—Б—Б–ї–µ–і—Г–µ–Љ–∞—П —З–∞—Б—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ј–∞–љ–Є–Љ–∞–µ—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –≥—А–∞–і—Г—Б–Њ–≤ —И–Є—А–Њ—В—Л –Є–ї–Є –і–Њ–ї–≥–Њ—В—Л, —В–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Г—З–Є—В—Л–≤–∞—В—М –Є –Ї—А–Є–≤–Є–Ј–љ—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —З–∞—Б—В–Њ –њ–Њ–і—Е–Њ–і–Є—В –Є —И–∞—А. –Ф–ї—П —А–µ—И–µ–љ–Є—П –≥–ї–Њ–±–∞–ї—М–љ—Л—Е –Ј–∞–і–∞—З, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –Є –Ј–∞–і–∞—З –њ–Њ –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–є –≥–µ–Њ–і–µ–Ј–Є–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ —В–µ–ї–∞ –Њ—В—Б—ЗвХ¶—В–∞ –±–µ—А—Г—В —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П. –Т —З–∞—Б—В–љ–Њ—Б—В–Є –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ —А–µ—И–∞—О—В —Б–ї–µ–і—Г—О—Й–Є–µ –Ј–∞–і–∞—З–Є:
–£—В–Њ—З–љ–µ–љ–Є–µ —Д–Њ—А–Љ—Л –Є —А–∞–Ј–Љ–µ—А–Њ–≤ –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ (–Ю–Ч–≠).
-–Я–µ—А–µ–љ–Њ—Б –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–є –Є —А–∞—Б—Б—В–Њ—П–љ–Є–є —Б —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і.
-–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В —В–Њ—З–µ–Ї –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–µ—Д–µ—А–µ–љ—Ж-—Н–ї–ї–Є–њ—Б–Њ–Є–і–∞.
-–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —А–∞—Б—Б—В–Њ—П–љ–Є–є –Љ–µ–ґ–і—Г —В–Њ—З–Ї–∞–Љ–Є —Б –Ј–∞–і–∞–љ–љ—Л–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є.
-–£—В–Њ—З–љ–µ–љ–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –њ–Њ –Љ–µ—А–µ —Г—В–Њ—З–љ–µ–љ–Є—П —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞.
–Ф–µ–Ї–∞—А—В–Њ–≤—Л —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В
–Т–≤–µ–івХ¶–Љ –і–≤–µ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В: –ї–Њ–Ї–∞–ї—М–љ—Г—О –Є –≥–ї–Њ–±–∞–ї—М–љ—Г—О.
–Э–∞—З–∞–ї–Њ —Б–Є—Б—В–µ–Љ—Л –Њ—В—Б—З–µ—В–∞ (—В–Њ—З–Ї–∞ –†) –і–ї—П –ї–Њ–Ї–∞–ї—М–љ–Њ–є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В –≤—Л–±–µ—А–µ–Љ –≤ —В–Њ—З–Ї–µ –љ–∞–±–ї—О–і–µ–љ–Є—П, –ї–µ–ґ–∞—Й–µ–є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Ю—Б—М –†–• –љ–∞–њ—А–∞–≤–Є–Љ –љ–∞ –°–µ–≤–µ—А, –Њ—Б—М –†–£ ¾
–љ–∞ –Т–Њ—Б—В–Њ–Ї, –∞ –Њ—Б—М
PZ –њ–Њ –љ–Њ—А–Љ–∞–ї–Є –Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤–љ–Є–Ј (–њ–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є –љ–Њ—А–Љ–∞–ї–Є). –Т —Н—В–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В вМ†–≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–∞—ПвЦ† –њ–ї–Њ—Б–Ї–Њ—Б—В—М –•–†–£ –љ–µ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞.
–У–ї–Њ–±–∞–ї—М–љ—Г—О –і–µ–Ї–∞—А—В–Њ–≤—Г –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В
Oxyz —Б—В—А–Њ—П—В —В–∞–Ї. –Э–∞—З–∞–ї–Њ –Њ—В—Б—З–µ—В–∞ —Б–Њ–≤–Љ–µ—Й–∞—О—В —Б —Ж–µ–љ—В—А–Њ–Љ –Ю–Ч–≠ (–љ–µ –њ—Г—В–∞—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б –Ч–µ–Љ–ї–Є!), –њ–ї–Њ—Б–Ї–Њ—Б—В—М xOy - c –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞. –Ю—Б—М Ox —Б–Њ–≤–Љ–µ—Й–∞—О—В —Б –ї–Є–љ–Є–µ–є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –љ—Г–ї–µ–≤–Њ–≥–Њ –Љ–µ—А–Є–і–Є–∞–љ–∞ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Н–Ї–≤–∞—В–Њ—А–∞. –Ю—Б—М Oy –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Н–Ї–≤–∞—В–Њ—А –≤ —В–Њ—З–Ї–µ —Б –і–Њ–ї–≥–Њ—В–Њ–є 90°
. –Ю—Б—М Oz —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П –Ю–Ч–≠. –≠—В–∞ –Њ—Б—М –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є. –Ф–ї—П —В—А–µ—Е–Њ—Б–љ–Њ–≥–Њ –Ю–Ч–≠ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В –±–µ—А—Г—В –≤ —Ж–µ–љ—В—А–µ –Љ–∞—Б—Б –Ч–µ–Љ–ї–Є, –∞ –Њ—Б–Є вИЪ —Б–Њ–≤–њ–∞–і–∞—О—Й–Є–Љ–Є —Б –≥–ї–∞–≤–љ—Л–Љ–Є –Њ—Б—П–Љ–Є –Є–љ–µ—А—Ж–Є–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –њ–ї–Њ—Б–Ї–Њ—Б—В—М xOy , –≤–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, –љ–µ –±—Г–і–µ—В –ї–µ–ґ–∞—В—М –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Н–Ї–≤–∞—В–Њ—А–∞.
–°—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–Ґ–µ–ї–Њ–Љ –Њ—В—Б—З–µ—В–∞ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В —П–≤–ї—П–µ—В—Б—П —Б—Д–µ—А–∞ —Б —А–∞–і–Є—Г—Б–Њ–Љ
R. –Э–∞—З–∞–ї–Њ —Н—В–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ–≤–Љ–µ—Й–∞—О—В —Б —Ж–µ–љ—В—А–Њ–Љ —Б—Д–µ—А—Л. –Ъ–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є —П–≤–ї—П—О—В—Б—П –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П —И–Є—А–Њ—В–∞ –§, –і–Њ–ї–≥–Њ—В–∞ 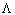 –Є —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А r. –®–Є—А–Њ—В–Њ–є –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Г–≥–Њ–ї –Љ–µ–ґ–і—Г —А–∞–і–Є—Г—Б–Њ–Љ-–≤–µ–Ї—В–Њ—А–Њ–Љ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞. –Ф–Њ–ї–≥–Њ—В–∞ –µ—Б—В—М —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г –Є –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П (–њ–ї–Њ—Б–Ї–Њ—Б—В—М –Љ–µ—А–Є–і–Є–∞–љ–∞) –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –Љ–µ—А–Є–і–Є–∞–љ–∞, –њ—А–Є–љ—П—В–Њ–≥–Њ –≤ –Ї–∞—З–µ—Б—В–≤–µ –љ—Г–ї–µ–≤–Њ–≥–Њ. –°–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є –Є –≥–ї–Њ–±–∞–ї—М–љ–Њ–є –і–µ–Ї–∞—А—В–Њ–≤–Њ–є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–∞–Љ–Є
–Є —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А r. –®–Є—А–Њ—В–Њ–є –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Г–≥–Њ–ї –Љ–µ–ґ–і—Г —А–∞–і–Є—Г—Б–Њ–Љ-–≤–µ–Ї—В–Њ—А–Њ–Љ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞. –Ф–Њ–ї–≥–Њ—В–∞ –µ—Б—В—М —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г –Є –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П (–њ–ї–Њ—Б–Ї–Њ—Б—В—М –Љ–µ—А–Є–і–Є–∞–љ–∞) –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –Љ–µ—А–Є–і–Є–∞–љ–∞, –њ—А–Є–љ—П—В–Њ–≥–Њ –≤ –Ї–∞—З–µ—Б—В–≤–µ –љ—Г–ї–µ–≤–Њ–≥–Њ. –°–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є –Є –≥–ї–Њ–±–∞–ї—М–љ–Њ–є –і–µ–Ї–∞—А—В–Њ–≤–Њ–є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–∞–Љ–Є
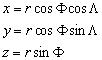 (1)
(1)
–Т —В–Њ–Љ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ —И–Є—А–Њ—В–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞ –Є –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–µ–є, —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Њ–є. –®–Є—А–Њ—В–∞ –Є –і–Њ–ї–≥–Њ—В–∞, –Њ–њ—А–µ–і–µ–ївХ¶–љ–љ—Л–µ –≤ —Н—В–Њ–є —Б–Є—Б—В–µ–Љ–µ –Љ—Л –±—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М —З–µ—А–µ–Ј
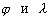 .
.
–У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–° –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В
B, L ,H —Б–≤—П–Ј—Л–≤–∞—О—В –њ–Њ–љ—П—В–Є—П –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є —И–Є—А–Њ—В—Л, –і–Њ–ї–≥–Њ—В—Л –Є –≤—Л—Б–Њ—В—Л. –У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П —И–Є—А–Њ—В–∞ –Т –µ—Б—В—М —Г–≥–Њ–ї, –њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П –љ–Њ—А–Љ–∞–ї—М –Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —Б –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞. –Ф–Њ–ї–≥–Њ—В–∞ L - –і–≤—Г–≥—А–∞–љ–љ—Л–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –љ—Г–ї–µ–≤–Њ–≥–Њ –Љ–µ—А–Є–і–Є–∞–љ–∞ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –Љ–µ—А–Є–і–Є–∞–љ–∞, –њ—А–Њ—Е–Њ–і—П—Й–µ–≥–Њ —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г.
–У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —И–Є—А–Њ—В–∞ –Є –і–Њ–ї–≥–Њ—В–∞ –Њ—В–ї–Є—З–∞—О—В—Б—П –Њ—В —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В, —Б–≤—П–Ј–∞–љ–љ—Л—Е —Б –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–µ–є, —В–∞–Ї –Ї–∞–Ї –Њ—В–≤–µ—Б–љ–∞—П –ї–Є–љ–Є—П –љ–µ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –љ–Њ—А–Љ–∞–ї—М—О –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г. –Ю—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є –Љ–Њ–ґ–љ–Њ —Б–њ—А–Њ–µ—Ж–Є—А–Њ–≤–∞—В—М –љ–∞ –і–≤–µ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є: –њ–ї–Њ—Б–Ї–Њ—Б—В—М –Љ–µ—А–Є–і–Є–∞–љ–∞ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М –њ–µ—А–≤–Њ–≥–Њ –≤–µ—А—В–Є–Ї–∞–ї–∞. –Э–µ—В—А—Г–і–љ–Њ –њ–Њ–љ—П—В—М, —З—В–Њ –Њ–±–µ —Н—В–Є —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —З–µ—А–µ–Ј —А–∞–Ј–љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–Љ–Є –Є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є
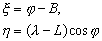 . (2)
. (2)
–Ю—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є —Б–Њ—Б—В–∞–≤–ї—П—О—В, –Ї–∞–Ї –њ—А–∞–≤–Є–ї–Њ, –њ–µ—А–≤—Л–µ –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б–µ–Ї—Г–љ–і –і—Г–≥–Є.
–У–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П –Є –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П –і–Њ–ї–≥–Њ—В—Л —Б–Њ–≤–њ–∞–і–∞—О—В. –Ю–±–µ –Њ–љ–Є –Њ–њ—А–µ–і–µ–ї–µ–љ—Л –Ї–∞–Ї –і–≤—Г–≥—А–∞–љ–љ—Л–є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –љ—Г–ї–µ–≤–Њ–≥–Њ –Љ–µ—А–Є–і–Є–∞–љ–∞ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О, —Б–Њ–і–µ—А–ґ–∞—Й–µ–є –Њ—Б—М –≤—А–∞—Й–µ–љ–Є—П –Є –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г. –У–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П –ґ–µ —И–Є—А–Њ—В–∞ –Њ—В–ї–Є—З–∞–µ—В—Б—П –Њ—В –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–Њ—З–Ї—Г
P, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Ю–Ч–≠. –Ю–њ—Г—Б—В–Є–Љ –Є–Ј —Н—В–Њ–є —В–Њ—З–Ї–Є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є –њ—А–Њ–і–Њ–ї–ґ–Є–Љ –µ–≥–Њ –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О (—А–Є—Б2) –Я—А–Њ–µ–Ї—Ж–Є—О —В–Њ—З–Ї–Є P –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Њ–±–Њ–Ј–љ–∞—З–Є–Љ —З–µ—А–µ–Ј Q. –Ґ–Њ–≥–і–∞ –Њ—В—А–µ–Ј–Њ–Ї PQ –µ—Б—В—М –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П –≤—Л—Б–Њ—В–∞ —В–Њ—З–Ї–Є –†. –£–≥–Њ–ї, –њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ —Г–њ–Њ–Љ—П–љ—Г—В—Л–є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –њ–ї–Њ—Б–Ї–Њ—Б—В—М —Н–Ї–≤–∞—В–Њ—А–∞, –µ—Б—В—М –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П —И–Є—А–Њ—В–∞ B. –Ю–љ–∞ –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї–∞–Ї –Ї —В–Њ—З–Ї–µ Q, —В–∞–Ї –Є –Ї —В–Њ—З–Ї–µ –†. –У–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–Є–µ —И–Є—А–Њ—В—Л —Н—В–Є—Е –і–≤—Г—Е —В–Њ—З–µ–Ї, –Ї–∞–Ї –≤–Є–і–љ–Њ –Є–Ј —А–Є—Б—Г–љ–Ї–∞, —А–∞–Ј–ї–Є—З–∞—О—В—Б—П. –У–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П —И–Є—А–Њ—В–∞ —В–Њ—З–Ї–Є Q —Г–≥–Њ–ї –§ –Љ–µ–ґ–і—Г —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А–Њ–Љ —Н—В–Њ–є —В–Њ—З–Ї–Є –Є –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О —Н–Ї–≤–∞—В–Њ—А–∞.
–£—Б—В–∞–љ–Њ–≤–Є–Љ —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є —В–Њ—З–Ї–Є
Q, —Б–ґ–∞—В–Є–µ–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ 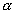 –Є —И–Є—А–Њ—В–∞–Љ–Є –Т –Є –§. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —В–Њ—З–Ї–∞ Q –ї–µ–ґ–Є—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, —В–Њ –µвХ¶ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л
–Є —И–Є—А–Њ—В–∞–Љ–Є –Т –Є –§. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —В–Њ—З–Ї–∞ Q –ї–µ–ґ–Є—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, —В–Њ –µвХ¶ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л 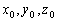 –њ–Њ–і—З–Є–љ—П—О—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є—О —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П:
–њ–Њ–і—З–Є–љ—П—О—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є—О —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П:  . –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–µ—З–µ–љ–Є–µ y=0. –Ґ–Њ–≥–і–∞, –Ї–∞–Ї –ї–µ–≥–Ї–Њ –≤–Є–і–µ—В—М,
. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–µ—З–µ–љ–Є–µ y=0. –Ґ–Њ–≥–і–∞, –Ї–∞–Ї –ї–µ–≥–Ї–Њ –≤–Є–і–µ—В—М, 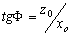 . –І—В–Њ–±—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М tg–Т, –љ—Г–ґ–љ–Њ –љ–∞–є—В–Є —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –љ–Њ—А–Љ–∞–ї–Є –≤ —В–Њ—З–Ї–µ Q. –£—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є –Ї –Ї—А–Є–≤–Њ–є F(x ,z) =0 –≤ —В–Њ—З–Ї–µ
. –І—В–Њ–±—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М tg–Т, –љ—Г–ґ–љ–Њ –љ–∞–є—В–Є —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –љ–Њ—А–Љ–∞–ї–Є –≤ —В–Њ—З–Ї–µ Q. –£—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є –Ї –Ї—А–Є–≤–Њ–є F(x ,z) =0 –≤ —В–Њ—З–Ї–µ 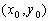 –Є–Љ–µ–µ—В –≤–Є–і
–Є–Љ–µ–µ—В –≤–Є–і
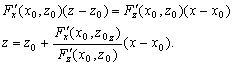 (3)
(3)
–£ –љ–∞—Б

–њ–Њ—Н—В–Њ–Љ—Г
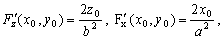
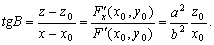
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
, 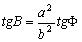
–Ю–њ—А–µ–і–µ–ї–Є–Љ –Њ—В–ї–Є—З–Є–µ –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–Њ–є —И–Є—А–Њ—В—Л –§ –Њ—В –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є –Т
. –Ш–Љ–µ–µ–Љ –Њ—З–µ–≤–Є–і–љ—Л–µ —А–∞–≤–µ–љ—Б—В–≤–∞
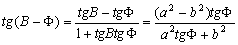 . (4)
. (4)
–Т—В–Њ—А–Њ–є —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В —Н–ї–ї–Є–њ—Б–∞, –Ї–∞–Ї –Љ—Л –Ј–љ–∞–µ–Љ, –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
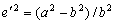 , –њ–Њ—Н—В–Њ–Љ—Г
, –њ–Њ—Н—В–Њ–Љ—Г
 .
.
–Ф–ї—П –Ч–µ–Љ–ї–Є –≤—В–Њ—А–Њ–є —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В –Љ–∞–ї, –њ–Њ—Н—В–Њ–Љ—Г, –њ—А–µ–љ–µ–±—А–µ–≥–∞—П –Љ–∞–ї—Л–Љ–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Б–ґ–∞—В–Є—П, –њ–Њ–ї—Г—З–Є–Љ
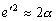 . –Ь–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ —Б—З–Є—В–∞—В—М, —З—В–Њ
. –Ь–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ —Б—З–Є—В–∞—В—М, —З—В–Њ 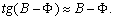 –£—З–Є—В—Л–≤–∞—П —Б–Ї–∞–Ј–∞–љ–љ–Њ–µ, –њ–Њ–ї—Г—З–Є–Љ
–£—З–Є—В—Л–≤–∞—П —Б–Ї–∞–Ј–∞–љ–љ–Њ–µ, –њ–Њ–ї—Г—З–Є–Љ 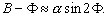
–Э–∞–Є–±–Њ–ї—М—И–µ–µ –Њ—В–ї–Є—З–Є–µ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є —И–Є—А–Њ—В—Л –Њ—В –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–Њ–є –і–Њ—Б—В–Є–≥–∞–µ—В—Б—П –љ–∞ —И–Є—А–Њ—В–µ 45°
–Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В
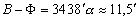 .
.
–°–≤—П–Ј—М –≥–ї–Њ–±–∞–ї—М–љ—Л—Е –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–Є–Љ–Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–∞–Љ–Є (1). –Ю–њ—А–µ–і–µ–ї–Є–Љ —В–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Л, —Б–≤—П–Ј—Л–≤–∞—О—Й–Є–µ –і–µ–Ї–∞—А—В–Њ–≤—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —Б –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ–Є. –≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –±—Л –і–Њ–ї–ґ–љ—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є –† —З–µ—А–µ–Ј –њ–∞—А–∞–Љ–µ—В—А—Л —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —И–Є—А–Њ—В—Г –Є –і–Њ–ї–≥–Њ—В—Г.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
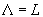 , –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Ї–Њ–Њ—А–і–Є–љ–∞—В x, y ,z —В–Њ—З–Ї–Є –† –і–Њ—Б—В–∞—В–Њ—З–љ–Њ, –і–ї—П –љ–∞—З–∞–ї–∞, –Њ–њ—А–µ–і–µ–ї–Є—В—М —В–Њ–ї—М–Ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л x –Є z . —В–Њ –µ—Б—В—М –≤—Б–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –њ—А–Њ–≤–Њ–і–Є—В—М —В–Њ–ї—М–Ї–Њ –і–ї—П —Б–µ—З–µ–љ–Є—П —Г =0. –Ю–±—А–∞—В–Є–Љ—Б—П –Ї —А–Є—Б. 3.
, –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Ї–Њ–Њ—А–і–Є–љ–∞—В x, y ,z —В–Њ—З–Ї–Є –† –і–Њ—Б—В–∞—В–Њ—З–љ–Њ, –і–ї—П –љ–∞—З–∞–ї–∞, –Њ–њ—А–µ–і–µ–ї–Є—В—М —В–Њ–ї—М–Ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л x –Є z . —В–Њ –µ—Б—В—М –≤—Б–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –њ—А–Њ–≤–Њ–і–Є—В—М —В–Њ–ї—М–Ї–Њ –і–ї—П —Б–µ—З–µ–љ–Є—П —Г =0. –Ю–±—А–∞—В–Є–Љ—Б—П –Ї —А–Є—Б. 3.
–Ю–њ—А–µ–і–µ–ї–Є–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є –†, —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–љ–Њ–є –љ–∞ –≤—Л—Б–Њ—В–µ –Э –љ–∞–і –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –°–љ–∞—З–∞–ї–∞ –Њ–њ—А–µ–і–µ–ї–Є–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –њ—А–Њ–µ–Ї—Ж–Є–Є —В–Њ—З–Ї–Є –† –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ ( —В–Њ—З–Ї–∞
Q). –ХвХ¶ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤ —Б–µ—З–µ–љ–Є–Є –Ю—Еz —А–∞–≤–љ—Л
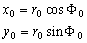
–Ш–љ–і–µ–Ї—Б–Њ–Љ вМ†0вЦ† –Љ—Л –Њ—В–Љ–µ—В–Є–ї–Є –њ—А–Є–љ–∞–і–ї–µ–ґ–љ–Њ—Б—В—М –Ї–Њ–Њ—А–і–Є–љ–∞—В –Ї —В–Њ—З–Ї–µ, –ї–µ–ґ–∞—Й–µ–є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є
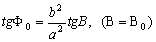
–њ–Њ—Н—В–Њ–Љ—Г
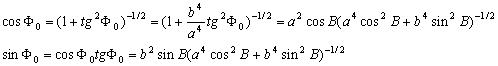
–Ю—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —В–Њ—З–Ї–Є
Q. –Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ —Н–ї–ї–Є–њ—Б–∞ –Є –≤—Л–њ–Њ–ї–љ–Є–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П.
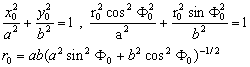 (5)
(5)
–Т—Л—А–∞–Ј–Є–Љ
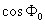 –Є
–Є 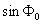 —З–µ—А–µ–Ј cosB –Є sinB, –і–ї—П —З–µ–≥–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –њ—А–Є–≤–µ–івХ¶–љ–љ—Л–Љ–Є –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї–∞–Љ–Є. –Ю–њ—А–µ–і–µ–ї–Є–Љ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —В–Њ—З–Ї–Є Q
—З–µ—А–µ–Ј cosB –Є sinB, –і–ї—П —З–µ–≥–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –њ—А–Є–≤–µ–івХ¶–љ–љ—Л–Љ–Є –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї–∞–Љ–Є. –Ю–њ—А–µ–і–µ–ї–Є–Љ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —В–Њ—З–Ї–Є Q
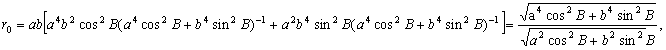
—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
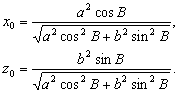 (6)
(6)
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ
 . (7)
. (7)
–Ґ–µ–њ–µ—А—М
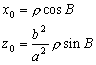 (8)
(8)
–Ф–ї—П –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П, –њ—А–Њ—Е–Њ–і—П—Й–µ–≥–Њ —З–µ—А–µ–Ј –Њ—Б—М –≤—А–∞—Й–µ–љ–Є—П
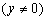 ,–±—Г–і–µ–Љ –Є–Љ–µ—В—М
,–±—Г–і–µ–Љ –Є–Љ–µ—В—М
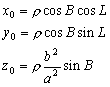 (9)
(9)
–Ґ–µ–њ–µ—А—М –њ–Њ–і–љ–Є–Љ–µ–Љ —В–Њ—З–Ї—Г
Q –љ–∞ –≤—Л—Б–Њ—В—Г –Э –Є —Б–Њ–≤–Љ–µ—Б—В–Є–Љ –µвХ¶ —Б —В–Њ—З–Ї–Њ–є –†. –Я—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є–Ј–Љ–µ–љ—П—В—Б—П –љ–∞
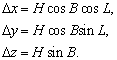 (10)
(10)
–Ю–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ, —В–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Л –і–ї—П –њ–µ—А–µ—Б—ЗвХ¶—В–∞ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В
B, L –Є –Э –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ x,y,z –њ—А–Є–Љ—Г—В –≤–Є–і
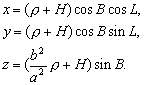 (11)
(11)
–Ч–і–µ—Б—М
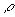 , –Њ–њ—А–µ–і–µ–ївХ¶–љ–љ—Л–є —Д–Њ—А–Љ—Г–ї–Њ–є (7) –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: –Њ–љ —А–∞–≤–µ–љ –Њ—В—А–µ–Ј–Ї—Г –љ–Њ—А–Љ–∞–ї–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї—Г Q, –Њ—В —Н—В–Њ–є —В–Њ—З–Ї–Є –і–Њ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –µвХ¶ —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –°–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В—М —Н—В–Њ–≥–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П –і–Њ–Ї–∞–Ј–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ.
, –Њ–њ—А–µ–і–µ–ївХ¶–љ–љ—Л–є —Д–Њ—А–Љ—Г–ї–Њ–є (7) –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: –Њ–љ —А–∞–≤–µ–љ –Њ—В—А–µ–Ј–Ї—Г –љ–Њ—А–Љ–∞–ї–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї—Г Q, –Њ—В —Н—В–Њ–є —В–Њ—З–Ї–Є –і–Њ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –µвХ¶ —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –°–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В—М —Н—В–Њ–≥–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П –і–Њ–Ї–∞–Ј–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ.
–≠–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–∞—П —Б–Є—Б—В–µ–Љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –µ—ЙвХ¶ –Њ–і–љ—Г —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В, –Є–Љ–µ—О—Й—Г—О –њ—А–Є–ї–Њ–ґ–µ–љ–Є–µ –≤ —В–µ–Њ—А–Є–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞:
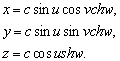
–≠—В–Є —Д–Њ—А–Љ—Г–ї—Л —Б–Њ–і–µ—А–ґ–∞—В –љ–µ —В—А–Є, –∞ —З–µ—В—Л—А–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л. –І–µ—В–≤вХ¶—А—В–∞—П –њ–µ—А–µ–Љ–µ–љ–љ–∞—П —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В —Б–µ–Љ–µ–є—Б—В–≤–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є вИЪ —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–≤. –£–±–µ–і–Є–Љ—Б—П –≤ —Н—В–Њ–Љ. –Я—А–Њ–і–µ–ї–∞–µ–Љ –њ—А–Њ—Б—В—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П:
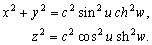
–†–∞–Ј–і–µ–ї–Є–≤ –њ–µ—А–≤–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–∞
 –∞ –≤—В–Њ—А–Њ–µ вИЪ –љ–∞
–∞ –≤—В–Њ—А–Њ–µ вИЪ –љ–∞ 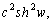 –њ–Њ–ї—Г—З–Є–Љ
–њ–Њ–ї—Г—З–Є–Љ
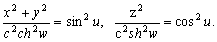
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –њ—А–Є
w=const –њ–Њ–ї—Г—З–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П
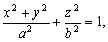
–≥–і–µ 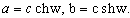
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
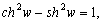 –Є–Љ–µ–µ–Љ
–Є–Љ–µ–µ–Љ 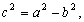 –Њ—В—Б—О–і–∞ –њ–∞—А–∞–Љ–µ—В—А —Б –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: –Њ–љ —А–∞–≤–µ–љ –њ–Њ–ї–Њ–≤–Є–љ–µ –Љ–µ–ґ—Д–Њ–Ї—Г—Б–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ –Є–Ј–Љ–µ–љ—П—П w –њ—А–Є —Г—Б–ї–Њ–≤–Є–Є —Б=const, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ —Б–Њ—Д–Њ–Ї—Г—Б–љ—Л—Е —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–≤, –Є–≥—А–∞—О—Й–Є—Е –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –≤ —В–µ–Њ—А–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –Я–Њ—Б—В—А–Њ–Є–Љ —В–µ–њ–µ—А—М —Б–µ–Љ–µ–є—Б—В–≤–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є u=const. –Я—А–Њ–і–µ–ї–∞–µ–Љ –Њ—З–µ–≤–Є–і–љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
–Њ—В—Б—О–і–∞ –њ–∞—А–∞–Љ–µ—В—А —Б –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: –Њ–љ —А–∞–≤–µ–љ –њ–Њ–ї–Њ–≤–Є–љ–µ –Љ–µ–ґ—Д–Њ–Ї—Г—Б–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ –Є–Ј–Љ–µ–љ—П—П w –њ—А–Є —Г—Б–ї–Њ–≤–Є–Є —Б=const, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ —Б–Њ—Д–Њ–Ї—Г—Б–љ—Л—Е —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–≤, –Є–≥—А–∞—О—Й–Є—Е –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –≤ —В–µ–Њ—А–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П. –Я–Њ—Б—В—А–Њ–Є–Љ —В–µ–њ–µ—А—М —Б–µ–Љ–µ–є—Б—В–≤–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є u=const. –Я—А–Њ–і–µ–ї–∞–µ–Љ –Њ—З–µ–≤–Є–і–љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
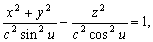
–Љ–µ–љ—П—П
u, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ –Њ–і–љ–Њ–њ–Њ–ї–Њ—Б—В–љ—Л—Е –≥–Є–њ–µ—А–±–Њ–ї–Њ–Є–і–Њ–≤ –≤—А–∞—Й–µ–љ–Є—П. –Ю–±–Њ–Ј–љ–∞—З–Є–≤ a=csinu, b=ccosu, –њ–Њ–ї—Г—З–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –≥–Є–њ–µ—А–±–Њ–ї–Њ–Є–і–∞ –≤ –Њ–±—Й–µ–њ—А–Є–љ—П—В–Њ–є —Д–Њ—А–Љ–µ. –†–∞–Ј–і–µ–ї–Є–≤ —Г –љ–∞ —Е, –њ–Њ–ї—Г—З–Є–Љ 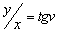 . –Ш–Ј–Љ–µ–љ—П—П v, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–µ–є, –њ—А–Њ—Е–Њ–і—П—Й–µ–µ —З–µ—А–µ–Ј –Њ—Б—М –Юz. –Т—Б–µ —В—А–Є —Б–µ–Љ–µ–є—Б—В–≤–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є –Њ–±—А–∞–Ј—Г—О—В –≤–Ј–∞–Є–Љ–љ–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г.
. –Ш–Ј–Љ–µ–љ—П—П v, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–µ–є, –њ—А–Њ—Е–Њ–і—П—Й–µ–µ —З–µ—А–µ–Ј –Њ—Б—М –Юz. –Т—Б–µ —В—А–Є —Б–µ–Љ–µ–є—Б—В–≤–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–µ–є –Њ–±—А–∞–Ј—Г—О—В –≤–Ј–∞–Є–Љ–љ–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г.
–Ы–µ–Ї—Ж–Є—П 3
–Ш–љ—В–µ–≥—А–∞–ї –Ф–Є—А–Є—Е–ї–µ, –њ–µ—А–≤–∞—П, –≤—В–Њ—А–∞—П –Є —В—А–µ—В—М—П —Д–Њ—А–Љ—Г–ї—Л –У—А–Є–љ–∞. –У–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –Є –Є—Е —Б–≤–Њ–є—Б—В–≤–∞, —В–µ–Њ—А–µ–Љ—Л –Њ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є—П—Е. –®–∞—А–Њ–≤—Л–µ –Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –Є –µ–≥–Њ —А–µ—И–µ–љ–Є–µ.
–Ю—Б–љ–Њ–≤–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л —В–µ–Њ—А–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
–Т –і–∞–љ–љ–Њ–Љ —А–∞–Ј–і–µ–ї–µ –њ–µ—А–µ—З–Є—Б–ї–Є–Љ –±–µ–Ј –≤—Л–≤–Њ–і–∞ –Њ—Б–љ–Њ–≤–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л —В–µ–Њ—А–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –Ї–Њ—В–Њ—А—Л–µ –љ–∞—Е–Њ–і—П—В –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –≤ —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є. –Ю—Б—В–∞–љ–Њ–≤–Є–Љ—Б—П –ї–Є—И—М –љ–∞ –љ–µ–Ї–Њ—В–Њ—А—Л—Е, –љ–∞–Є–±–Њ–ї–µ–µ –≤–∞–ґ–љ—Л—Е —В–µ–Њ—А–µ–Љ–∞—Е.
–Т–≤–µ–івХ¶–Љ –≤–µ–Ї—В–Њ—А–љ—Л–є –Њ–њ–µ—А–∞—В–Њ—А –љ–∞–±–ї–∞
Ñ
:
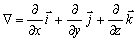 ,
,
–≥–і–µ
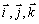 - –µ–і–Є–љ–Є—З–љ—Л–µ, –≤–Ј–∞–Є–Љ–љ–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Л–µ –≤–µ–Ї—В–Њ—А–∞.
- –µ–і–Є–љ–Є—З–љ—Л–µ, –≤–Ј–∞–Є–Љ–љ–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Л–µ –≤–µ–Ї—В–Њ—А–∞.
–° –≤–µ–Ї—В–Њ—А–љ—Л–Љ –Њ–њ–µ—А–∞—В–Њ—А–Њ–Љ –Љ–Њ–ґ–љ–Њ –Њ–±—А–∞—Й–∞—В—М—Б—П, –Ї–∞–Ї —Б –Њ–±—Л–Ї–љ–Њ–≤–µ–љ–љ—Л–Љ –≤–µ–Ї—В–Њ—А–Њ–Љ. –Э–∞–њ—А–Є–Љ–µ—А, —Б–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –і–≤—Г—Е –Њ–њ–µ—А–∞—В–Њ—А–Њ–≤ –љ–∞–±–ї–∞ –і–∞вХ¶—В –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞:
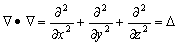 .
.
–Ф–Њ–њ—Г—Б—В–Є–Љ, —З—В–Њ –≤ –љ–∞—И–µ–Љ —А–∞—Б–њ–Њ—А—П–ґ–µ–љ–Є–Є –Є–Љ–µ–µ—В—Б—П –љ–µ–Ї–Њ—В–Њ—А–∞—П —Б–Ї–∞–ї—П—А–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П
U(x,y,z). –Ґ–Њ–≥–і–∞
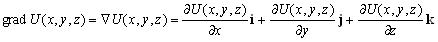
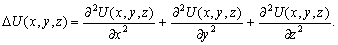
–§–Њ—А–Љ—Г–ї–∞ –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ
–° –њ–Њ–Љ–Њ—Й—М—О –Њ–њ–µ—А–∞—В–Њ—А–∞ –Ы–∞–њ–ї–∞—Б–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –њ–Њ –Њ–±—КвХ¶–Љ—Г –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ–љ–Є—В—М –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ–Љ –њ–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Т –і–∞–ї—М–љ–µ–є—И–µ–Љ –і–ї—П –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –њ—А–µ–і–µ–ї–Њ–≤ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –Љ—Л –±—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–є –њ—А–ЄвХ¶–Љ. –Т—Б–µ –і–≤—Г–Ї—А–∞—В–љ—Л–µ –Є–ї–Є —В—А–µ—Е–Ї—А–∞—В–љ—Л–µ –Є–љ—В–µ–≥—А–∞–ї—Л –Љ—Л –±—Г–і–µ–Љ –Є–Ј–Њ–±—А–∞–ґ–∞—В—М –Њ–і–љ–Њ–Ї—А–∞—В–љ—Л–Љ –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ. –Я–Њ–і –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ –±—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —Б–Є–Љ–≤–Њ–ї (S) –µ—Б–ї–Є –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –≤–µ–івХ¶—В—Б—П –њ–Њ —В–µ–ї—Г, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О
S, –Є–ї–Є –њ—А–Њ—Б—В–Њ –Ј–љ–∞—З–Ї–Њ–Љ S, –µ—Б–ї–Є –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –≤–µ–івХ¶—В—Б—П –њ–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S. –° —Н—В–Є–Љ–Є –Њ–≥–Њ–≤–Њ—А–Ї–∞–Љ–Є —Д–Њ—А–Љ—Г–ї–∞ –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ (3.1) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і 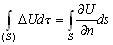 , –≥–і–µ
, –≥–і–µ 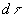 - —Н–ї–µ–Љ–µ–љ—В –Њ–±—КвХ¶–Љ–∞,
- —Н–ї–µ–Љ–µ–љ—В –Њ–±—КвХ¶–Љ–∞, 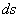 - —Н–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ –±—Г–Ї–≤–Њ–є n –Њ–±–Њ–Ј–љ–∞—З–µ–љ–∞ –≤–љ–µ—И–љ—П—П –љ–Њ—А–Љ–∞–ї—М.
- —Н–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ –±—Г–Ї–≤–Њ–є n –Њ–±–Њ–Ј–љ–∞—З–µ–љ–∞ –≤–љ–µ—И–љ—П—П –љ–Њ—А–Љ–∞–ї—М.
–Я–µ—А–≤–∞—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞
–Т–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ –Њ–њ–µ—А–∞—В–Њ—А–∞
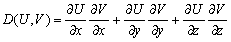 (3.2)
(3.2)
—В–Њ–≥–і–∞ –њ–µ—А–≤–∞—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ –њ—А–Є–Љ–µ—В –≤–Є–і
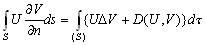 (3.3)
(3.3)
–Ш–љ—В–µ–≥—А–∞–ї –њ–Њ –Њ–±—КвХ¶–Љ—Г –Њ—В —Д—Г–љ–Ї—Ж–Є–Є
D(U,U) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ –Ф–Є—А–Є—Е–ї–µ:
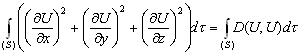 (3.4)
(3.4)
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –≤ —Д–Њ—А–Љ—Г–ї–µ –У—А–Є–љ–∞ —Д—Г–љ–Ї—Ж–Є–Є
U –Є V –Љ–Њ–ґ–љ–Њ –Љ–µ–љ—П—В—М –Љ–µ—Б—В–∞–Љ–Є, —В–Њ –µ—Б—В—М –≤–Љ–µ—Б—В–Њ (3.3) –Љ–Њ–ґ–љ–Њ –љ–∞–њ–Є—Б–∞—В—М
 (3.5)
(3.5)
–Т—В–Њ—А–∞—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞
–Т—Л—З–Є—В–∞—П –ї–µ–≤—Л–µ –Є –њ—А–∞–≤—Л–µ —З–∞—Б—В–Є —Д–Њ—А–Љ—Г–ї (3.3) –Є (3.5), –њ–Њ–ї—Г—З–Є–Љ –≤—В–Њ—А—Г—О —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞
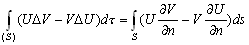 (3.6)
(3.6)
–Ґ—А–µ—В—М—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–∞—Б—В–љ—Л–є —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞
U=1/r, –≥–і–µ r вИЪ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П —В–Њ—З–Ї–∞–Љ–Є P(x,y,z) –Є Q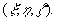 –Я–µ—А–≤–∞—П —В–Њ—З–Ї–∞ –Є–Љ–µ–µ—В —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, –∞ –≤—В–Њ—А–∞—П - –њ—А–Є–љ–∞–і–ї–µ–ґ–Є—В —В–µ–ї—Г –Є –Є–Љ–µ–µ—В —В–µ–Ї—Г—Й–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—Й–Є–µ —Н–ї–µ–Љ–µ–љ—В—Г –Њ–±—КвХ¶–Љ–∞. –Ґ–Њ–≥–і–∞
–Я–µ—А–≤–∞—П —В–Њ—З–Ї–∞ –Є–Љ–µ–µ—В —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, –∞ –≤—В–Њ—А–∞—П - –њ—А–Є–љ–∞–і–ї–µ–ґ–Є—В —В–µ–ї—Г –Є –Є–Љ–µ–µ—В —В–µ–Ї—Г—Й–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—Й–Є–µ —Н–ї–µ–Љ–µ–љ—В—Г –Њ–±—КвХ¶–Љ–∞. –Ґ–Њ–≥–і–∞
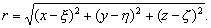
–Э–µ—В—А—Г–і–љ–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ –і–ї—П
r¹
0, –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ D
(1/r)=0. –Ш–Љ–µ–µ–Љ
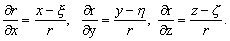
–Я—А–Њ–і–µ–ї–∞–µ–Љ —Б–ї–µ–і—Г—О—Й–Є–µ –≤—Л–Ї–ї–∞–і–Ї–Є
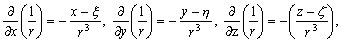
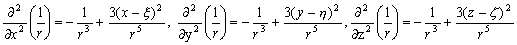 ,
,
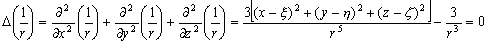 .
.
–Ю–±—А–∞—В–Є–Љ—Б—П —Б–љ–Њ–≤–∞ –Ї –≤—В–Њ—А–Њ–є —Д–Њ—А–Љ—Г–ї–µ –У—А–Є–љ–∞. –Я–µ—А–µ–њ–Є—И–µ–Љ –µвХ¶ –і–ї—П —Б–ї—Г—З–∞—П, –Ї–Њ–≥–і–∞
U=1/r. –Т–Њ–Ј–Љ–Њ–ґ–љ—Л —В—А–Є –≤–∞—А–Є–∞–љ—В–∞, –Ї–Њ–≥–і–∞ —В–Њ—З–Ї–∞ –† –ї–µ–ґ–Є—В –≤–љ–µ —В–µ–ї–∞, –≤–љ—Г—В—А–Є –µ–≥–Њ –Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –Ї–Њ—В–Њ—А–Њ–µ –Њ–≥—А–∞–љ–Є—З–Є–≤–∞–µ—В —Н—В–Њ —В–µ–ї–Њ.
- –Ґ–Њ—З–Ї–∞ –† вИЪ –≤–љ–µ—И–љ—П—П
. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –≤–Њ –≤—БвХ¶–Љ –≤–љ—Г—В—А–µ–љ–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —В–µ–ї–∞, –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –≤–µ–івХ¶—В—Б—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ, —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А r –љ–µ –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –љ—Г–ї—М –Є D
(1/r)= 0. –Т—В–Њ—А–∞—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ (3.6) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
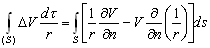 . (3.7)
. (3.7)
–Ь—Л –њ–Њ–ї—Г—З–Є–ї–Є —В—А–µ—В—М—О —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞ –і–ї—П –≤–љ–µ—И–љ–µ–є —В–Њ—З–Ї–Є.
–† - –≤–љ—Г—В—А–µ–љ–љ—П—П. –Т –Њ–і–љ–Њ–є —В–Њ—З–Ї–µ –≤–љ—Г—В—А–µ–љ–љ–µ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –љ—Г–ї—М –Є —Д—Г–љ–Ї—Ж–Є—П 1/r –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М. –Ю–њ–Є—И–µ–Љ –≤–Њ–Ї—А—Г–≥ —Н—В–Њ–є —В–Њ—З–Ї–Є —Б—Д–µ—А—Г s
—Б –Љ–∞–ї—Л–Љ —А–∞–і–Є—Г—Б–Њ–Љ. –Ш–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –њ–Њ —В–µ–ї—Г, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О S, –Љ–Њ–ґ–љ–Њ —А–∞–Ј–±–Є—В—М –љ–∞ –і–≤–∞ —Н—В–∞–њ–∞: –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—О –њ–Њ –≤—Б–µ–Љ —В–Њ—З–Ї–∞–Љ —В–µ–ї–∞, –Є—Б–Ї–ї—О—З–∞—П –Љ–∞–ї—Г—О —Б—Д–µ—А—Г, —Б–Њ–і–µ—А–ґ–∞—Й—Г—О —В–Њ—З–Ї—Г –†, –Є –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –њ–Њ –Љ–∞–ї–Њ–Љ—Г —И–∞—А—Г, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ—Г –Љ–∞–ї–Њ–є —Б—Д–µ—А–Њ–є s
:
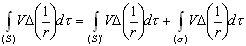 ,
,
–≥–і–µ
(S)¢
- —В–µ–ї–Њ —Б –≤—Л–Ї–Њ–ї–Њ—В–Њ–є —В–Њ—З–Ї–Њ–є –†. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г r¹
0 –≤–Њ –≤—БвХ¶–Љ –≤–љ—Г—В—А–µ–љ–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ (S)¢
, —В–Њ –њ–µ—А–≤–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї—Л –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –љ—Г–ї—М, —В–∞–Ї –Ї–∞–Ї D
(1/r) =0. –Ч–∞–є–ЉвХ¶–Љ—Б—П –≤—В–Њ—А—Л–Љ —Б–ї–∞–≥–∞–µ–Љ—Л–Љ. –С—Г–і–µ–Љ —Б—З–Є—В–∞—В—М, —З—В–Њ —А–∞–і–Є—Г—Б –Љ–∞–ї–Њ–є —Б—Д–µ—А—Л s
–љ–∞—Б—В–Њ–ї—М–Ї–Њ –Љ–∞–ї, —З—В–Њ —Д—Г–љ–Ї—Ж–Є—О V –≤–љ—Г—В—А–Є —Н—В–Њ–є —Б—Д–µ—А—Л - –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ґ–Њ–≥–і–∞
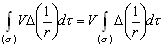
–Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ, –≤ –Ї–Њ—В–Њ—А–Њ–є –њ–Њ–ї–Њ–ґ–Є–Љ
U=1/r , —В–Њ–≥–і–∞ –≤–Љ–µ—Б—В–Њ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –њ–Њ –Њ–±—КвХ¶–Љ—Г –±—Г–і–µ–Љ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞—В—М –њ–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Љ–∞–ї–Њ–є —Б—Д–µ—А—Л
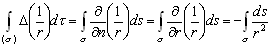 .
.
–Ю—В–љ–Њ—И–µ–љ–Є–µ
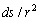 –µ—Б—В—М —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л–є —В–µ–ї–µ—Б–љ—Л–є —Г–≥–Њ–ї
–µ—Б—В—М —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л–є —В–µ–ї–µ—Б–љ—Л–є —Г–≥–Њ–ї  , –њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ вМ†–≤–Є–і–µ–љвЦ† –Є–Ј —В–Њ—З–Ї–Є –† —Н–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ, –µ—Б–ї–Є —В–Њ—З–Ї–∞ –† –љ–∞—Е–Њ–і–Є—В—Б—П –≤–љ—Г—В—А–Є —Н—В–Њ–є —Б—Д–µ—А—Л, —В–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л–є –Є–љ—В–µ–≥—А–∞–ї –±—Г–і–µ—В —А–∞–≤–µ–љ –њ–Њ–ї–љ–Њ–Љ—Г —В–µ–ї–µ—Б–љ–Њ–Љ—Г —Г–≥–ї—Г, –њ–Њ –Ї–Њ—В–Њ—А—Л–Љ –≤–Є–і–љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Б—Д–µ—А—Л –Є–Ј–љ—Г—В—А–Є. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–љ —А–∞–≤–µ–љ 4p
, —В–Њ –µ—Б—В—М
, –њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ вМ†–≤–Є–і–µ–љвЦ† –Є–Ј —В–Њ—З–Ї–Є –† —Н–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ, –µ—Б–ї–Є —В–Њ—З–Ї–∞ –† –љ–∞—Е–Њ–і–Є—В—Б—П –≤–љ—Г—В—А–Є —Н—В–Њ–є —Б—Д–µ—А—Л, —В–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л–є –Є–љ—В–µ–≥—А–∞–ї –±—Г–і–µ—В —А–∞–≤–µ–љ –њ–Њ–ї–љ–Њ–Љ—Г —В–µ–ї–µ—Б–љ–Њ–Љ—Г —Г–≥–ї—Г, –њ–Њ –Ї–Њ—В–Њ—А—Л–Љ –≤–Є–і–љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Б—Д–µ—А—Л –Є–Ј–љ—Г—В—А–Є. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–љ —А–∞–≤–µ–љ 4p
, —В–Њ –µ—Б—В—М
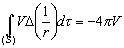
–Я–µ—А–µ–њ–Є—И–µ–Љ —Д–Њ—А–Љ—Г–ї—Г ( 3.6) –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ
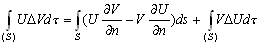 .
.
–Т —Б–ї—Г—З–∞–µ
U=1/r, –і–ї—П –≤–љ–µ—И–љ–µ–є —В–Њ—З–Ї–Є –њ–Њ–ї—Г—З–Є–Љ
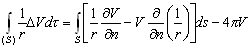 (3.8)
(3.8)
–Ґ–Њ—З–Ї–∞ –† –ї–µ–ґ–Є—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ґ—А–µ—В–Є–є —Б–ї—Г—З–∞–є вИЪ —Н—В–Њ –Ї–Њ–≥–і–∞ —В–Њ—З–Ї–∞ –† –љ–µ —П–≤–ї—П–µ—В—Б—П –љ–Є –≤–љ—Г—В—А–µ–љ–љ–µ–є –љ–Є –≤–љ–µ—И–љ–µ–є: –Њ–љ–∞ –ї–µ–ґ–Є—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —В–µ–ї–∞. –Ь–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ
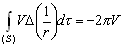 ,
,
–њ–Њ—Н—В–Њ–Љ—Г —В—А–µ—В—М—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
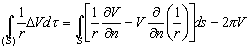 (3.9)
(3.9)
–§–Њ—А–Љ—Г–ї—Л (3.7),(3.8) –Є (3.9) –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –Њ–і–љ–Њ–є —Д–Њ—А–Љ—Г–ї–Њ–є
 (3.10)
(3.10)
–У–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
–У–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В
x, y, z –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Д—Г–љ–Ї—Ж–Є—П, –љ–µ–њ—А–µ—А—Л–≤–љ–∞—П –≤–Љ–µ—Б—В–µ —Б–Њ —Б–≤–Њ–Є–Љ–Є –њ–µ—А–≤—Л–Љ–Є –Є –≤—В–Њ—А—Л–Љ–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–Љ–Є –≤ –љ–µ–Ї–Њ—В–Њ—А–Њ–є –Њ–±–ї–∞—Б—В–Є (S), —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–∞—П –≤–Њ –≤—Б–µ—Е —В–Њ—З–Ї–∞—Е —Н—В–Њ–є –Њ–±–ї–∞—Б—В–Є —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞ D
V=0.
–°–≤–Њ–є—Б—В–≤–∞ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є
.
–Ы–Є–љ–µ–є–љ–∞—П –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –і–≤—Г—Е –Є –±–Њ–ї–µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –µ—Б—В—М —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П.
–Я—Г—Б—В—М
U(x,y,z) –Є V(x,y,z) - –і–≤–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є, —В–Њ –µ—Б—В—М D
U(x,y,z)=0 –Є D
V(x,y,z)=0. –Т–Њ–Ј—М–ЉвХ¶–Љ –Є—Е –ї–Є–љ–µ–є–љ—Г—О –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—О W(x,y,z)=AU(x,y,z)+BV(x,y,z). –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ D
W=AD
U+BD
V. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г D
U=0, D
V=0, —В–Њ –Є D
W=0 , —З—В–Њ –Є –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –љ–∞—И–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ.
–Х—Б–ї–Є V - –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, —В–Њ –≤—Б–µ –µвХ¶ —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є.
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ –Њ—Б–љ–Њ–≤–∞–љ–Њ –љ–∞ –≤–Ј–∞–Є–Љ–љ–Њ–є –њ–µ—А–µ—Б—В–∞–≤–Є–Љ–Њ—Б—В–Є –Њ–њ–µ—А–∞—В–Њ—А–∞ –Ы–∞–њ–ї–∞—Б–∞ D
–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е. –Я—Г—Б—В—М
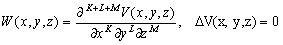 ,
,
—В–Њ–≥–і–∞  –Ы–Є–љ–µ–є–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В (–њ–Њ–≤–Њ—А–Њ—В –Њ—Б–µ–є, –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Љ–∞—Б—И—В–∞–±–∞) –љ–µ –љ–∞—А—Г—И–∞–µ—В —Б–≤–Њ–є—Б—В–≤–Њ –≥–∞—А–Љ–Њ–љ–Є—З–љ–Њ—Б—В–Є.
–Ы–Є–љ–µ–є–љ–Њ–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В (–њ–Њ–≤–Њ—А–Њ—В –Њ—Б–µ–є, –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Љ–∞—Б—И—В–∞–±–∞) –љ–µ –љ–∞—А—Г—И–∞–µ—В —Б–≤–Њ–є—Б—В–≤–Њ –≥–∞—А–Љ–Њ–љ–Є—З–љ–Њ—Б—В–Є.
–Я—Г—Б—В—М
U(x,y,z) вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П. –Т–≤–µ–і–µ–Љ –љ–Њ–≤—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л
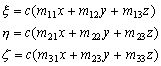
–Т –Љ–∞—В—А–Є—З–љ–Њ–Љ –≤–Є–і–µ –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–µ —А–∞–≤–µ–љ—Б—В–≤–Њ –≤—Л–≥–ї—П–і–Є—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
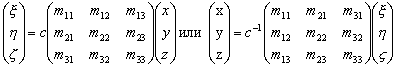
–Я–Њ–і—Б—В–∞–≤–Є–Љ –≤ —Д—Г–љ–Ї—Ж–Є—О
U(x,y,z) –ї–Є–љ–µ–є–љ—Л–µ –≤—Л—А–∞–ґ–µ–љ–Є—П –і–ї—П x
, h
, V
, –і–ї—П —З–µ–≥–Њ –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –≤—В–Њ—А—Л–Љ –Є–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е –≤—Л—И–µ —А–∞–≤–µ–љ—Б—В–≤, –њ–Њ–ї—Г—З–Є–Љ V(x
h
V
). –Ф–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ –µ—Б–ї–Є U(x,y,z) —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, —В–Њ –Є V(
x
h
V
)
—П–≤–ї—П–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є.
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
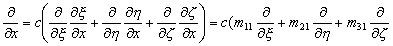 )
)
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ
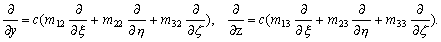
–Ч–∞–њ–Є—И–µ–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —А–∞–≤–µ–љ—Б—В–≤–∞ –≤ –Љ–∞—В—А–Є—З–љ–Њ–є —Д–Њ—А–Љ–µ
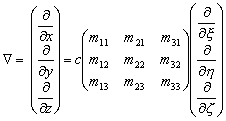
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –µ—Б—В—М –Ї–≤–∞–і—А–∞—В –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –Њ–њ–µ—А–∞—В–Њ—А–∞ –љ–∞–±–ї–∞, —В–Њ
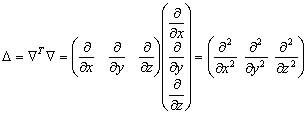 ,
,
–Т –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –±—Г–і–µ–Љ –Є–Љ–µ—В—М
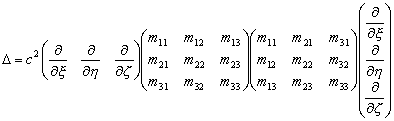
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Љ–∞—В—А–Є—Ж—Л –љ–∞–њ—А–∞–≤–ї—П—О—Й–Є—Е –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ —П–≤–ї—П—О—В—Б—П –Њ—А—В–Њ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є, –Є—Е –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П —А–∞–≤–љ—Л –µ–і–Є–љ–Є—З–љ–Њ–є –Љ–∞—В—А–Є—Ж–µ –Є –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
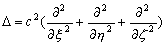 .
.
–Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ —П–≤–ї—П–µ—В—Б—П –Є–љ–≤–∞—А–Є–∞–љ—В–Њ–Љ –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї –њ–Њ–≤–Њ—А–Њ—В—Г –Њ—Б–µ–є, –∞ –њ—А–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–Є –Љ–∞—Б—И—В–∞–±–∞ –Љ–љ–Њ–ґ–Є—В–µ–ї–µ–Љ —Б –Є–Ј–Љ–µ–љ—П–µ—В—Б—П –љ–∞ –Љ–љ–Њ–ґ–Є—В–µ–ї—М
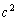 . –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –µ—Б–ї–Є D
U(x,y,z) =0, —В–Њ
. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –µ—Б–ї–Є D
U(x,y,z) =0, —В–Њ 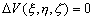 .
.
–Ґ–µ–Њ—А–µ–Љ—Л –Њ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є—П—Е
–Ґ–µ–Њ—А–µ–Љ–∞ –У–∞—Г—Б—Б–∞. –Я–Њ—В–Њ–Ї –≥—А–∞–і–Є–µ–љ—В–∞ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —З–µ—А–µ–Ј –Ј–∞–Љ–Ї–љ—Г—В—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —А–∞–≤–µ–љ –љ—Г–ї—О. –Я–Њ—В–Њ–Ї–Њ–Љ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Є–љ—В–µ–≥—А–∞–ї –њ–Њ –Ј–∞–і–∞–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ—В –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є.
–Я—Г—Б—В—М
V(x,y,z) вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П. –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ –Ј–∞–і–∞–љ–∞ –Ј–∞–Љ–Ї–љ—Г—В–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М S, –Њ–≥—А–∞–љ–Є—З–Є–≤–∞—О—Й–∞—П –Њ–±–ї–∞—Б—В—М, –≤–љ—Г—В—А–Є –Ї–Њ—В–Њ—А–Њ–є —Н—В–∞ —Д—Г–љ–Ї—Ж–Є—П вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П. –Ґ–Њ–≥–і–∞, –Є—Б–њ–Њ–ї—М–Ј—Г—П —Д–Њ—А–Љ—Г–ї—Г –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ (3.1), –њ–Њ–ї—Г—З–Є–Љ
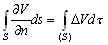
–Э–Њ —В–∞–Ї –Ї–∞–Ї —Д—Г–љ–Ї—Ж–Є—П
V –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, —В–Њ D
V=0, –њ–Њ—Н—В–Њ–Љ—Г 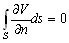
–Т —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞
V(x,y,z) вИЪ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П, —В–Њ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Я—Г–∞—Б—Б–Њ–љ–∞ 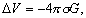 –≥–і–µ s
- –њ–ї–Њ—В–љ–Њ—Б—В—М –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є—Е –Љ–∞—Б—Б. –Ґ–Њ–≥–і–∞ —Д–Њ—А–Љ—Г–ї–∞ (3.1) –њ—А–Є–≤–Њ–і–Є—В –Ї —Д–Њ—А–Љ—Г–ї–µ –У–∞—Г—Б—Б–∞.
–≥–і–µ s
- –њ–ї–Њ—В–љ–Њ—Б—В—М –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є—Е –Љ–∞—Б—Б. –Ґ–Њ–≥–і–∞ —Д–Њ—А–Љ—Г–ї–∞ (3.1) –њ—А–Є–≤–Њ–і–Є—В –Ї —Д–Њ—А–Љ—Г–ї–µ –У–∞—Г—Б—Б–∞.
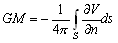
(3.11)
–У–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –≤ –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –Њ–±–ї–∞—Б—В–Є D –љ–µ –Є–Љ–µ–µ—В –љ–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞, –љ–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ –Њ–±—А–∞—В–љ–Њ–µ: –≤–љ—Г—В—А–Є –Њ–±–ї–∞—Б—В–Є
D —Б—Г—Й–µ—Б—В–≤—Г–µ—В —В–Њ—З–Ї–∞ –†, –≤ –Ї–Њ—В–Њ—А–Њ–є –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –Є–Љ–µ–µ—В –Љ–∞–Ї—Б–Є–Љ—Г–Љ. –Т –Љ–∞–ї–Њ–є –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —Н—В–Њ–є —В–Њ—З–Ї–Є –љ–∞ —Б—Д–µ—А–µ S
–љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П —Д—Г–љ–Ї—Ж–Є–Є V –±—Г–і–µ—В –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–Њ–є, —В–Њ–≥–і–∞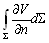 <
0, —З—В–Њ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В —В–µ–Њ—А–µ–Љ–µ –У–∞—Г—Б—Б–∞.
–Я–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤–љ–µ –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є—Е –Љ–∞—Б—Б –љ–µ –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М –љ–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞, –љ–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞; –≤–љ—Г—В—А–Є —Н—В–Њ–є –Њ–±–ї–∞—Б—В–Є –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М —В–Њ–ї—М–Ї–Њ –Љ–∞–Ї—Б–Є–Љ—Г–Љ.
<
0, —З—В–Њ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В —В–µ–Њ—А–µ–Љ–µ –У–∞—Г—Б—Б–∞.
–Я–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤–љ–µ –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–Є—Е –Љ–∞—Б—Б –љ–µ –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М –љ–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞, –љ–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞; –≤–љ—Г—В—А–Є —Н—В–Њ–є –Њ–±–ї–∞—Б—В–Є –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М —В–Њ–ї—М–Ї–Њ –Љ–∞–Ї—Б–Є–Љ—Г–Љ.
–Ы—О–±–∞—П –Њ–±–ї–∞—Б—В—М –≤–љ–µ –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ —В–µ–ї–∞ –µ—Б—В—М –Њ–±–ї–∞—Б—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, –≤–љ—Г—В—А–Є –Ї–Њ—В–Њ—А–Њ–є, —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ 2, –љ–µ –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М –љ–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞, –љ–Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞. –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ –Њ–±—А–∞—В–љ–Њ–µ: –≤–љ—Г—В—А–Є –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ —В–µ–ї–∞ —Б—Г—Й–µ—Б—В–≤—Г–µ—В —В–Њ—З–Ї–∞ –†, –≤ –Ї–Њ—В–Њ—А–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –і–Њ—Б—В–Є–≥–∞–µ—В –Љ–Є–љ–Є–Љ—Г–Љ–∞. –Т —Н—В–Њ–є —В–Њ—З–Ї–µ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Я—Г–∞—Б—Б–Њ–љ–∞ D
V(P)= -4p
Gs
<
0. –Я–Њ —Д–Њ—А–Љ—Г–ї–µ –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ –±—Г–і–µ–Љ –Є–Љ–µ—В—М
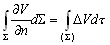 <
0
<
0
M
—Л –њ—А–Є—И–ї–Є –Ї –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—О: –≤—Б–ї–µ–і—Б—В–≤–Є–µ –Љ–Є–љ–Є–Љ—Г–Љ–∞ –≤–љ—Г—В—А–Є –Љ–∞–ї–Њ–є —Б—Д–µ—А—Л, –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н—В–Њ–є —Б—Д–µ—А—Л –±—Г–і–µ—В –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ–є, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Є –њ—А–Є–≤–µ–івХ¶–љ–љ—Л–µ –≤—Л—И–µ –Є–љ—В–µ–≥—А–∞–ї—Л –±—Г–і—Г—В –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л, —З—В–Њ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В —Б–і–µ–ї–∞–љ–љ–Њ–Љ—Г –≤—Л—И–µ –≤—Л–≤–Њ–і—Г. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В–µ–Њ—А–µ–Љ—Г –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М –і–Њ–Ї–∞–Ј–∞–љ–љ–Њ–є.
–Ґ–µ–Њ—А–µ–Љ–∞ –У–∞—Г—Б—Б–∞. –Ч–љ–∞—З–µ–љ–Є–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤ —Ж–µ–љ—В—А–µ —Б—Д–µ—А—Л —А–∞–≤–љ–Њ —Б—А–µ–і–љ–µ–Љ—Г –Є–Ј –Ј–љ–∞—З–µ–љ–Є–є —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є.
–Ю–±—А–∞—В–Є–Љ—Б—П –Ї —В—А–µ—В—М–µ–є —Д–Њ—А–Љ—Г–ї–µ –У—А–Є–љ–∞, –Ї–Њ–≥–і–∞ —В–Њ—З–Ї–∞ –† –≤–љ—Г—В—А–µ–љ–љ—П—П. –Ф–ї—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є D
V=0, –њ–Њ—Н—В–Њ–Љ—Г –љ–∞ —Б—Д–µ—А–µ S
—Д–Њ—А–Љ—Г–ї–∞ (3.8) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
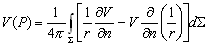 .
.
–Э–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ–Њ —А–∞–і–Є—Г—Б- –≤–µ–Ї—В–Њ—А—Г, –њ–Њ—Н—В–Њ–Љ—Г
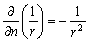 . –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л r=R, –њ–Њ—Н—В–Њ–Љ—Г
. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л r=R, –њ–Њ—Н—В–Њ–Љ—Г  , –љ–Њ —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ –У–∞—Г—Б—Б–∞ –Њ –њ–Њ—В–Њ–Ї–µ –њ–µ—А–≤–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ –≤ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є —А–∞–≤–љ–Њ –љ—Г–ї—О, —В–Њ –µ—Б—В—М
, –љ–Њ —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ –У–∞—Г—Б—Б–∞ –Њ –њ–Њ—В–Њ–Ї–µ –њ–µ—А–≤–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ –≤ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є —А–∞–≤–љ–Њ –љ—Г–ї—О, —В–Њ –µ—Б—В—М
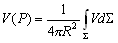 ,
,
—З—В–Њ –Є —В—А–µ–±–Њ–≤–∞–ї–Њ—Б—М –і–Њ–Ї–∞–Ј–∞—В—М.
–®–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є
–®–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є —Б—В–µ–њ–µ–љ–Є
n –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, —П–≤–ї—П—О—Й–∞—П—Б—П –Њ–і–љ–Њ—А–Њ–і–љ—Л–Љ —Б—В–µ–њ–µ–љ–љ—Л–Љ –њ–Њ–ї–Є–љ–Њ–Љ–Њ–Љ –≤–Є–і–∞
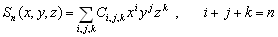
(3.11)
–≥–і–µ
 –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ.
–њ–Њ—Б—В–Њ—П–љ–љ—Л–µ.
–Т–Њ–Ј—М–ЉвХ¶–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В
 (3.12)
(3.12)
–≥–і–µ l
- –і–Њ–ї–≥–Њ—В–∞, q
- –њ–Њ–ї—П—А–љ–Њ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ, r
- —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —В–Њ—З–Ї–Є –†. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
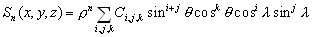
(3.13)
–§—Г–љ–Ї—Ж–Є—П –≤–Є–і–∞
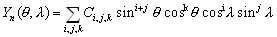 (3.14)
(3.14)
–љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є.
–Ш—В–∞–Ї, —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П —Б—В–µ–њ–µ–љ–Є
n –Є–Љ–µ–µ—В –≤–Є–і
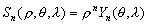 (3.15)
(3.15)
–°—Г—Й–µ—Б—В–≤—Г–µ—В –Є –і—А—Г–≥–Њ–є –Ї–ї–∞—Б—Б —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є, –Ї–Њ—В–Њ—А—Л–є –њ—А–Є–≤–µ–івХ¶–Љ –Ј–і–µ—Б—М –±–µ–Ј –≤—Л–≤–Њ–і–∞
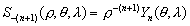 , (3.16)
, (3.16)
–≥–і–µ
 - —В–∞ –ґ–µ —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Ї–Њ—В–Њ—А–∞—П –≤—Е–Њ–і–Є—В –Є –≤ —Д–Њ—А–Љ—Г–ї—Г (3.15).
- —В–∞ –ґ–µ —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Ї–Њ—В–Њ—А–∞—П –≤—Е–Њ–і–Є—В –Є –≤ —Д–Њ—А–Љ—Г–ї—Г (3.15).
–І–Є—Б–ї–Њ –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —Б—В–µ–њ–µ–љ–Є
n —А–∞–≤–љ–Њ 2n+1. –£–±–µ–і–Є–Љ—Б—П –≤ —Н—В–Њ–Љ –љ–∞ –њ—А–Є –Љ–µ—А–µ —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —В—А–µ—В—М–µ–є —Б—В–µ–њ–µ–љ–Є:
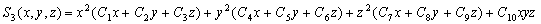 .
.
–Т—Б–µ–≥–Њ –Њ–і–љ–Њ—А–Њ–і–љ—Л–є –њ–Њ–ї–Є–љ–Њ–Љ —В—А–µ—В—М–µ–є —Б—В–µ–њ–µ–љ–Є –Є–Љ–µ–µ—В 10 –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е. –Ю–і–љ–∞–Ї–Њ –љ–µ –≤—Б–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л
. –®–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –њ–Њ–і—З–Є–љ—П—О—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞. –Т—Л–њ–Њ–ї–љ–Є–≤ –љ–µ–Њ–±—Е–Њ–і–Є–Љ—Л–µ –≤—Л–Ї–ї–∞–і–Ї–Є, –њ–Њ–ї—Г—З–Є–Љ
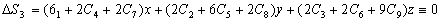
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є–Ј 10 –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е 3 –ї–Є–љ–µ–є–љ–Њ —Б–≤—П–Ј–∞–љ—Л —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –Ы–∞–њ–ї–∞—Б–∞. –Ю—Б—В–∞вХ¶—В—Б—П 10-3=7 –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е.
–Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —И–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞, —В–Њ –µ—Б—В—М
 ,
, 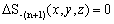 , —В–Њ –і–Њ–ї–ґ–љ—Л –≤—Л–њ–Њ–ї–љ—П—В—М—Б—П –Є —Г—А–∞–≤–љ–µ–љ–Є—П
, —В–Њ –і–Њ–ї–ґ–љ—Л –≤—Л–њ–Њ–ї–љ—П—В—М—Б—П –Є —Г—А–∞–≤–љ–µ–љ–Є—П 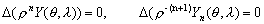 .–Ш–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –µ—Б–ї–Є
.–Ш–Ј –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –µ—Б–ї–Є  - –Њ–±–Њ–±—ЙвХ¶–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, —В–Њ —Н–ї–µ–Љ–µ–љ—В –і—Г–≥–Є –≤ —Н—В–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
- –Њ–±–Њ–±—ЙвХ¶–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, —В–Њ —Н–ї–µ–Љ–µ–љ—В –і—Г–≥–Є –≤ —Н—В–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
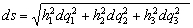 ,
,
–≥–і–µ
 вИЪ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ы–∞–Љ–µ:
вИЪ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ы–∞–Љ–µ:
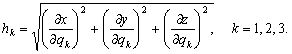
–Ґ–µ–њ–µ—А—М –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ (–±–µ–Ј –≤—Л–≤–Њ–і–∞)
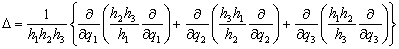 (3.17)
(3.17)
–Ю–њ—А–µ–і–µ–ї–Є–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ы–∞–Љ–µ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В. –Т –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ
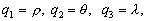 –њ–Њ—Н—В–Њ–Љ—Г
–њ–Њ—Н—В–Њ–Љ—Г

–Ю–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —В–∞–Ї
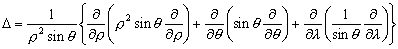 (3.18)
(3.18)
–Я—А–Є–Љ–µ–љ–Є–Љ —Н—В–Њ—В –Њ–њ–µ—А–∞—В–Њ—А –Ї —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤–Є–і–∞
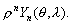 –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —А–∞–≤–µ–љ –љ—Г–ї—О, –њ–Њ—Н—В–Њ–Љ—Г
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –Њ–њ–µ—А–∞—В–Њ—А –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —А–∞–≤–µ–љ –љ—Г–ї—О, –њ–Њ—Н—В–Њ–Љ—Г
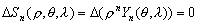

–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –њ–Њ—А—П–і–Ї–∞
n –Є–Љ–µ–µ—В –≤–Є–і
–Є–Љ–µ–µ—В –≤–Є–і
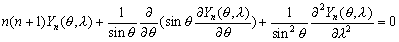 (3.19)
(3.19)

–Я—А–µ–і–ї–∞–≥–∞–µ–Љ —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ —Г–±–µ–і–Є—В—М—Б—П –≤ —В–Њ–Љ, –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П —Д—Г–љ–Ї—Ж–Є–Є 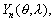 –≤—Е–Њ–і—П—Й—Г—О –≤ —И–∞—А–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞
–≤—Е–Њ–і—П—Й—Г—О –≤ —И–∞—А–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞  —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ (3.19).
—Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ (3.19).
–Ш–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П
–Ч–∞–Љ–µ–љ–Є–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Г—О
cosq
–љ–∞ t, —В–Њ–≥–і–∞ dt=-sinq
dq
. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
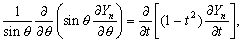
–њ–Њ—Н—В–Њ–Љ—Г –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ (3.19) –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —В–∞–Ї
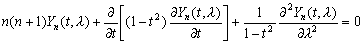 (3,20)
(3,20)
–С—Г–і–µ–Љ –Є—Б–Ї–∞—В—М —А–µ—И–µ–љ–Є–µ —Н—В–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –≤ –≤–Є–і–µ
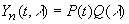 . –Я–Њ–і—Б—В–∞–≤–Є–≤ —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ, –±—Г–і–µ–Љ –Є–Љ–µ—В—М
. –Я–Њ–і—Б—В–∞–≤–Є–≤ —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ, –±—Г–і–µ–Љ –Є–Љ–µ—В—М
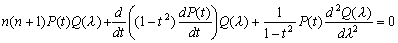
–£–Љ–љ–Њ–ґ–Є–Љ –Ї–∞–ґ–і—Л–є —З–ї–µ–љ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ –≤—Л—А–∞–ґ–µ–љ–Є—П –љ–∞
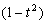 –Є –њ–Њ–і–µ–ї–Є–Љ –љ–∞ P(t)Q(l
), –њ–Њ–ї—Г—З–Є–Љ
–Є –њ–Њ–і–µ–ї–Є–Љ –љ–∞ P(t)Q(l
), –њ–Њ–ї—Г—З–Є–Љ
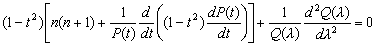
–Т–Є–і–Є–Љ, —З—В–Њ –њ–µ—А–≤—Л–µ –і–≤–∞ —З–ї–µ–љ–∞ –Ј–∞–≤–Є—Б—П—В —В–Њ–ї—М–Ї–Њ –Њ—В
t ,–∞ –њ–Њ—Б–ї–µ–і–љ–Є–є - —В–Њ–ї—М–Ї–Њ –Њ—В l
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Г—А–∞–≤–љ–µ–љ–Є–µ –≤—Л–њ–Њ–ї–љ—П–ї–Њ—Б—М –і–ї—П –ї—О–±—Л—Е t –Є l
, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л —Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є –≤—Л—А–Њ–і–Є–ї–Є—Б—М –≤ –Ї–Њ–љ—Б—В–∞–љ—В—Л. –Э–∞–њ—А–Є–Љ–µ—А, —Г—А–∞–≤–љ–µ–љ–Є–µ –±—Г–і–µ—В –≤—Л–њ–Њ–ї–љ—П—В—М—Б—П, –µ—Б–ї–Є
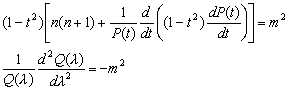 (3.21)
(3.21)
–Т—В–Њ—А–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –µ—Б—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є
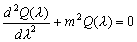 .
.
–Х–≥–Њ —А–µ—И–µ–љ–Є–µ –і–ї—П –ї—О–±—Л—Е –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є
m –Є–Љ–µ–µ—В –≤–Є–і
Q(l
)=A cosml
+B sinml
,
–≥–і–µ –Р –Є –Т - –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П
.
–†–µ—И–µ–љ–Є–µ –њ–µ—А–≤–Њ–≥–Њ –Є–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е –≤—Л—И–µ —Г—А–∞–≤–љ–µ–љ–Є–є, –Ј–∞–≤–Є—Б–Є—В –Ї–∞–Ї –Њ—В –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є
m, —В–∞–Ї –Є –Њ—В –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є n. –Ю–±–Њ–Ј–љ–∞—З–Є–≤ —А–µ—И–µ–љ–Є–µ —З–µ—А–µ–Ј 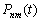 , –њ–Њ–ї—Г—З–Є–Љ
, –њ–Њ–ї—Г—З–Є–Љ
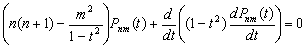 (3.22)
(3.22)
–§—Г–љ–Ї—Ж–Є—П
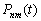 –њ—А–Є —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ –њ—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ–Њ–є (–∞—Б—Б–Њ—Ж–Є–∞—В–Є–≤–љ–Њ–є) —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞. –Т —Б–ї—Г—З–∞–µ m=0, —Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є —Б—В–∞–љ–Њ–≤—П—В—Б—П —Б—В–µ–њ–µ–љ–љ—Л–Љ–Є –њ–Њ–ї–Є–љ–Њ–Љ–∞–Љ–Є, –Ї–Њ—В–Њ—А—Л–µ –љ–∞–Ј—Л–≤–∞—О—В—Б—П –њ–Њ–ї–Є–љ–Њ–Љ–∞–Љ–Є –Ы–µ–ґ–∞–љ–і—А–∞. –Я–Њ–ї–∞–≥–∞—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (3.22) m=0,. –њ–Њ–ї—Г—З–Є–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞
–њ—А–Є —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е m –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ –њ—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ–Њ–є (–∞—Б—Б–Њ—Ж–Є–∞—В–Є–≤–љ–Њ–є) —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞. –Т —Б–ї—Г—З–∞–µ m=0, —Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є —Б—В–∞–љ–Њ–≤—П—В—Б—П —Б—В–µ–њ–µ–љ–љ—Л–Љ–Є –њ–Њ–ї–Є–љ–Њ–Љ–∞–Љ–Є, –Ї–Њ—В–Њ—А—Л–µ –љ–∞–Ј—Л–≤–∞—О—В—Б—П –њ–Њ–ї–Є–љ–Њ–Љ–∞–Љ–Є –Ы–µ–ґ–∞–љ–і—А–∞. –Я–Њ–ї–∞–≥–∞—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (3.22) m=0,. –њ–Њ–ї—Г—З–Є–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞
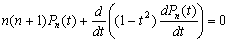 (3.23)
(3.23)
–Т —В–µ–Њ—А–Є–Є —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є —Б–≤–Њ–є—Б—В–≤–∞ —Д—Г–љ–Ї—Ж–Є–є –Є –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Е–Њ—А–Њ—И–Њ –Є–Ј—Г—З–µ–љ—Л. –Я—А–Є–≤–µ–і–µ–Љ –ї–Є—И—М –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–µ–і–µ–љ–Є—П(–±–µ–Ј –≤—Л–≤–Њ–і–∞), –Ї–Њ—В–Њ—А—Л–µ –Љ–Њ–≥—Г—В –њ—А–Є–≥–Њ–і–Є—В—М—Б—П –≤ –љ–∞—И–µ–Љ –Ї—Г—А—Б–µ. –Я—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞ –Є –њ–Њ–ї–Є–љ–Њ–Љ—Л –Ы–µ–ґ–∞–љ–і—А–∞ —Б–≤—П–Ј–∞–љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ
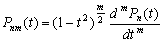 (3.24)
(3.24)
–Я–Њ–і–≤–Њ–і—П –Є—В–Њ–≥ —Б–Ї–∞–Ј–∞–љ–љ–Њ–Љ—Г, –≤—Л–њ–Є—И–µ–Љ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ—Л–є –≤–Є–і —А–µ—И–µ–љ–Є—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є
 (3.25)
(3.25)
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –њ–Њ—А—П–і–Њ–Ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є
m –≤ (3.24) –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –±–Њ–ї—М—И–µ —Б—В–µ–њ–µ–љ–Є n –њ–Њ–ї–Є–љ–Њ–Љ–∞ –Ы–µ–ґ–∞–љ–і—А–∞. –Я–Њ —Н—В–Њ–є –њ—А–Є—З–Є–љ–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ n –Є m –љ–∞–Ј—Л–≤–∞—О—В —Б—В–µ–њ–µ–љ—М—О –Є –њ–Њ—А—П–і–Ї–Њ–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є.
–Ы–µ–Ї—Ж–Є—П 4
–Я–Њ–ї–Є–љ–Њ–Љ—Л –Ы–µ–ґ–∞–љ–і—А–∞ –Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є.–Ю—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В—М —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є. –Э–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є–µ. –†—П–і –Ы–∞–њ–ї–∞—Б–∞. –Р–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–є, –Ј–∞–і–∞–љ–љ—Л—Е –љ–∞ —Б—Д–µ—А–µ. –§—Г–љ–Ї—Ж–Є–Є –Ы–∞–њ–ї–∞—Б–∞.
–°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
–Я–Њ–ї–Є–љ–Њ–Љ—Л –Ы–µ–ґ–∞–љ–і—А–∞ –Є –Є—Е —Б–≤–Њ–є—Б—В–≤–∞
–Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є, –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –њ–Њ–ї–Є–љ–Њ–Љ–∞–Љ–Є –Є —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –Ы–µ–ґ–∞–љ–і—А–∞, –Ї–Њ—В–Њ—А—Л–µ –≤—Е–Њ–і—П—В –≤ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є–є –≤–Є–і —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є. –Ф–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є–є –Ј–љ–∞—З–µ–љ–Є–є –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤, –Є –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П —А—П–і–∞ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є—Е –≤—Л–Ї–ї–∞–і–Њ–Ї –≤–µ—Б—М–Љ–∞ –њ–Њ–ї–µ–Ј–љ—Л–Љ–Є —П–≤–ї—П—О—В—Б—П –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤, –љ–∞ –Ї–Њ—В–Њ—А—Л—Е –Љ—Л –Ј–і–µ—Б—М –Њ—Б—В–∞–љ–Њ–≤–Є–Љ—Б—П.
–†–µ–Ї—Г—А—А–µ–љ—В–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ–ї–Є–љ–Њ–Љ
n+1 —Б—В–µ–њ–µ–љ–Є, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ—Л –Ј–љ–∞—З–µ–љ–Є—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ n –Є n-1 —Б—В–µ–њ–µ–љ–µ–є
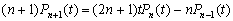 (4.1)
(4.1)
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞
–Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –≤ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П —А—П–і–Њ–Љ –њ–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ. –Ю–љ–∞ –Є–Љ–µ–µ—В –≤–Є–і
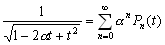 (4.2)
(4.2)
–Я–Њ—Б—В—А>–Ю—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В—М–µ–ґ–∞–љ–і—А–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є
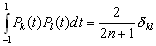 (4.3)
(4.3)
–≥–і–µ
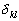 - —Б–Є–Љ–≤–Њ–ї –Ъ—А–Њ–љ–µ–Ї–µ—А–∞. –Я—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞ —В–∞–Ї–ґ–µ –Њ–±–ї–∞–і–∞—О—В —Б–≤–Њimes New Roman" –є—Б—В–≤–Њ–Љ –Њ—А—В–Њ–≥–Њ–љ–∞–ї–Є —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ
- —Б–Є–Љ–≤–Њ–ї –Ъ—А–Њ–љ–µ–Ї–µ—А–∞. –Я—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞ —В–∞–Ї–ґ–µ –Њ–±–ї–∞–і–∞—О—В —Б–≤–Њimes New Roman" –є—Б—В–≤–Њ–Љ –Њ—А—В–Њ–≥–Њ–љ–∞–ї–Є —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ
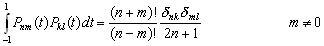 (4.4)
(4.4)
–°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —В–∞–Ї–ґ–µ –Њ–±—А–∞–Ј—Г—О—В –Ї–ї–∞—Б—Б –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є. –Ф–Њ–Ї–∞–ґ–µ–Љ —Б–≤–Њ–є—Б—В–≤–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є. –Т–Њ–Ј—М–ЉвХ¶–Љ –і–≤–µ —И–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞
:  –Є
–Є 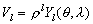 . –Я—А–Є–Љ–µ–љ–Є–Љ –Ї –љ–Є–Љ –≤—В–Њ—А—Г—О —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞ –і–ї—П —Б—Д–µ—А—Л. –£—З–Є—В—Л–≤–∞—П, —З—В–Њ
. –Я—А–Є–Љ–µ–љ–Є–Љ –Ї –љ–Є–Љ –≤—В–Њ—А—Г—О —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞ –і–ї—П —Б—Д–µ—А—Л. –£—З–Є—В—Л–≤–∞—П, —З—В–Њ 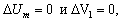 —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
—Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
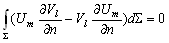 (4.5)
(4.5)
–Ф–ї—П —Б—Д–µ—А—Л –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ –љ–Њ—А–Љ–∞–ї–Є —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ–Њ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А—Г r
, –њ–Њ—Н—В–Њ–Љ—Г
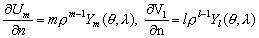
–Я–Њ–і—Б—В–∞–≤–ї—П—П –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –≤—Л—А–∞–ґ–µ–љ–Є—П –≤ —Д–Њ—А–Љ—Г–ї—Г (4.5), –±—Г–і–µ–Љ –Є–Љ–µ—В—М
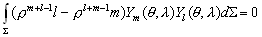
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ
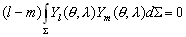 (4.6)
(4.6)
–Я—А–Є
m¹
l –њ—А–Є–≤–µ–івХ¶–љ–љ—Л–є –Є–љ—В–µ–≥—А–∞–ї —А–∞–≤–µ–љ –љ—Г–ї—О, —З—В–Њ —Г–Ї–∞–Ј—Л–≤–∞–µ—В –љ–∞ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В—М —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є.
–Т–µ—А–љвХ¶–Љ—Б—П —В–µ–њ–µ—А—М –Ї —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ —Б—В–µ–њ–µ–љ–Є
n, –Ј–∞–і–∞–љ–љ–Њ–є –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ
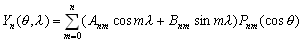 (4.7)
(4.7)
–§—Г–љ–Ї—Ж–Є–Є –≤–Є–і–∞
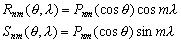 (4.8)
(4.8)
–љ–∞–Ј—Л–≤–∞—О—В—Б—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ–Є –≥–∞—А–Љ–Њ–љ–Є–Ї–∞–Љ–Є. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
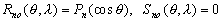 . –Ь–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ
. –Ь–Њ–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ
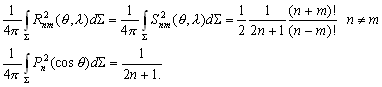 (4.9)
(4.9)
–Т—Б–µ –Њ—Б–љ–Њ–≤–љ—Л–µ –≤—Л–Ї–ї–∞–і–Ї–Є –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –≤ —Г—З–µ–±–љ–Є–Ї–∞—Е –њ–Њ —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ.
–Э–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–µ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
–Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є, —Б—А–µ–і–љ–Є–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–≤–∞–і—А–∞—В–Њ–≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Б–ї–Њ–ґ–љ–Њ –≤—Л—А–∞–ґ–∞—О—В—Б—П —З–µ—А–µ–Ј –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ
m –Є n. –Ю–і–љ–∞–Ї–Њ, –Ї–∞–ґ–і—Г—О –Є–Ј –≥–∞—А–Љ–Њ–љ–Є–Ї –Љ–Њ–ґ–љ–Њ —Г–Љ–љ–Њ–ґ–Є—В—М –љ–∞ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ —В–∞–Ї, —З—В–Њ–±—Л –Є–љ—В–µ–≥—А–∞–ї—Л –≤ —Д–Њ—А–Љ—Г–ї–∞—Е (4.9) –±—Л–ї–Є —А–∞–≤–љ—Л –µ–і–Є–љ–Є—Ж–µ. –≠—В–∞ –Њ–њ–µ—А–∞—Ж–Є—П –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –љ–Њ—А–Љ–Є—А–Њ–≤–Ї–Њ–є. –Ю–±–Њ–Ј–љ–∞—З–∞—П —З–µ—А—В–Њ–є —Б–≤–µ—А—Е—Г –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є, –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
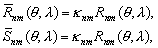
–≥–і–µ
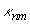 - –љ–Њ—А–Љ–Є—А–Њ–≤–Њ—З–љ—Л–є –Љ–љ–Њ–ґ–Є—В–µ–ї—М. –Т—Л–±–µ—А–µ–Љ –µ–≥–Њ —В–∞–Ї, —З—В–Њ–±—Л –≤—Л–њ–Њ–ї–љ—П–ї–Є—Б—М —А–∞–≤–µ–љ—Б—В–≤–∞
- –љ–Њ—А–Љ–Є—А–Њ–≤–Њ—З–љ—Л–є –Љ–љ–Њ–ґ–Є—В–µ–ї—М. –Т—Л–±–µ—А–µ–Љ –µ–≥–Њ —В–∞–Ї, —З—В–Њ–±—Л –≤—Л–њ–Њ–ї–љ—П–ї–Є—Б—М —А–∞–≤–µ–љ—Б—В–≤–∞
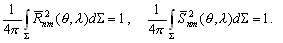 (4.10)
(4.10)
–Ю–±—А–∞—Й–∞—П—Б—М –Ї —Д–Њ—А–Љ—Г–ї–∞–Љ (4.9) –ї–µ–≥–Ї–Њ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ–Љ, —З—В–Њ
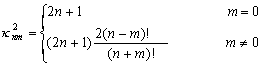
–Я–Њ–ї—Г—З–µ–љ–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
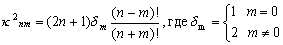 (4.11)
(4.11)
–Ю–њ–µ—А–∞—Ж–Є–Є –љ–Њ—А–Љ–Є—А–Њ–≤–Ї–Є –њ–Њ–і–≤–µ—А–≥–∞—О—В –љ–µ —В–Њ–ї—М–Ї–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є, –љ–Њ –Є –њ–Њ–ї–Є–љ–Њ–Љ—Л –Є —Д—Г–љ–Ї—Ж–Є–Є –Ы–µ–ґ–∞–љ–і—А–∞. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, –µ—Б–ї–Є –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–∞—П —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –Є–Љ–µ–µ—В –≤–Є–і
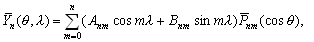 (4.12)
(4.12)
—В–Њ
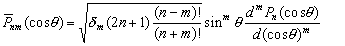
–Р–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—П —Д—Г–љ–Ї—Ж–Є–Є, –Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л, —А—П–і–Њ–Љ –Ы–∞–њ–ї–∞—Б–∞
–°–≤–Њ–є—Б—В–≤–Њ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –і–µ–ї–∞–µ—В –Є—Е –љ–µ–Ј–∞–Љ–µ–љ–Є–Љ—Л–Љ–Є –і–ї—П –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ –њ–Њ–ї—П, —А–µ–ї—М–µ—Д–∞ –Є–ї–Є –і—А—Г–≥–Є—Е –≤–µ–ї–Є—З–Є–љ, –Ј–∞–і–∞–љ–љ—Л—Е –≤ –≤–Є–і–µ –Ї–∞—А—В—Л –љ–∞ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –Є–≥—А–∞—О—В —В—Г –ґ–µ —А–Њ–ї—М, —З—В–Њ –Є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ –і–ї—П –њ—А–Є–±–ї–Є–ґ–µ–љ–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, –Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ –Њ—В—А–µ–Ј–Ї–µ —А—П–і–Њ–Љ –§—Г—А—М–µ. –†—П–і, –Ј–∞–і–∞–љ–љ—Л–є –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї, –Є–љ–Њ–≥–і–∞ –љ–∞–Ј—Л–≤–∞—О—В —А—П–і–Њ–Љ –Ы–∞–њ–ї–∞—Б–∞.
–Я—Г—Б—В—М
 - –Є–Ј–≤–µ—Б—В–љ–∞—П, –Ї—Г—Б–Њ—З–љ–Њ-–љ–µ–њ—А–µ—А—Л–≤–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Ј–∞–і–∞–љ–љ–∞—П –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е. –Р–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—О —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Ј–∞–і–∞–і–Є–Љ –≤ –≤–Є–і–µ –Ї–Њ–љ–µ—З–љ–Њ–≥–Њ —А—П–і–∞, —Б–Њ–і–µ—А–ґ–∞—Й–µ–≥–Њ N —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї
- –Є–Ј–≤–µ—Б—В–љ–∞—П, –Ї—Г—Б–Њ—З–љ–Њ-–љ–µ–њ—А–µ—А—Л–≤–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Ј–∞–і–∞–љ–љ–∞—П –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е. –Р–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—О —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Ј–∞–і–∞–і–Є–Љ –≤ –≤–Є–і–µ –Ї–Њ–љ–µ—З–љ–Њ–≥–Њ —А—П–і–∞, —Б–Њ–і–µ—А–ґ–∞—Й–µ–≥–Њ N —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї
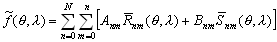 (4.13)
(4.13)
–Ю–њ—А–µ–і–µ–ї–Є–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —Н—В–Њ–≥–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П —В–∞–Ї, —З—В–Њ–±—Л —Д—Г–љ–Ї—Ж–Є—П
 –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞–ї–∞ —Д—Г–љ–Ї—Ж–Є—О
–∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞–ї–∞ —Д—Г–љ–Ї—Ж–Є—О 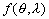 —Б –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ–Љ
—Б –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ–Љ
 (4.14)
(4.14)
–Ф–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤
 –Є
–Є  –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Г—Б–ї–Њ–≤–Є—П–Љ–Є
–≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Г—Б–ї–Њ–≤–Є—П–Љ–Є
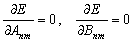 ,
,
–≥–і–µ
m –Є n - –Ј–∞–і–∞–љ–љ—Л–µ —З–Є—Б–ї–∞. –Т—Л–њ–Њ–ї–љ—П—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є–µ, —Б —Г—ЗвХ¶—В–Њ–Љ (4.13), –њ–Њ–ї—Г—З–Є–Љ
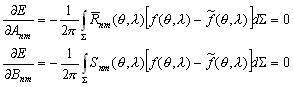 (4.15)
(4.15)
–Т –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –≤—Л—А–∞–ґ–µ–љ–Є—П –љ—Г–ґ–љ–Њ –њ–Њ–і—Б—В–∞–≤–Є—В—М –≤–Љ–µ—Б—В–Њ
 –њ—А–∞–≤—Г—О —З–∞—Б—В—М —Д–Њ—А–Љ—Г–ї—Л (4.13), –Ј–∞–Љ–µ–љ–Є–≤ –≤ –љ–µ–є –Є–љ–і–µ–Ї—Б—Л —Б—Г–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—П m –Є n –љ–∞ k –Є l. –Ь—Л –њ–Њ–ї—Г—З–Є–Љ –Є–љ—В–µ–≥—А–∞–ї—Л –≤–Є–і–∞
–њ—А–∞–≤—Г—О —З–∞—Б—В—М —Д–Њ—А–Љ—Г–ї—Л (4.13), –Ј–∞–Љ–µ–љ–Є–≤ –≤ –љ–µ–є –Є–љ–і–µ–Ї—Б—Л —Б—Г–Љ–Љ–Є—А–Њ–≤–∞–љ–Є—П m –Є n –љ–∞ k –Є l. –Ь—Л –њ–Њ–ї—Г—З–Є–Љ –Є–љ—В–µ–≥—А–∞–ї—Л –≤–Є–і–∞
–Т—Б–ї–µ–і—Б—В–≤–Є–µ –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ–Њ—Б—В–Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї —В–Њ–ї—М–Ї–Њ —В–µ –Є–Ј –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ –Њ—В–ї–Є—З–љ—Л –Њ—В –љ—Г–ї—П, –Ї–Њ—В–Њ—А—Л–µ —Б–Њ–і–µ—А–ґ–∞—В –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Њ–і–љ–Њ–Є–ЉвХ¶–љ–љ—Л—Е –≥–∞—А–Љ–Њ–љ–Є–Ї —Б –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–Љ–Є –Є–љ–і–µ–Ї—Б–∞–Љ–Є. –Т—Л–њ–Њ–ї–љ–Є–≤ –Њ–њ–µ—А–∞—Ж–Є–Є, –њ–Њ–ї—Г—З–Є–Љ
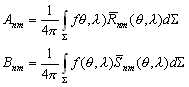 (4.16)
(4.16)
–Ш—В–∞–Ї, –љ–∞–Є–ї—Г—З—И–∞—П —Б—А–µ–і–љ—П—П –Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–∞—П –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—П —Д—Г–љ–Ї—Ж–Є–Є
 –Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ —Б—Д–µ—А–µ, –Љ–љ–Њ–≥–Њ—З–ї–µ–љ–Њ–Љ, —Б–Њ—Б—В–∞–≤–ї–µ–љ–љ—Л–Љ –Є–Ј –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї —Б—В–µ–њ–µ–љ–Є –Є –њ–Њ—А—П–і–Ї–∞ N, –Є–Љ–µ–µ—В –≤–Є–і
–Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ —Б—Д–µ—А–µ, –Љ–љ–Њ–≥–Њ—З–ї–µ–љ–Њ–Љ, —Б–Њ—Б—В–∞–≤–ї–µ–љ–љ—Л–Љ –Є–Ј –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї —Б—В–µ–њ–µ–љ–Є –Є –њ–Њ—А—П–і–Ї–∞ N, –Є–Љ–µ–µ—В –≤–Є–і
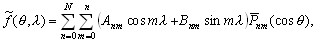 (4.17)
(4.17)
–≥–і–µ
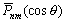 - –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–∞—П –њ—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –Ы–µ–ґ–∞–љ–і—А–∞.
- –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–∞—П –њ—А–Є—Б–Њ–µ–і–Є–љвХ¶–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –Ы–µ–ґ–∞–љ–і—А–∞.
–°–њ–µ—Ж–Є–∞–ї—М–љ–Њ–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –њ–Њ–Ї–∞–Ј–∞–ї–Њ, —З—В–Њ –љ–∞—И —А—П–і –њ—А–Є –љ–µ–Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ —Г–≤–µ–ї–Є—З–µ–љ–Є–Є —З–Є—Б–ї–∞ —З–ї–µ–љ–Њ–≤ –њ—А–Є –љ–µ–Ї–Њ—В–Њ—А—Л—Е –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е —Г—Б–ї–Њ–≤–Є—П—Е, –љ–∞–Ї–ї–∞–і—Л–≤–∞–µ–Љ—Л—Е –љ–∞ —Д—Г–љ–Ї—Ж–Є—О
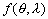 , —Б—Е–Њ–і–Є—В—Б—П. –Ю–і–љ–∞–Ї–Њ, –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ —Б–Ї–Њ—А–Њ—Б—В–Є —Н—В–Њ–є —Б—Е–Њ–і–Є–Љ–Њ—Б—В–Є –ї–µ–ґ–Є—В –Ј–∞ –њ—А–µ–і–µ–ї–∞–Љ–Є –љ–∞—И–µ–≥–Њ –Ї—Г—А—Б–∞.
, —Б—Е–Њ–і–Є—В—Б—П. –Ю–і–љ–∞–Ї–Њ, –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ —Б–Ї–Њ—А–Њ—Б—В–Є —Н—В–Њ–є —Б—Е–Њ–і–Є–Љ–Њ—Б—В–Є –ї–µ–ґ–Є—В –Ј–∞ –њ—А–µ–і–µ–ї–∞–Љ–Є –љ–∞—И–µ–≥–Њ –Ї—Г—А—Б–∞.
–Ш–љ—В–µ–≥—А–∞–ї—М–љ–∞—П —Д–Њ—А–Љ–∞ —А—П–і–∞ –Ы–∞–њ–ї–∞—Б–∞.
–Ь—Л —Г–ґ–µ –≥–Њ–≤–Њ—А–Є–ї–Є, —З—В–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –≤–Є–і–∞ (4.17) –µ—Б—В—М –∞–љ–∞–ї–Њ–≥ —А—П–і–∞ –§—Г—А—М–µ, –≤ –Ї–Њ—В–Њ—А–Њ–Љ —А–Њ–ї—М —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –≤—Л–њ–Њ–ї–љ—П—О—В —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є. –°—Г—Й–µ—Б—В–≤—Г–µ—В —В–∞–Ї–ґ–µ –Є –∞–љ–∞–ї–Њ–≥ –Є–љ—В–µ–≥—А–∞–ї–∞ –§—Г—А—М–µ вИЪ –Є–љ—В–µ–≥—А–∞–ї—М–љ–∞—П —Д–Њ—А–Љ–∞ —А—П–і–∞ –Ы–∞–њ–ї–∞—Б–∞. –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –µвХ¶ –њ–Њ–ї—Г—З–Є—В—М, –њ–Њ–і—Б—В–∞–≤–Є–Љ –≤ (4.17) –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ
 –Є
–Є  , –Ї–Њ—В–Њ—А—Л–µ –Њ–њ—А–µ–і–µ–ї—П—В—Б—П —Б –њ–Њ–Љ–Њ—Й—М—О –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ (4.16) .–Я–µ—А–µ–Љ–µ–љ–љ—Л–µ, –њ–Њ –Ї–Њ—В–Њ—А—Л–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—Б—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –Љ—Л –±—Г–і–µ–Љ –њ–Њ–Љ–µ—З–∞—В—М —И—В—А–Є—Е–Њ–Љ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
, –Ї–Њ—В–Њ—А—Л–µ –Њ–њ—А–µ–і–µ–ї—П—В—Б—П —Б –њ–Њ–Љ–Њ—Й—М—О –Є–љ—В–µ–≥—А–∞–ї–Њ–≤ (4.16) .–Я–µ—А–µ–Љ–µ–љ–љ—Л–µ, –њ–Њ –Ї–Њ—В–Њ—А—Л–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—Б—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –Љ—Л –±—Г–і–µ–Љ –њ–Њ–Љ–µ—З–∞—В—М —И—В—А–Є—Е–Њ–Љ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
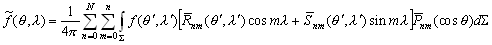 .
.
–Я—А–Є–љ–Є–Љ–∞—П –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ
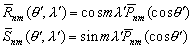 ,
,
–њ–Њ–ї—Г—З–Є–Љ
 . (4.18)
. (4.18)
–Ф–ї—П –і–∞–ї—М–љ–µ–є—И–µ–≥–Њ —Г–њ—А–Њ—Й–µ–љ–Є—П –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–є —Д–Њ—А–Љ—Г–ї—Л –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ–Њ–є —В–µ–Њ—А–µ–Љ–Њ–є —Б–ї–Њ–ґ–µ–љ–Є—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є.
–Я—Г—Б—В—М —В–Њ—З–Ї–∞ –† –Є–Љ–µ–µ—В –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л, –∞ —В–Њ—З–Ї–∞ Q –њ—А–Є–љ–∞–і–ї–µ–ґ–Є—В —Н–ї–µ–Љ–µ–љ—В—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є –Є–Љ–µ–µ—В —И—В—А–Є—Е–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —Ж–µ–љ—В—А–∞–ї—М–љ–Њ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г —Н—В–Є–Љ–Є –і–≤—Г–Љ—П —В–Њ—З–Ї–∞–Љ–Є –≥—А–µ—З–µ—Б–Ї–Њ–є –±—Г–Ї–≤–Њ–єY
. –Ґ–Њ–≥–і–∞ —В–µ–Њ—А–µ–Љ–∞ —Б–ї–Њ–ґ–µ–љ–Є—П –і–ї—П –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –≤—Л–≥–ї—П–і–Є—В —В–∞–Ї
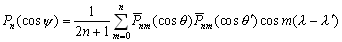 (4.19)
(4.19)
–Ґ–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Г (4.18) –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
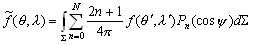 (4.20)
(4.20)
–Ъ–∞–ґ–і–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ –≤ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–µ —З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –Ы–∞–њ–ї–∞—Б–∞
 (4.21)
(4.21)
–Ы–µ–Ї—Ж–Є—П 5
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞. –†–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ —А—П–і –њ–Њ —И–∞—А–Њ–≤—Л–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ –°—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ. –У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В–µ–ї–∞ –≤—А–∞—Й–µ–љ–Є—П. –Я–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є.
–Я—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —А—П–і–Њ–Љ –Ы–∞–њ–ї–∞—Б–∞
–Э–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ –њ–Њ–і –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ –Ї–∞–Ї–Њ–є –ї–Є–±–Њ —Б–Є–ї—Л, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –Є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Љ—Л –±—Г–і–µ–Љ –њ–Њ–љ–Є–Љ–∞—В—М —Б–Є–ї–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О. –Ф–ї—П –љ–∞—З–∞–ї–∞ –Њ—Б—В–∞–љ–Њ–≤–Є–Љ—Б—П –љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–µ
—Б–Є–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П, –Ї–Њ—В–Њ—А—Л–є —З–∞—Й–µ –≤—Б–µ–≥–Њ –љ–∞–Ј—Л–≤–∞—О—В –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ. –Я—Г—Б—В—М —Н–ї–µ–Љ–µ–љ—В –Љ–∞—Б—Б—Л dm –љ–∞—Е–Њ–і–Є—В—Б—П –≤ —В–Њ—З–Ї–µ Q(x
,h
,V
), –∞ —В–Њ—З–Ї–∞ P(x,y,z) —Б —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –љ–∞—Е–Њ–і–Є—В—Б—П –≤–љ–µ –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ —В–µ–ї–∞. –†–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А, —Б–Њ–µ–і–Є–љ—П—О—Й–Є–є —В–Њ—З–Ї–Є –† –Є Q, –±—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М —З–µ—А–µ–Ј r, –∞ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А—Л —Н—В–Є—Е —В–Њ—З–µ–Ї —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —З–µ—А–µ–Ј 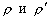 . –£–≥–Њ–ї –Љ–µ–ґ–і—Г —Н—В–Є–Љ–Є –≤–µ–Ї—В–Њ—А–∞–Љ–Є –±—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М —З–µ—А–µ–Ј f
. –Х—Б–ї–Є —В–Њ—З–Ї–∞ –Ю вИЪ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–Њ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ю–†Q —Б–ї–µ–і—Г–µ—В
. –£–≥–Њ–ї –Љ–µ–ґ–і—Г —Н—В–Є–Љ–Є –≤–µ–Ї—В–Њ—А–∞–Љ–Є –±—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М —З–µ—А–µ–Ј f
. –Х—Б–ї–Є —В–Њ—З–Ї–∞ –Ю вИЪ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–Њ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Ю–†Q —Б–ї–µ–і—Г–µ—В
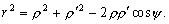
–Я–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —В–µ–ї–∞ –≤ —В–Њ—З–Ї–µ –† –Є–Љ–µ–µ—В –≤–Є–і
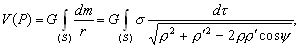 (5.1)
(5.1)
–≥–і–µ
 - —Н–ї–µ–Љ–µ–љ—В –Њ–±—КвХ¶–Љ–∞,
- —Н–ї–µ–Љ–µ–љ—В –Њ–±—КвХ¶–Љ–∞,  - –њ–ї–Њ—В–љ–Њ—Б—В—М. –Т—Л–љ–µ—Б–µ–Љ –Є–Ј-–њ–Њ–і –Ј–љ–∞–Ї–∞ –Ї–Њ—А–љ—П –≤–µ–ї–Є—З–Є–љ—Г r
>
r
¢
, –њ–Њ–ї—Г—З–Є–Љ
- –њ–ї–Њ—В–љ–Њ—Б—В—М. –Т—Л–љ–µ—Б–µ–Љ –Є–Ј-–њ–Њ–і –Ј–љ–∞–Ї–∞ –Ї–Њ—А–љ—П –≤–µ–ї–Є—З–Є–љ—Г r
>
r
¢
, –њ–Њ–ї—Г—З–Є–Љ
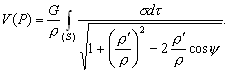
–Я–Њ–і –Ј–љ–∞–Ї–Њ–Љ –Є–љ—В–µ–≥—А–∞–ї–∞ —Б—В–Њ–Є—В –њ—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ (—Б–Љ. —Д–Њ—А–Љ—Г–ї—Г (4.1)
), –њ–Њ—Н—В–Њ–Љ—Г
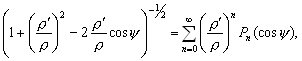
–≥–і–µ
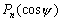 - –њ–Њ–ї–Є–љ–Њ–Љ –Ы–µ–ґ–∞–љ–і—А–∞ —Б—В–µ–њ–µ–љ–Є n.
- –њ–Њ–ї–Є–љ–Њ–Љ –Ы–µ–ґ–∞–љ–і—А–∞ —Б—В–µ–њ–µ–љ–Є n.
–Ґ–µ–њ–µ—А—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ –† –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
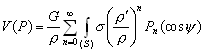 (5.2)
(5.2)
–Ъ–∞–ґ–і–Њ–µ –Њ—В–і–µ–ї—М–љ–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї—Л –µ—Б—В—М —Д—Г–љ–Ї—Ж–Є—П –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤–Њ –≤–љ–µ—И–љ–µ–є —В–Њ—З–Ї–µ. –Ю–±–Њ–Ј–љ–∞—З–Є–≤ –µвХ¶ —З–µ—А–µ–Ј
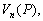 –њ–Њ–ї—Г—З–Є–Љ
–њ–Њ–ї—Г—З–Є–Љ
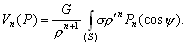 (5.3)
(5.3)
–Ґ–µ–њ–µ—А—М —А—П–і –Ы–∞–њ–ї–∞—Б–∞ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
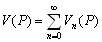 (5.4)
(5.4)
–§—Г–љ–Ї—Ж–Є–Є –Ы–∞–њ–ї–∞—Б–∞, –Ї–∞–Ї —Б–ї–µ–і—Г–µ—В –Є–Ј —Д–Њ—А–Љ—Г–ї—Л (5.3), –Ј–∞–≤–Є—Б—П—В –Њ—В —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –њ–ї–Њ—В–љ–Њ—Б—В–Є –≤–љ—Г—В—А–Є –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ —В–µ–ї–∞. –Я—А–Є–≤–µ–і–µ–љ–љ—Л–є –Є–љ—В–µ–≥—А–∞–ї –µ—Б—В—М –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, –Ї–Њ—В–Њ—А–∞—П, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б –њ–Њ–Љ–Њ—Й—М—О —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е –°—В–Њ–Ї—Б–∞, –Є–ї–Є, —Б—В–Њ–Ї—Б–Њ–≤—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е.
–Я–Њ—Б—В–Њ—П–љ–љ–Њ–є –°—В–Њ–Ї—Б–∞ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –≤–µ–ї–Є—З–Є–љ–∞, –Ї–Њ—В–Њ—А–∞—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
 , (5.5)
, (5.5)
–≥–і–µ
 –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –≤–љ—Г—В—А–Є –Њ–±—КвХ¶–Љ–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П.
–≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П –≤–љ—Г—В—А–Є –Њ–±—КвХ¶–Љ–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П.
–Т–µ—А–љвХ¶–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–µ (5.3). –Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є —Б–ї–Њ–ґ–µ–љ–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є (4.19). –ХвХ¶, –Њ—З–µ–≤–Є–і–љ–Њ, –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
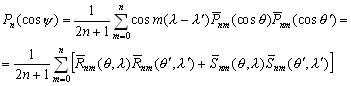
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
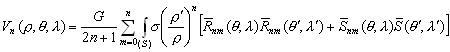 . (5.6)
. (5.6)
–§—Г–љ–Ї—Ж–Є–Є —В–µ–Ї—Г—Й–Є—Е (—И—В—А–Є—Е–Њ–≤–∞–љ–љ—Л—Е) –Ї–Њ–Њ—А–і–Є–љ–∞—В
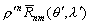 –Є
–Є 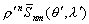 —П–≤–ї—П—О—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–Љ–Є, —В–∞–Ї –Ї–∞–Ї –Њ–љ–Є –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В –Ї —И–∞—А–Њ–≤—Л–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ –њ–µ—А–≤–Њ–≥–Њ —В–Є–њ–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О (5.5) –Є–љ—В–µ–≥—А–∞–ї—Л –≤–Є–і–∞
—П–≤–ї—П—О—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–Љ–Є, —В–∞–Ї –Ї–∞–Ї –Њ–љ–Є –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В –Ї —И–∞—А–Њ–≤—Л–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ –њ–µ—А–≤–Њ–≥–Њ —В–Є–њ–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О (5.5) –Є–љ—В–µ–≥—А–∞–ї—Л –≤–Є–і–∞ 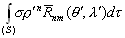 –Є
–Є 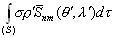 —П–≤–ї—П—О—В—Б—П —Б—В–Њ–Ї—Б–Њ–≤—Л–Љ–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є.
—П–≤–ї—П—О—В—Б—П —Б—В–Њ–Ї—Б–Њ–≤—Л–Љ–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є.
–Т–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П
 (5.7)
(5.7)
–Ч–і–µ—Б—М, –Ї–∞–Ї –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–Њ–Ј–ґ–µ —Г–±–µ–і–Є–Љ—Б—П, –Ь вИЪ –Љ–∞—Б—Б–∞ —В–µ–ї–∞, –∞ вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П, –Є–Љ–µ—О—Й–∞—П —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М –і–ї–Є–љ—Л, –∞
 –Є
–Є  –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Л–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –°—В–Њ–Ї—Б–∞.
–±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Л–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –°—В–Њ–Ї—Б–∞.
–Ґ–µ–њ–µ—А—М —Д—Г–љ–Ї—Ж–Є—О –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤–Њ –≤–љ–µ—И–љ–µ–є —В–Њ—З–Ї–µ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
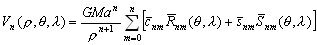 (5.8)
(5.8)
–°—Г–Љ–Љ–Є—А—Г—П –њ–Њ –≤—Б–µ–Љ
n , –њ–Њ–ї—Г—З–Є–Љ –Є—Б–Ї–Њ–Љ–Њ–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ —А—П–і –Ы–∞–њ–ї–∞—Б–∞
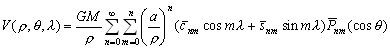 (5.9)
(5.9)
–Т—Б–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –Љ—Л –њ—А–Њ–≤–µ–ї–Є –і–ї—П –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є, –Њ—В–Љ–µ—З–∞—П –Є—Е —З–µ—А—В–Њ–є —Б–≤–µ—А—Е—Г. –Ю–і–љ–∞–Ї–Њ —Н—В–Є –ґ–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П —Б–њ—А–∞–≤–µ–і–ї–Є–≤—Л –Є –і–ї—П –љ–µ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –°—В–Њ–Ї—Б–∞ –±—Г–і—Г—В –Є–Љ–µ—В—М –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –Є–љ–Њ–є –≤–Є–і. –Ю–њ—Г—Б–Ї–∞—П –≤—Л–Ї–ї–∞–і–Ї–Є, –њ—А–Є–≤–µ–івХ¶–Љ –ї–Є—И—М –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г
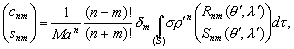 .(5.10)
.(5.10)
–≥–і–µ
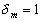 –њ—А–Є m=0 –Є
–њ—А–Є m=0 –Є 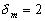 –њ—А–Є m¹
0 .
–њ—А–Є m¹
0 .
–Ь–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї —Б—В–Њ–Ї—Б–Њ–≤—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–љ–∞—З–∞–ї–∞ —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞
n =0.–Ґ–Њ–≥–і–∞ –Є —В=0, —В–∞–Ї –Ї–∞–Ї —Н—В–∞ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П –Є–Ј–Љ–µ–љ—П–µ—В—Б—П –Њ—В –љ—Г–ї—П –і–Њ –њ. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≥–∞—А–Љ–Њ–љ–Є–Ї–∞  —В–∞–Ї–ґ–µ —А–∞–≤–љ–∞ –љ—Г–ї—О, –Њ—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М —В–Њ–ї—М–Ї–Њ
—В–∞–Ї–ґ–µ —А–∞–≤–љ–∞ –љ—Г–ї—О, –Њ—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М —В–Њ–ї—М–Ї–Њ 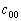 . –Ш–Ј —Д–Њ—А–Љ—Г–ї—Л (5.10) —Б–ї–µ–і—Г–µ—В
. –Ш–Ј —Д–Њ—А–Љ—Г–ї—Л (5.10) —Б–ї–µ–і—Г–µ—В
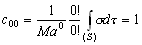
, –Є–±–Њ 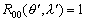 (5.11)
(5.11)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–µ–њ–µ—А—М —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞ –њ=1. –Ґ–µ–њ–µ—А—М –Љ—Л –і–Њ–ї–ґ–љ—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М —З–µ—В—Л—А–µ —Б—В–Њ–Ї—Б–Њ–≤—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е:
 –Ю–±—А–∞—Й–∞—П—Б—М –Ї —Д–Њ—А–Љ—Г–ї–µ (5.10), –њ–Њ–ї—Г—З–Є–Љ.
–Ю–±—А–∞—Й–∞—П—Б—М –Ї —Д–Њ—А–Љ—Г–ї–µ (5.10), –њ–Њ–ї—Г—З–Є–Љ.
 (5.12)
(5.12)
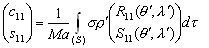 (5.13)
(5.13)
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –≤—Л–њ–Њ–ї–љ–Є—В—М –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ, –љ—Г–ґ–љ–Њ –њ–µ—А–µ–є—В–Є –Ї –і–µ–Ї–∞—А—В–Њ–≤—Л–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ
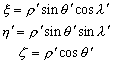 (5.14)
(5.14)
–Я–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ
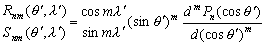 (5.15)
(5.15)
–Я—А–Є –њ=1 –Є–Љ–µ–µ–Љ
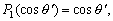 –њ–Њ—Н—В–Њ–Љ—Г
–њ–Њ—Н—В–Њ–Љ—Г
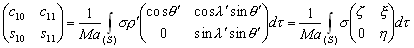
–Ш–Ј —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —Ж–µ–љ—В—А–∞ –Љ–∞—Б—Б —В–µ–ї–∞ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ

–њ–Њ—Н—В–Њ–Љ—Г
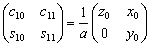 (5.16)
(5.16)
–Ш—В–∞–Ї, —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–µ—А–≤–Њ–є —Б—В–µ–њ–µ–љ–Є, –Ї–Њ—В–Њ—А—Г—О –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —Д—Г–љ–Ї—Ж–Є—П –Ы–∞–њ–ї–∞—Б–∞ –њ–µ—А–≤–Њ–є —Б—В–µ–њ–µ–љ–Є, –Њ–њ—А–µ–і–µ–ї—П–µ—В —Ж–µ–љ—В—А –Љ–∞—Б—Б –њ—А–Є—В—П–≥–Є–≤–∞—О—Й–µ–≥–Њ —В–µ–ї–∞. –Ю–њ—А–µ–і–µ–ї–Є–Љ —В–µ–њ–µ—А—М —Д—Г–љ–Ї—Ж–Є—О –Ы–∞–њ–ї–∞—Б–∞ –≤—В–Њ—А–Њ–є —Б—В–µ–њ–µ–љ–Є. –Ш–Ј —Д–Њ—А–Љ—Г–ї—Л (5.7) —Б–ї–µ–і—Г–µ—В
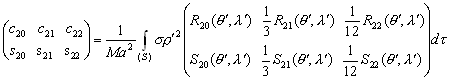
–°–љ–Њ–≤–∞ –њ–µ—А–µ–є–івХ¶–Љ –Ї –і–µ–Ї–∞—А—В–Њ–≤—Л–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ
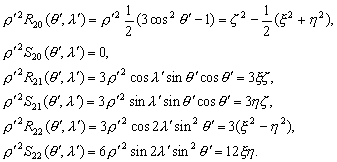 (5.17)
(5.17)
–°–ї–µ–і—Г—П –њ—А–∞–≤–Є–ї–∞–Љ —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є, –≤—Л–њ–Њ–ї–љ–Є–Љ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ. –С—Г–і–µ–Љ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —В—А–∞–і–Є—Ж–Є–Њ–љ–љ—Л–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –і–ї—П –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Љ–∞—Б—Б—Л –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ - –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Є–љ–µ—А—Ж–Є–Є
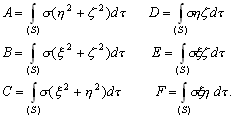 (5.18)
(5.18)
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Є–≤–µ—Б—В–Є —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Ї –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ–Љ—Г –≤–Є–і—Г, –Ј–∞–Љ–µ—В–Є–Љ, —З—В–Њ
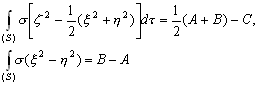
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Љ–∞—В—А–Є—Ж—Г, —Б–Њ—Б—В–∞–≤–ї–µ–љ–љ—Г—О –Є–Ј –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –і–ї—П —И–∞—А–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤—В–Њ—А–Њ–є —Б—В–µ–њ–µ–љ–Є, –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ
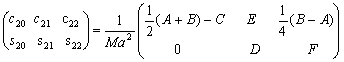 (5.19)
(5.19)
–Т–µ—А–љвХ¶–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —А—П–і–Њ–Љ –Ы–∞–њ–ї–∞—Б–∞. –Ю–њ—А–µ–і–µ–ї—П—П —Б—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ —З–µ—А–µ–Ј –љ–µ–љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–µ —И–∞—А–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є, —Д–Њ—А–Љ—Г–ї–∞ (5.9) –±—Г–і–µ—В –Є–Љ–µ—В—М —В–Њ—В –ґ–µ –≤–Є–і, –Ј–∞ –Є—Б–Ї–ї—О—З–µ–љ–Є–µ–Љ —В–Њ–≥–Њ, —З—В–Њ —Б—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є вМ†–њ–Њ—В–µ—А—П—О—ВвЦ† —З–µ—А—В—Г —Б–≤–µ—А—Е—Г
вИЪ —Д–Њ—А–Љ—Г–ї–∞ (5.20):
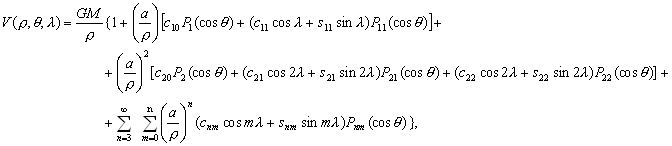
–≥–і–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —Б
nm –Є snm –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Д–Њ—А–Љ—Г–ї–∞–Љ–Є (5.10), (5.16) –Є (5.19). –Я–Њ–ї—Г—З–µ–љ–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г –Љ–Њ–ґ–љ–Њ —Г–њ—А–Њ—Б—В–Є—В—М, –µ—Б–ї–Є –њ—А–Є–љ—П—В—М
1)
–љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б, 2) –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –Њ—Б–µ–є —Б–Њ–≤–њ–∞–і–∞—О—В —Б –≥–ї–∞–≤–љ—Л–Љ–Є –Њ—Б—П–Љ–Є –Є–љ–µ—А—Ж–Є–Є.
–Я—А–Є –≤—Л–њ–Њ–ї–љ–µ–љ–Є–Є —Н—В–Є—Е —Г—Б–ї–Њ–≤–Є–є —Д—Г–љ–Ї—Ж–Є—П –Ы–∞–њ–ї–∞—Б–∞ –њ–µ—А–≤–Њ–є —Б—В–µ–њ–µ–љ–Є –±—Г–і–µ—В —А–∞–≤–љ–∞ –љ—Г–ї—О, —В–Њ –µ—Б—В—М
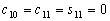 . –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –±—Г–і—Г—В —А–∞–≤–љ—Л –љ—Г–ї—О –Є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Є–љ–µ—А—Ж–Є–Є D, E, F. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –±—Г–і—Г—В —А–∞–≤–љ—Л –љ—Г–ї—О –Є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Є–љ–µ—А—Ж–Є–Є D, E, F. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, 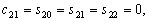 –∞
–∞
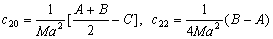 .
.
–Ґ–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї–∞ (5.20) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
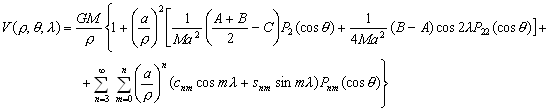 (5.21)
(5.21)
–Я–Њ–ї—Г—З–µ–љ–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ –≥–Њ–≤–Њ—А–Є—В –Њ —В–Њ–Љ, —З—В–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ —В–Њ—З–Ї–µ –† –Ј–∞–≤–Є—Б–Є—В –Ї–∞–Ї –Њ—В —А–∞—Б—Б—В–Њ—П–љ–Є—П —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–є —В–Њ—З–Ї–Є –Њ—В –љ–∞—З–∞–ї–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–∞–Ї –Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В: –њ–Њ–ї—П—А–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Є –і–Њ–ї–≥–Њ—В—Л. –Ю–і–љ–∞–Ї–Њ –Њ—В–і–µ–ї—М–љ—Л–µ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –Љ–Њ–≥—Г—В –Ј–∞–≤–Є—Б–µ—В—М —В–Њ–ї—М–Ї–Њ –Њ—В —И–Є—А–Њ—В—Л, –љ–∞–њ—А–Є–Љ–µ—А, –њ—А–Є —В=0, –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –љ–∞–Ј—Л–≤–∞—О—В –Ј–Њ–љ–∞–ї—М–љ—Л–Љ–Є. –Я–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Б—Д–µ—А—Л –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П —А–∞–Ј–±–Є—В–Њ–є –љ–∞ –Ј–Њ–љ—Л вИЪ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ –њ–Њ—П—Б–∞ .
–Т—В–Њ—А–Њ–є –Ї—А–∞–є–љ–Є–є —Б–ї—Г—З–∞–є –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –њ—А–Є —В=–њ. –Ю–±—А–∞—В–Є–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–µ (5.15). –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –Њ–љ–∞ –њ—А–Є–Њ–±—А–µ—В–∞–µ—В –≤–Є–і
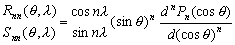
–Э–µ—В—А—Г–і–љ–Њ –њ–Њ–љ—П—В—М, —З—В–Њ –Ј–љ–∞–Ї —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П –≥–∞—А–Љ–Њ–љ–Є–Ї–∞ –Љ–Њ–ґ–µ—В –Љ–µ–љ—П—В—М –њ—А–Є –Њ–њ—А–µ–і–µ–ївХ¶–љ–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –і–Њ–ї–≥–Њ—В—Л, —В–∞–Ї –Ї–∞–Ї –њ-–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ–ї–Є–љ–Њ–Љ–∞ –њ-–Њ–є —Б—В–µ–њ–µ–љ–Є –µ—Б—В—М –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, –∞
 –њ—А–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–Є –њ–Њ–ї—П—А–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В –љ—Г–ї—П –і–Њ p
–љ–µ –Љ–µ–љ—П–µ—В –Ј–љ–∞–Ї–∞. –Я–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Б—Д–µ—А—Л –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П —А–∞–Ј–±–Є—В–Њ–є –њ–Њ–і–Њ–±–љ–Њ –∞—А–±—Г–Ј—Г –љ–∞ —Б–µ–Ї—В–Њ—А–∞ –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є, –љ–∞–Ј—Л–≤–∞—О—В—Б—П —Б–µ–Ї—В–Њ—А–Є–∞–ї—М–љ—Л–Љ–Є.
–њ—А–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–Є –њ–Њ–ї—П—А–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В –љ—Г–ї—П –і–Њ p
–љ–µ –Љ–µ–љ—П–µ—В –Ј–љ–∞–Ї–∞. –Я–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Б—Д–µ—А—Л –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П —А–∞–Ј–±–Є—В–Њ–є –њ–Њ–і–Њ–±–љ–Њ –∞—А–±—Г–Ј—Г –љ–∞ —Б–µ–Ї—В–Њ—А–∞ –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є, –љ–∞–Ј—Л–≤–∞—О—В—Б—П —Б–µ–Ї—В–Њ—А–Є–∞–ї—М–љ—Л–Љ–Є.
–Э–∞–Ї–Њ–љ–µ—Ж, –≤ –Њ—Б—В–∞–ї—М–љ—Л—Е —Б–ї—Г—З–∞—П—Е –≥—А–∞–љ–Є—Ж—Л –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Ј–љ–∞–Ї–∞ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л –Њ–±—А–∞–Ј—Г—О—В –Љ–Њ–Ј–∞–Є–Ї—Г –њ–Њ–і–Њ–±–љ–Њ —И–∞—Е–Љ–∞—В–љ–Њ–є –і–Њ—Б–Ї–µ. –≠—В–Є –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –љ–∞–Ј—Л–≤–∞—О—В —В–µ—Б—Б–µ—А–∞–ї—М–љ—Л–Љ–Є –Њ—В –ї–∞—В–Є–љ—Б–Ї–Њ–≥–Њ —Б–ї–Њ–≤–∞
tessera, —З—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–є —З–µ—В—Л—АвХ¶—Е—Г–≥–Њ–ї—М–љ–Є–Ї –≤ –Љ–Њ–Ј–∞–Є–Ї–µ.
–Ф–ї—П –Љ–љ–Њ–≥–Є—Е –Ј–∞–і–∞—З –љ–µ–±–µ—Б–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є —Б–Є–ї–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О –њ–ї–∞–љ–µ—В—Л –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А—Г—О—В —В–Њ–ї—М–Ї–Њ –Ј–Њ–љ–∞–ї—М–љ—Л–Љ–Є –≥–∞—А–Љ–Њ–љ–Є–Ї–∞–Љ–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –Љ—Л –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ–Љ, —З—В–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–∞—П –њ–ї–∞–љ–µ—В–∞ –µ—Б—В—М —В–µ–ї–Њ –≤—А–∞—Й–µ–љ–Є—П –Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —Б–Є–ї—Л –њ—А–Є—В—П–ґ–µ–љ–Є—П –Њ—В –і–Њ–ї–≥–Њ—В—Л —В–Њ—З–Ї–Є, –і–ї—П –Ї–Њ—В–Њ—А–Њ–є –±–µ—АвХ¶—В—Б—П —Б–Є–ї–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В. –Ґ–Њ–≥–і–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –Ј–∞–њ–Є—Б—Л–≤–∞—О—В –≤ –≤–Є–і–µ
 , (5.22)
, (5.22)
–≥–і–µ
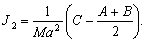 –≠—В—Г –њ–Њ—Б—В–Њ—П–љ–љ—Г—О –Њ—В–љ–Њ—Б—П—В –Ї —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ. –Х—Б–ї–Є –њ–ї–∞–љ–µ—В–∞ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —В–µ–ї–Њ –≤—А–∞—Й–µ–љ–Є—П, —В–Њ –Р=–Т –Є
–≠—В—Г –њ–Њ—Б—В–Њ—П–љ–љ—Г—О –Њ—В–љ–Њ—Б—П—В –Ї —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ. –Х—Б–ї–Є –њ–ї–∞–љ–µ—В–∞ –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —В–µ–ї–Њ –≤—А–∞—Й–µ–љ–Є—П, —В–Њ –Р=–Т –Є 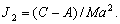 –Ю–љ–∞ –Ј–∞–≤–Є—Б–Є—В –ї–Є—И—М –Њ—В –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Є–љ–µ—А—Ж–Є–Є, —В–Њ –µ—Б—В—М –Њ—В –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Љ–∞—Б—Б –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Ю—Б—В–∞–ї—М–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –љ–∞–Ј—Л–≤–∞—О—В –Љ—Г–ї—М—В–Є–њ–Њ–ї—М–љ—Л–Љ–Є –Љ–Њ–Љ–µ–љ—В–∞–Љ–Є –Љ–∞—Б—Б—Л. –Ю–љ–Є –љ–µ –Є–Љ–µ—О—В —Б—В–Њ–ї—М —П—Б–љ–Њ–≥–Њ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞.
–Ю–љ–∞ –Ј–∞–≤–Є—Б–Є—В –ї–Є—И—М –Њ—В –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Є–љ–µ—А—Ж–Є–Є, —В–Њ –µ—Б—В—М –Њ—В –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Љ–∞—Б—Б –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Ю—Б—В–∞–ї—М–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –љ–∞–Ј—Л–≤–∞—О—В –Љ—Г–ї—М—В–Є–њ–Њ–ї—М–љ—Л–Љ–Є –Љ–Њ–Љ–µ–љ—В–∞–Љ–Є –Љ–∞—Б—Б—Л. –Ю–љ–Є –љ–µ –Є–Љ–µ—О—В —Б—В–Њ–ї—М —П—Б–љ–Њ–≥–Њ –Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Љ—Л—Б–ї–∞.
–Я–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є
–°–Є–ї–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О —Г–і–µ–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Њ–±—Л—З–љ–Њ –љ–∞–Ј—Л–≤–∞—О—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Я–Њ–і —Б–Є–ї–Њ–є —В—П–ґ–µ—Б—В–Є —З–∞—Б—В–Њ –њ–Њ–љ–Є–Љ–∞—О—В —Б–Є–ї—Г, —Б –Ї–Њ—В–Њ—А–Њ–є –≤—Б—П–Ї–Њ–µ —В–µ–ї–Њ –њ—А–Є—В—П–≥–Є–≤–∞–µ—В—Б—П –Ї –Ч–µ–Љ–ї–µ (—Б–Љ., –љ–∞–њ—А–Є–Љ–µ—А, –Ы.–Т.–°–Њ—А–Њ–Ї–Є–љ –У—А–∞–≤–Є–Љ–µ—В—А–Є—П –Є –≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П —А–∞–Ј–≤–µ–і–Ї–∞.
–У–Њ—Б—В–Њ–њ—В–µ—Е–Є–Ј–і–∞—В –Ь.1953). –Ь–Њ–ї—З–∞–ї–Є–≤–Њ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ —Н—В–Њ —В–µ–ї–Њ –Є–Љ–µ–µ—В –Љ–∞—Б—Б—Г, —А–∞–≤–љ—Г—О –µ–і–Є–љ–Є—Ж–µ. –Я–Њ—Н—В–Њ–Љ—Г —А–µ—З—М –Є–івХ¶—В –Њ–± —Г–і–µ–ї—М–љ–Њ–є —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –љ–∞–±–ї—О–і–µ–љ–Є—П –Ј–∞ –і–µ–є—Б—В–≤–Є–µ–Љ —Б–Є–ї—Л –њ—А–Њ–≤–Њ–і—П—В—Б—П –≤–Њ –≤—А–∞—Й–∞—О—Й–µ–є—Б—П –≤–Љ–µ—Б—В–µ —Б –Ч–µ–Љ–ї–µ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–Њ –µ—Б—В—М –≤ –љ–µ–Є–љ–µ—А—Ж–Є–∞–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ –Њ—В—Б—ЗвХ¶—В–∞. –Э–∞ –њ—А–Њ–±–љ–Њ–µ —В–µ–ї–Њ, –µ—Б–ї–Є –љ–µ—В —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л—Е –Њ–≥–Њ–≤–Њ—А–Њ–Ї, –і–µ–є—Б—В–≤—Г—О—В –ї–Є—И—М –і–≤–µ —Д–Є–Ј–Є—З–µ—Б–Ї–Є–µ —Б–Є–ї—Л: —Б–Є–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П —Б–Њ —Б—В–Њ—А–Њ–љ—Л –Ч–µ–Љ–ї–Є –Є —Г–њ—А—Г–≥–∞—П —Б–Є–ї–∞ —А–µ–∞–Ї—Ж–Є–Є –Њ–њ–Њ—А—Л. –†–µ–Ј—Г–ї—М—В–Є—А—Г—О—Й–∞—П —Н—В–Є—Е –і–≤—Г—Е —Б–Є–ї –љ–µ —А–∞–≤–љ–∞ –љ—Г–ї—О. –°—Г–Љ–Љ—Л –Є—Е –і–∞вХ¶—В –Ї–∞–Ї —А–∞–Ј —В—Г —Б–Є–ї—Г, –Ї–Њ—В–Њ—А–∞—П —Б–Њ–Њ–±—Й–∞–µ—В –њ—А–Њ–±–љ–Њ–Љ—Г —В–µ–ї—Г —Г—Б–Ї–Њ—А–µ–љ–Є–µ, —Б –Ї–Њ—В–Њ—А—Л–Љ —В–µ–ї–Њ —Б–Њ–≤–µ—А—И–∞–µ—В –і–≤–Є–ґ–µ–љ–Є–µ –њ–Њ –Ї—А—Г–≥–Њ–≤–Њ–є —В—А–∞–µ–Ї—В–Њ—А–Є–Є –≤ –њ—А–Њ—Ж–µ—Б—Б–µ —Б—Г—В–Њ—З–љ–Њ–≥–Њ –≤—А–∞—Й–µ–љ–Є—П. –°–Њ–≥–ї–∞—Б–љ–Њ —В—А–µ—В—М–µ–Љ—Г –Ј–∞–Ї–Њ–љ—Г –Љ–µ—Е–∞–љ–Є–Ї–Є –њ—А–Њ–±–љ–Њ–µ —В–µ–ї–Њ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤—Г–µ—В —Б –Њ–њ–Њ—А–Њ–є, –Њ–љ–Њ –і–∞–≤–Є—В –љ–∞ –Њ–њ–Њ—А—Г —Б —В–Њ–є –ґ–µ —Б–∞–Љ–Њ–є —Б–Є–ї–Њ–є, —З—В–Њ –Є –Њ–њ–Њ—А–∞ –і–∞–≤–Є—В –љ–∞ —В–µ–ї–Њ. –Ґ—П–ґ–µ—Б—В—М –њ—А–Њ–±–љ–Њ–≥–Њ —В–µ–ї–∞ —Б–Њ–Ј–і–∞вХ¶—В —А–µ–∞–Ї—Ж–Є—П –Њ–њ–Њ—А—Л (–њ–Њ–і—Б—В–∞–≤–Ї–Є). –≠—В—Г —Б–Є–ї—Г –љ–∞–Ј—Л–≤–∞—О—В –≤–µ—Б–Њ–Љ —В–µ–ї–∞. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ –≤–µ—Б —В–µ–ї–∞ –µ—Б—В—М —Б–Є–ї–∞, —А–∞–≤–љ–∞—П —А–∞–≤–љ–Њ–і–µ–є—Б—В–≤—Г—О—Й–µ–є —Б–Є–ї—Л –њ—А–Є—В—П–ґ–µ–љ–Є—П –Є —Б–Є–ї—Л –Є–љ–µ—А—Ж–Є–Є, –Ї–Њ—В–Њ—А—Г—О –њ—А–Є–љ—П—В–Њ –љ–∞–Ј—Л–≤–∞—В—М —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї–Њ–є. –Ш—В–∞–Ї, —Г–і–µ–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –µ—Б—В—М –≤–µ—Б —В–µ–ї–∞ –µ–і–Є–љ–Є—З–љ–Њ–є –Љ–∞—Б—Б—Л, –љ–µ–њ–Њ–і–≤–Є–ґ–љ–Њ–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є (–Є–ї–Є –Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –і—А—Г–≥–Њ–є –њ–ї–∞–љ–µ—В—Л). –£–і–µ–ї—М–љ–∞—П —Б–Є–ї–∞ –Є–Љ–µ–µ—В —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—М —Г—Б–Ї–Њ—А–µ–љ–Є—П, –њ–Њ—Н—В–Њ–Љ—Г —З–∞—Б—В–Њ –≤–Љ–µ—Б—В–Њ —В–µ—А–Љ–Є–љ–∞ —Г–і–µ–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –≥–Њ–≤–Њ—А—П—В —Г—Б–Ї–Њ—А–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Э–∞ –∞–љ–≥–ї–Є–є—Б–Ї–Њ–Љ —П–Ј—Л–Ї–µ —Г—Б–Ї–Њ—А–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞–Ј—Л–≤–∞—О—В gravity, –љ–∞ –љ–µ–Љ–µ—Ж–Ї–Њ–Љ вИЪ schwehre, –≤ –Њ–±–Њ–Є—Е —Б–ї—Г—З–∞—П—Е —Н—В–Є —Б–ї–Њ–≤–∞ –Њ–±–Њ–Ј–љ–∞—З–∞—О—В —В—П–ґ–µ—Б—В—М.
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –Ј–∞–њ–Є—Б–∞—В—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Б–Є–ї—Л –њ—А–Є—В—П–ґ–µ–љ–Є—П —Б–ї–Њ–ґ–Є—В—М —Б —Б–Є–ї–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є –і–ї—П —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л. –≠—В—Г —Б–Є–ї–Њ–≤—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤ –і–∞–ї—М–љ–µ–є—И–µ–Љ –±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ —В—П–ґ–µ—Б—В–Є:
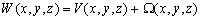 ,
,
–≥–і–µ
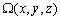 - —Б–Є–ї–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –і–ї—П —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –Є–љ–µ—А—Ж–Є–Є, –Ї–Њ—В–Њ—А—Г—О –Љ—Л —Г—Б–ї–Њ–≤–љ–Њ –±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ. –Х—Б–ї–Є –Њ—Б—М –Юz –≤—Л–±—А–∞—В—М —В–∞–Ї, —З—В–Њ–±—Л –Њ–љ–∞ —Б—В—А–Њ–≥–Њ —Б–Њ–≤–њ–∞–і–∞–ї–∞ —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є, —В–Њ —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
- —Б–Є–ї–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –і–ї—П —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –Є–љ–µ—А—Ж–Є–Є, –Ї–Њ—В–Њ—А—Г—О –Љ—Л —Г—Б–ї–Њ–≤–љ–Њ –±—Г–і–µ–Љ –љ–∞–Ј—Л–≤–∞—В—М —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–Љ. –Х—Б–ї–Є –Њ—Б—М –Юz –≤—Л–±—А–∞—В—М —В–∞–Ї, —З—В–Њ–±—Л –Њ–љ–∞ —Б—В—А–Њ–≥–Њ —Б–Њ–≤–њ–∞–і–∞–ї–∞ —Б –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є, —В–Њ —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
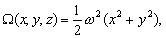
–Є–ї–Є –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е
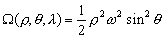 . (5.23)
. (5.23)
–Я–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П, —В–Њ –µ—Б—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —А–∞–≤–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ (—Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О) –љ–∞–Ј—Л–≤–∞—О—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –Є–Љ–µ—О—Й–µ–є —Г—А–∞–≤–љ–µ–љ–Є–µ
 .
.
–Т –Њ—В–ї–Є—З–Є–µ –Њ—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –љ–µ —П–≤–ї—П–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є, –Є–±–Њ
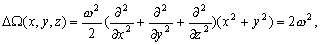
–њ–Њ—Н—В–Њ–Љ—Г
–≤–љ–µ —В–µ–ї–∞, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О S, –±—Г–і–µ—В –Є–Љ–µ—В—М –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ
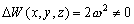 (5.24)
(5.24)
–Я—А–µ–і–µ–ї—Л –Я—Г–∞–љ–Ї–∞—А–µ –Є –Ъ—А—Г–і–µ–ї–Є –і–ї—П —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П —Д–Є–≥—Г—А—Л —А–∞–≤–љ–Њ–≤–µ—Б–Є—П
–Я–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Д–Є–≥—Г—А—Л —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є
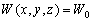 . –Ю–љ–∞ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П. –Я–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –љ–∞ —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є - –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю–і–љ–∞–Ї–Њ, –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Н—В–Њ —В–µ–ї–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –±—Л–ї–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–љ—Г—В—А—М —Н—В–Њ–≥–Њ —В–µ–ї–∞. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ (—Б–Є–ї–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є) –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞:
. –Ю–љ–∞ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П. –Я–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –љ–∞ —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є - –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю–і–љ–∞–Ї–Њ, –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Н—В–Њ —В–µ–ї–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –±—Л–ї–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–љ—Г—В—А—М —Н—В–Њ–≥–Њ —В–µ–ї–∞. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ (—Б–Є–ї–Њ–≤–Њ–є —Д—Г–љ–Ї—Ж–Є–Є) –і–Њ–ї–ґ–љ–∞ –±—Л—В—М –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞: 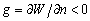 . –Я—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ
. –Я—А–Є–Љ–µ–љ–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –Ю—Б—В—А–Њ–≥—А–∞–і—Б–Ї–Њ–≥–Њ
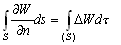 (5.25)
(5.25)
–Т–љ—Г—В—А–Є —В–µ–ї–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –љ–µ —П–≤–ї—П–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є, –Є–±–Њ D
V=-
4p
Gs
. –Я–Њ—Н—В–Њ–Љ—Г D
W=-
4p
Gs
+2w
2. –Я–µ—А–µ–њ–Є—И–µ–Љ —Д–Њ—А–Љ—Г–ї—Г (5.25) –≤ –≤–Є–і–µ
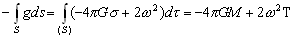 ,
,
–≥–і–µ –Ь вИЪ –Љ–∞—Б—Б–∞ –њ–ї–∞–љ–µ—В—Л, –∞ –Ґ вИЪ –µвХ¶ –Њ–±—КвХ¶–Љ. –£—Б–ї–Њ–≤–Є–µ —Б–Њ—Е—А–∞–љ–µ–љ–Є–µ –њ–ї–∞–љ–µ—В, –Ї–∞–Ї —В–≤–µ—А–і–Њ–≥–Њ —В–µ–ї–∞ вИЪ –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –њ–Њ—Н—В–Њ–Љ—Г –ї–µ–≤–∞—П —З–∞—Б—В—М –њ–Њ–ї—Г—З–µ–љ–љ–Њ–≥–Њ —А–∞–≤–µ–љ—Б—В–≤–∞ –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
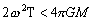 . –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —Г–≥–ї–Њ–≤–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л –љ–µ –Љ–Њ–ґ–µ—В –њ—А–µ–≤–Њ—Б—Е–Њ–і–Є—В—М –≤–µ–ї–Є—З–Є–љ—Л
. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —Г–≥–ї–Њ–≤–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л –љ–µ –Љ–Њ–ґ–µ—В –њ—А–µ–≤–Њ—Б—Е–Њ–і–Є—В—М –≤–µ–ї–Є—З–Є–љ—Л 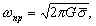 –≥–і–µ
–≥–і–µ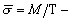 —Б—А–µ–і–љ—П—П –њ–ї–Њ—В–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л. –≠—В–Њ –µ—Б—В—М –њ—А–µ–і–µ–ї –Я—Г–∞–љ–Ї–∞—А–µ –і–ї—П —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П –њ–ї–∞–љ–µ—В—Л.
—Б—А–µ–і–љ—П—П –њ–ї–Њ—В–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л. –≠—В–Њ –µ—Б—В—М –њ—А–µ–і–µ–ї –Я—Г–∞–љ–Ї–∞—А–µ –і–ї—П —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П –њ–ї–∞–љ–µ—В—Л.
–Ф–ї—П –Ч–µ–Љ–ї–Є
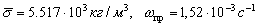 , —В–Њ –µ—Б—В—М –њ—А–µ–і–µ–ї—М–љ—Л–є –њ–µ—А–Є–Њ–і –≤—А–∞—Й–µ–љ–Є—П –і–ї—П –Ч–µ–Љ–ї–Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В 4125 —Б=1,14 —З–∞—Б.
, —В–Њ –µ—Б—В—М –њ—А–µ–і–µ–ї—М–љ—Л–є –њ–µ—А–Є–Њ–і –≤—А–∞—Й–µ–љ–Є—П –і–ї—П –Ч–µ–Љ–ї–Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В 4125 —Б=1,14 —З–∞—Б.
–Я—А–µ–і–µ–ї –Я—Г–∞–љ–Ї–∞—А–µ –љ–µ –≥–∞—А–∞–љ—В–Є—А—Г–µ—В —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В—М –њ–Њ–Ї–Њ—П –≤—Б–µ—Е —В–µ–ї, –ї–µ–ґ–∞—Й–Є—Е –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ь–Њ–ґ–µ—В —В–∞–Ї —Б–ї—Г—З–Є—В—М—Б—П, —З—В–Њ
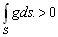 , –љ–Њ –љ–∞ –Њ—В–і–µ–ї—М–љ—Л—Е —Г—З–∞—Б—В–Ї–∞—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞, —В–Њ –µ—Б—В—М –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–≤–µ—А—Е! –£—Б—В–Њ–є—З–Є–≤–Њ—Б—В—М –њ–Њ–Ї–Њ—П —В–µ–ї –±—Г–і–µ—В –Њ–±–µ—Б–њ–µ—З–µ–љ–∞, –µ—Б–ї–Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П, —Б–Њ–≤–њ–∞–і–∞—О—Й–∞—П —Б –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л, –±—Г–і–µ—В –≤—Б–µ–≥–і–∞ –≤—Л–њ—Г–Ї–ї–Њ–є. –Ф–ї—П —Н—В–Њ–≥–Њ —Г—Б–ї–Њ–≤–Є—П –Є—В–∞–ї—М—П–љ—Б–Ї–Є–є —Г—ЗвХ¶–љ—Л–є –Ъ—А—Г–і–µ–ї–Є –і–ї—П –Њ–і–љ–Њ—А–Њ–і–љ–Њ–є –њ–ї–∞–љ–µ—В—Л —Б–љ–Є–Ј–Є–ї –њ—А–µ–і–µ–ї –і–ї—П —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П –≤
, –љ–Њ –љ–∞ –Њ—В–і–µ–ї—М–љ—Л—Е —Г—З–∞—Б—В–Ї–∞—Е –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ–∞, —В–Њ –µ—Б—В—М –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–≤–µ—А—Е! –£—Б—В–Њ–є—З–Є–≤–Њ—Б—В—М –њ–Њ–Ї–Њ—П —В–µ–ї –±—Г–і–µ—В –Њ–±–µ—Б–њ–µ—З–µ–љ–∞, –µ—Б–ї–Є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П, —Б–Њ–≤–њ–∞–і–∞—О—Й–∞—П —Б –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л, –±—Г–і–µ—В –≤—Б–µ–≥–і–∞ –≤—Л–њ—Г–Ї–ї–Њ–є. –Ф–ї—П —Н—В–Њ–≥–Њ —Г—Б–ї–Њ–≤–Є—П –Є—В–∞–ї—М—П–љ—Б–Ї–Є–є —Г—ЗвХ¶–љ—Л–є –Ъ—А—Г–і–µ–ї–Є –і–ї—П –Њ–і–љ–Њ—А–Њ–і–љ–Њ–є –њ–ї–∞–љ–µ—В—Л —Б–љ–Є–Ј–Є–ї –њ—А–µ–і–µ–ї –і–ї—П —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П –≤ 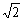 —А–∞–Ј:
—А–∞–Ј: 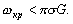 –Я–µ—А–Є–Њ–і –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—А–µ–і–µ–ї—Г –Ъ—А—Г–і–µ–ї–Є –љ–µ –і–Њ–ї–ґ–µ–љ –±—Л—В—М –Љ–µ–љ—М—И–µ 1,61 —З–∞—Б–∞.
–Я–µ—А–Є–Њ–і –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—А–µ–і–µ–ї—Г –Ъ—А—Г–і–µ–ї–Є –љ–µ –і–Њ–ї–ґ–µ–љ –±—Л—В—М –Љ–µ–љ—М—И–µ 1,61 —З–∞—Б–∞.
–Ы–µ–Ї—Ж–Є—П 6
–Э–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є. –І–µ—В—Л—А–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є. –°—Д–µ—А–Њ–Є–і –Ъ–ї–µ—А–Њ. –Ґ–µ–Њ—А–µ–Љ–∞ –°—В–Њ–Ї—Б–∞. –У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –£—Б–ї–Њ–≤–Є—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П.
–Э–Њ—А–Љ–∞–ї—М–љ–∞—П –Ч–µ–Љ–ї—П
–Ґ–µ—А–Љ–Є–љ –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –Ч–µ–Љ–ї—П - —В—А–∞–і–Є—Ж–Є–Њ–љ–љ—Л–є —Б—А–µ–і–Є —Б–њ–µ—Ж–Є–∞–ї–Є—Б—В–Њ–≤-–≥–µ–Њ–і–µ–Ј–Є—Б—В–Њ–≤. –°–ї–Њ–≤–Њ –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є, –≤—Л—Б–Њ—В–µ –Є —В.–њ.
, –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–Љ–µ—В—А —П–≤–ї—П–µ—В—Б—П –њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ—Л–Љ. –Х–≥–Њ –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ –Є–Ј–≤–µ—Б—В–љ—Л–Љ —Д–Њ—А–Љ—Г–ї–∞–Љ. –Э–Њ—А–Љ–∞–ї—М–љ–∞—П –Ч–µ–Љ–ї—П - —Н—В–Њ —В–µ–ї–Њ –Њ—В—Б—З–µ—В–∞ –і–ї—П –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –Ї–∞—А—В –≤—Л—Б–Њ—В, –≥–ї—Г–±–Є–љ –Љ–Њ—А–µ–є –Є —В.–і. –Я—А–Є—ЗвХ¶–Љ, —Н—В–Њ —В–µ–ї–Њ –і–Њ–ї–ґ–љ–Њ –Њ–њ–Є—Б—Л–≤–∞—В—М—Б—П –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –њ—А–Њ—Б—В—Л–Љ–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ–Є —Д–Њ—А–Љ—Г–ї–∞–Љ–Є –Є, –Ї—А–Њ–Љ–µ —В–Њ–≥–Њ, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Е–Њ—А–Њ—И–Њ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞—В—М —Д–Є–Ј–Є—З–µ—Б–Ї—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л.
–Э–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є
–Ю–±—Й–µ–њ—А–Є–Ј–љ–∞–љ–љ–Њ, —З—В–Њ –љ–∞–Є–±–Њ–ї–µ–µ —Г–і–Њ–±–љ—Л–Љ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —В–µ–ї–Њ–Љ –і–ї—П –Љ–Њ–і–µ–ї–Є –Ч–µ–Љ–ї–Є —П–≤–ї—П–µ—В—Б—П –Њ–±—Й–µ–Ј–µ–Љ–љ–Њ–є —Н–ї–ї–Є–њ—Б–Њ–Є–і (–Ю–Ч–≠) вИЪ —Г—А–Њ–≤–µ–љ–љ—Л–є —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П. –Х–≥–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї (–њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є!)
U(r
,q
) –љ–∞–Ј—Л–≤–∞—О—В –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞–Љ. –£—Б–ї–Њ–≤–Є–µ –і–ї—П –≤—Л–±–Њ—А–∞ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є:
- –¶–µ–љ—В—А –Љ–∞—Б—Б –Є –Њ—Б—М –≤—А–∞—Й–µ–љ–Є—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є —Б–Њ–≤–њ–∞–і–∞—О—В —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б –Є –Њ—Б—М—О –≤—А–∞—Й–µ–љ–Є—П —А–µ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є.
- –£–≥–ї–Њ–≤–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є —А–µ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є —Б–Њ–≤–њ–∞–і–∞—О—В.
- –Ь–∞—Б—Б–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —А–∞–≤–љ–∞ –Љ–∞—Б—Б–µ –Ч–µ–Љ–ї–Є.
- –Ч–Њ–љ–∞–ї—М–љ—Л–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤—В–Њ—А–Њ–є —Б—В–µ–њ–µ–љ–Є —А–µ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є —А–∞–≤–µ–љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ—Г –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є.
–Ю–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є –Љ—Л –±—Г–і–µ–Љ –Њ—В–Љ–µ—З–∞—В—М –≤–µ—А—Е–љ–Є–Љ –Є–ї–Є –љ–Є–ґ–љ–Є–Љ –Є–љ–і–µ–Ї—Б–Њ–Љ вМ†0вЦ†.
–Ш—В–∞–Ї, –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є —А–µ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є –Є–Љ–µ–µ—В –≤–Є–і
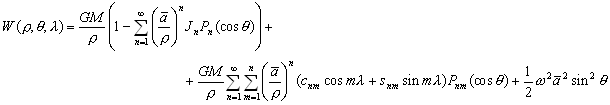 (6.1)
(6.1)
–≥–і–µ
 - —Б—А–µ–і–љ–Є–є —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ—Л–є —А–∞–і–Є—Г—Б –Ч–µ–Љ–ї–Є. –£—З–Є—В—Л–≤–∞—П, —З—В–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П —Б–Њ–і–µ—А–ґ–Є—В —В–Њ–ї—М–Ї–Њ –Ј–Њ–љ–∞–ї—М–љ—Л–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
- —Б—А–µ–і–љ–Є–є —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ—Л–є —А–∞–і–Є—Г—Б –Ч–µ–Љ–ї–Є. –£—З–Є—В—Л–≤–∞—П, —З—В–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П —Б–Њ–і–µ—А–ґ–Є—В —В–Њ–ї—М–Ї–Њ –Ј–Њ–љ–∞–ї—М–љ—Л–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
 (6.2)
(6.2)
–£—Б–ї–Њ–≤–Є–µ –і–ї—П –≤—Л–±–Њ—А–∞ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є :

–≠—В–Є —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞ –њ–Њ–і–ї–µ–ґ–∞—В —Г—В–Њ—З–љ–µ–љ–Є—О, –њ–Њ –Љ–µ—А–µ –љ–∞–Ї–Њ–њ–ї–µ–љ–Є—П –љ–Њ–≤—Л—Е –і–∞–љ–љ—Л—Е. –Р—Б—В—А–Њ–љ–Њ–Љ–Њ-–≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –љ—Г–ґ–і–∞—О—В—Б—П –≤ –µ–і–Є–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е. –Ґ–∞–Ї–∞—П —Б–Є—Б—В–µ–Љ–∞ –Њ–±—Л—З–љ–Њ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В—Б—П –љ–∞ –Ї—А—Г–њ–љ—Л—Е –Љ–µ–ґ–і—Г–љ–∞—А–Њ–і–љ—Л—Е —Б–Њ–±—А–∞–љ–Є—П—Е —Г—ЗвХ¶–љ—Л—Е. –Э–∞ –У–µ–љ–µ—А–∞–ї—М–љ–Њ–є –Р—Б—Б–∞–Љ–±–ї–µ–µ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ–Њ–≥–Њ –Р—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –°–Њ—О–Ј–∞ (–Ь–Р–°) –≤ 1976 –≥ –њ—А–Є–љ—П—В–Њ
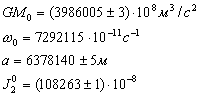
–Э–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–Њ–Ј–ґ–µ –Љ—Л –і–Њ–Ї–∞–ґ–µ–Љ –Ј–∞–Љ–µ—З–∞—В–µ–ї—М–љ—Г—О —В–µ–Њ—А–µ–Љ—Г –°—В–Њ–Ї—Б–∞, –Ї–Њ—В–Њ—А–∞—П —Г—В–≤–µ—А–ґ–і–∞–µ—В, —З—В–Њ, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –њ–ї–∞–љ–µ—В—Л, —П–≤–ї—П—О—Й–∞—П—Б—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П, –Ї–Њ—В–Њ—А–∞—П –Њ—Е–≤–∞—В—Л–≤–∞–µ—В –≤—Б–µ –Љ–∞—Б—Б—Л, –Є–Ј–≤–µ—Б—В–љ–∞ —В–∞–Ї–ґ–µ –њ–ї–∞–љ–µ—В–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–∞—П –њ–Њ—Б—В–Њ—П–љ–љ–∞—П
GM –Є —Г–≥–ї–Њ–≤–∞—П —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П w
, —В–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–µ –њ–Њ–ї–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ –≤–Њ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ. –І–Є—Б–ї–Њ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, –Њ–њ—А–µ–і–µ–ї—П—О—Й–Є—Е —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П —А–∞–≤–љ–Њ –і–≤—Г–Љ (–±–Њ–ї—М—И–∞—П –Є –Љ–∞–ї–∞—П –њ–Њ–ї—Г–Њ—Б–Є). –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –≤—Б–µ–≥–Њ –љ–∞–Љ –љ—Г–ґ–љ–Њ –Ј–љ–∞—В—М —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞, –Њ—Б—В–∞–ї—М–љ—Л–µ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —З–µ—А–µ–Ј –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї—Г—О –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Г—О –њ–Њ—Б—В–Њ—П–љ–љ—Г—О, —Г–≥–ї–Њ–≤—Г—О —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П, –±–Њ–ї—М—И—Г—О –њ–Њ–ї—Г–Њ—Б—М –Є —Б–ґ–∞—В–Є–µ –њ–ї–∞–љ–µ—В—Л. –Т —Д–Њ—А–Љ—Г–ї—Г (6.2) –≤—Е–Њ–і—П—В –±–µ—Б—З–Є—Б–ї–µ–љ–љ–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. –Ю–і–љ–∞–Ї–Њ —В–µ–Њ—А–Є—П –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, –≤—Б–µ —Б—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —З–µ—А–µ–Ј —Г–ґ–µ —Г–њ–Њ–Љ—П–љ—Г—В—Л–µ —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М
 –і–ї—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —Д–Є–≥—Г—А —Г–±—Л–≤–∞–µ—В –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±—Л—Б—В—А–Њ, —З–∞—Б—В–Њ –≤ —Д–Њ—А–Љ—Г–ї–µ (6.2) –і–ї—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Њ–≥—А–∞–љ–Є—З–Є–≤–∞—О—В—Б—П —В–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л–Љ —З–ї–µ–љ–Њ–Љ —Б—Г–Љ–Љ—Л. –Ґ–Њ–≥–і–∞ –љ–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
–і–ї—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —Д–Є–≥—Г—А —Г–±—Л–≤–∞–µ—В –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±—Л—Б—В—А–Њ, —З–∞—Б—В–Њ –≤ —Д–Њ—А–Љ—Г–ї–µ (6.2) –і–ї—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Њ–≥—А–∞–љ–Є—З–Є–≤–∞—О—В—Б—П —В–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л–Љ —З–ї–µ–љ–Њ–Љ —Б—Г–Љ–Љ—Л. –Ґ–Њ–≥–і–∞ –љ–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
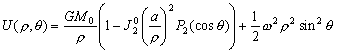 (6.3)
(6.3)
–Ю—В–±—А–∞—Б—Л–≤–∞–љ–Є–µ –Љ–∞–ї—Л—Е —З–ї–µ–љ–Њ–≤ –≤ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є–≤–Њ–і–Є—В –Ї —В–Њ–Љ—Г, —З—В–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М
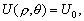 –≥–і–µ
–≥–і–µ  вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, —Г–ґ–µ –њ–µ—А–µ—Б—В–∞вХ¶—В, —Б—В—А–Њ–≥–Њ –≥–Њ–≤–Њ—А—П, –±—Л—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ. –Ґ–∞–Ї—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –±–ї–Є–Ј–Ї—Г—О –Ї —Б—Д–µ—А–µ, –љ–∞–Ј—Л–≤–∞—О—В —Б—Д–µ—А–Њ–Є–і–Њ–Љ.
вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, —Г–ґ–µ –њ–µ—А–µ—Б—В–∞вХ¶—В, —Б—В—А–Њ–≥–Њ –≥–Њ–≤–Њ—А—П, –±—Л—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ. –Ґ–∞–Ї—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –±–ї–Є–Ј–Ї—Г—О –Ї —Б—Д–µ—А–µ, –љ–∞–Ј—Л–≤–∞—О—В —Б—Д–µ—А–Њ–Є–і–Њ–Љ.
–Я–µ—А–µ–њ–Є—И–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ
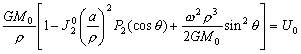 (6.4)
(6.4)
–Т–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ
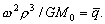 –§–Њ—А–Љ—Г–ї–∞ (6.4) —В–µ–њ–µ—А—М –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
–§–Њ—А–Љ—Г–ї–∞ (6.4) —В–µ–њ–µ—А—М –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
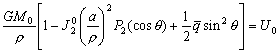 .
.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
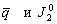 - –Љ–∞–ї—Л–µ –≤–µ–ї–Є—З–Є–љ—Л, —Г—А–∞–≤–љ–µ–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М —В–∞–Ї
- –Љ–∞–ї—Л–µ –≤–µ–ї–Є—З–Є–љ—Л, —Г—А–∞–≤–љ–µ–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М —В–∞–Ї
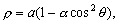 (6.5)
(6.5)
–У–і–µ a
=(a-b)/a - —Б–ґ–∞—В–Є–µ –њ–ї–∞–љ–µ—В—Л. –Я—А–µ–љ–µ–±—А–µ–≥–∞—П –≤–µ–ї–Є—З–Є–љ–∞–Љ–Є –њ–Њ—А—П–і–Ї–∞  , —Г—А–∞–≤–љ–µ–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ (6.4) –Љ–Њ–ґ–љ–Њ —Г–њ—А–Њ—Б—В–Є—В—М. –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
, —Г—А–∞–≤–љ–µ–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ (6.4) –Љ–Њ–ґ–љ–Њ —Г–њ—А–Њ—Б—В–Є—В—М. –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
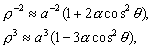
—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
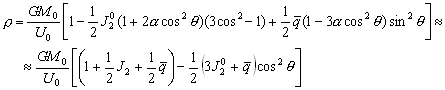
–°—А–∞–≤–љ–Є–≤–∞—П –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ —Б (6.5), –њ–Њ–ї—Г—З–Є–Љ
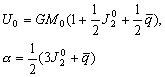 (6.6)
(6.6)
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Б–ґ–∞—В–Є–µ —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–є –њ–ї–∞–љ–µ—В—Л –Ј–∞–≤–Є—Б–Є—В –Њ—В —Б—В–Њ–Ї—Б–Њ–≤–Њ–є –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є
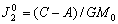 –Є –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–Њ–є —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П
–Є –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ–Њ–є —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П 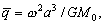 –Ї–Њ—В–Њ—А–∞—П –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: —Н—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ –Ї –≤–µ–ї–Є—З–Є–љ–µ, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±–ї–Є–Ј–Ї–Њ–є –Ї —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ. –Ґ–∞–Ї–Њ–є –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л–є —Б—Д–µ—А–Њ–Є–і –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ –Ъ–ї–µ—А–Њ, –њ–Њ –Є–Љ–µ–љ–Є —Д—А–∞–љ—Ж—Г–Ј—Б–Ї–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ , —А–∞–±–Њ—В–∞–≤—И–µ–≥–Њ –љ–∞–і —В–µ–Њ—А–Є–µ–є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —Д–Є–≥—Г—А –њ–ї–∞–љ–µ—В.
–Ї–Њ—В–Њ—А–∞—П –Є–Љ–µ–µ—В –њ—А–Њ—Б—В–Њ–є —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї: —Н—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–є —Б–Є–ї—Л –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ –Ї –≤–µ–ї–Є—З–Є–љ–µ, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±–ї–Є–Ј–Ї–Њ–є –Ї —Б–Є–ї–µ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ. –Ґ–∞–Ї–Њ–є –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л–є —Б—Д–µ—А–Њ–Є–і –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ —Б—Д–µ—А–Њ–Є–і–∞ –Ъ–ї–µ—А–Њ, –њ–Њ –Є–Љ–µ–љ–Є —Д—А–∞–љ—Ж—Г–Ј—Б–Ї–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ , —А–∞–±–Њ—В–∞–≤—И–µ–≥–Њ –љ–∞–і —В–µ–Њ—А–Є–µ–є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Л—Е —Д–Є–≥—Г—А –њ–ї–∞–љ–µ—В.
–°–ґ–∞—В–Є–µ –і–ї—П —Б—Д–µ—А–Њ–Є–і–∞ –Ъ–ї–µ—А–Њ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –Є —В–∞–Ї
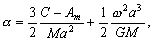
–≥–і–µ
 —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–Ј –і–≤—Г—Е —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ—Л—Е –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Є–љ–µ—А—Ж–Є–Є. –І–µ—В—Л—А—М–Љ—П —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є , –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —П–≤–ї—П—О—В—Б—П
—Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Є–Ј –і–≤—Г—Е —Н–Ї–≤–∞—В–Њ—А–Є–∞–ї—М–љ—Л—Е –Љ–Њ–Љ–µ–љ—В–Њ–≤ –Є–љ–µ—А—Ж–Є–Є. –І–µ—В—Л—А—М–Љ—П —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є , –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —П–≤–ї—П—О—В—Б—П 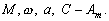
–Я—А–Є –≤—Л–≤–Њ–і–µ —Д–Њ—А–Љ—Г–ї—Л –і–ї—П —Б–ґ–∞—В–Є—П –њ–ї–∞–љ–µ—В—Л –Љ—Л –љ–µ –њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є—Б—М –љ–Є–Ї–∞–Ї–Є–Љ–Є –≥–Є–њ–Њ—В–µ–Ј–∞–Љ–Є –Њ –µвХ¶ —Б—В—А–Њ–µ–љ–Є–Є. –Ъ–ї–µ—А–Њ –ґ–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–ї –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ—Г—О –Љ–Њ–і–µ–ї—М, –њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –Љ–∞—Б—Б—Л —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л –≤ –≤–Є–і–µ —В–Њ–љ–Ї–Є—Е —Б—Д–µ—А–Њ–Є–і–∞–ї—М–љ—Л—Е —Б–ї–ЊвХ¶–≤. –Ш–Љ –њ–Њ—Б—В—А–Њ–µ–љ–∞ –љ–µ —В–Њ–ї—М–Ї–Њ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М —Б–ґ–∞—В–Є—П –њ–ї–∞–љ–µ—В—Л –Њ—В –µвХ¶ —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П, –љ–Њ –Є —Б–ґ–∞—В–Є–Є –≤–љ—Г—В—А–µ–љ–љ–Є—Е —Б–ї–ЊвХ¶–≤. –Я–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ —Н—В–Є —Б–ґ–∞—В–Є—П —Г–Љ–µ–љ—М—И–∞—О—В—Б—П –њ–Њ –Љ–µ—А–µ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є—П –Ї —Ж–µ–љ—В—А—Г –њ–ї–∞–љ–µ—В—Л.
–Ю—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –Ј–∞–Ї–Њ–љ –Є–Ј–Љ–µ–љ–µ–љ–Є—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є —Б —И–Є—А–Њ—В–Њ–є –љ–∞ —Б—Д–µ—А–Њ–Є–і–µ –Ъ–ї–µ—А–Њ —В–∞–Ї–ґ–µ —Б —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ —Б–ґ–∞—В–Є—П. –Ш–Ј —Д–Њ—А–Љ—Г–ї—Л (6.3) —Б–ї–µ–і—Г–µ—В
–°–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н–Ї–≤–∞—В–Њ—А–µ
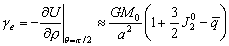
–°–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–ї—О—Б–µ
 .
.
–Ю—В–љ–Њ—И–µ–љ–Є–µ
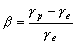 –Є–љ–Њ–≥–і–∞ –љ–∞–Ј—Л–≤–∞—О—В –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–µ —Б–ґ–∞—В–Є–µ. –Ш–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї —Б–ї–µ–і—Г–µ—В:
–Є–љ–Њ–≥–і–∞ –љ–∞–Ј—Л–≤–∞—О—В –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–µ —Б–ґ–∞—В–Є–µ. –Ш–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї —Б–ї–µ–і—Г–µ—В:

–Ґ–µ–Њ—А–µ–Љ–∞ –Ъ–ї–µ—А–Њ
. –≠—В–∞ —В–µ–Њ—А–µ–Љ–∞ —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В —Б–≤—П–Ј—М –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ –Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П —Б —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В—М—О –≤—А–∞—Й–µ–љ–Є—П –њ–ї–∞–љ–µ—В—Л. –Ш–Ј –њ—А–Є–≤–µ–і–µ–љ–љ—Л—Е —Д–Њ—А–Љ—Г–ї —Б–ї–µ–і—Г–µ—В, —З—В–Њ
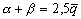
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ —Б—Г–Љ–Љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ –Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П –≤ –њ–µ—А–≤–Њ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–Є –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –≤—В–Њ—А–Њ–≥–Њ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞
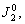 –∞ –Ј–∞–≤–Є—Б–Є—В –ї–Є—И—М –Њ—В
–∞ –Ј–∞–≤–Є—Б–Є—В –ї–Є—И—М –Њ—В 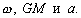
–Ґ–µ–Њ—А–µ–Љ–∞ –°—В–Њ–Ї—Б–∞
. –≠—В–∞ —В–µ–Њ—А–µ–Љ–∞ –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –µ–і–Є–љ—Б—В–≤–µ–љ–љ–Њ—Б—В—М –≤–љ–µ—И–љ–µ–є –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є —В–µ–Њ—А–Є–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –µ—Б–ї–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–µ —В–µ–ї–Њ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –≤—А–∞—Й–∞–µ—В—Б—П —Б –Є–Ј–≤–µ—Б—В–љ–Њ–є —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В—М—О, –µ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, —П–≤–ї—П—О—Й–∞—П—Б—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П, –Ї–Њ—В–Њ—А–∞—П –Њ—Е–≤–∞—В—Л–≤–∞–µ—В –≤—Б—О –Љ–∞—Б—Б—Г, —В–∞–Ї–ґ–µ –Є–Ј–≤–µ—Б—В–љ–∞, —В–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –Є –µ–≥–Њ –њ–µ—А–≤—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –±—Г–і—Г—В –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ—Л –Ї–∞–Ї –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S, —В–∞–Ї –Є –≤–Њ –≤—БвХ¶–Љ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ.
–Ґ–µ–Њ—А–µ–Љ–∞ –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –Њ—В –њ—А–Њ—В–Є–≤–љ–Њ–≥–Њ. –Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –і–≤–∞ —А–∞–Ј–ї–Є—З–љ—Л—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є
 , –Ї–Њ—В–Њ—А—Л–µ –њ—А–Є–љ–Є–Љ–∞—О—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ
, –Ї–Њ—В–Њ—А—Л–µ –њ—А–Є–љ–Є–Љ–∞—О—В –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ 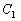 –Є
–Є 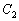 . –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,
. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, 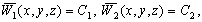 –≥–і–µ —З–µ—А—В–∞ —Б–≤–µ—А—Е—Г –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –Њ—В–љ–Њ—Б—П—В—Б—П –Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S .–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –µ—Б—В—М —Б—Г–Љ–Љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–≥–Њ—В–µ–љ–Є—П –Є —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, —В–Њ
–≥–і–µ —З–µ—А—В–∞ —Б–≤–µ—А—Е—Г –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –Њ—В–љ–Њ—Б—П—В—Б—П –Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S .–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –µ—Б—В—М —Б—Г–Љ–Љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–≥–Њ—В–µ–љ–Є—П –Є —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, —В–Њ
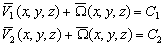 .
.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ —А–∞–Ј–љ–Њ—Б—В—М
 –Я–Њ–ї—Г—З–µ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, —В–∞–Ї –Ї–∞–Ї –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–∞—П –≤–Њ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞.
–Я–Њ–ї—Г—З–µ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, —В–∞–Ї –Ї–∞–Ї –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–∞—П –≤–Њ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞.
–Я—А–Є–Љ–µ–љ–Є–Љ –њ–µ—А–≤—Г—О —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞ (—Б–Љ. –ї–µ–Ї—Ж–Є—О 3)
–і–ї—П —Б–ї—Г—З–∞—П, –Ї–Њ–≥–і–∞ U=T –Є V=T. –Т—Л–±–µ—А–µ–Љ, –≤ –Ї–∞—З–µ—Б—В–≤–µ вМ†—В–µ–ї–∞вЦ† –њ–Њ –Ї–Њ—В–Њ—А–Њ–Љ—Г –љ—Г–ґ–љ–Њ –≤—Л–њ–Њ–ї–љ–Є—В—М –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ вИЪ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –ї–µ–ґ–∞—Й–µ–µ –Љ–µ–ґ–і—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О S –Є —Б—Д–µ—А–Њ–є S
—Б –Њ—З–µ–љ—М –±–Њ–ї—М—И–Є–Љ —А–∞–і–Є—Г—Б–Њ–Љ, —В–∞–Ї —З—В–Њ–±—Л –љ–∞—И–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –±—Л–ї–∞ —Ж–µ–ї–Є–Ї–Њ–Љ –≤–љ—Г—В—А–Є —Б—Д–µ—А—Л. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —Н—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ —З–µ—А–µ–Ј SS
. –Ґ–µ–њ–µ—А—М –њ–µ—А–≤–∞—П —Д–Њ—А–Љ—Г–ї–∞ –У—А–Є–љ–∞ –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
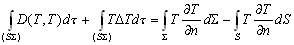 . (6.7)
. (6.7)
–Ч–љ–∞–Ї –Љ–Є–љ—Г—Б –Љ–µ–ґ–і—Г –Є–љ—В–µ–≥—А–∞–ї–∞–Љ–Є –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –њ–Њ–ї—Г—З–µ–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї—Л –Њ–Ј–љ–∞—З–∞–µ—В –ї–Є—И—М —В–Њ, —З—В–Њ –≤–љ–µ—И–љ—П—П –љ–Њ—А–Љ–∞–ї—М –і–ї—П –Њ–і–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —П–≤–ї—П–µ—В—Б—П –≤–љ—Г—В—А–µ–љ–љ–µ–є –і–ї—П –і—А—Г–≥–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ–Њ—Б–ї–µ–і–љ–Є–є –Є–љ—В–µ–≥—А–∞–ї. –§—Г–љ–Ї—Ж–Є—П
T(x,y,z) –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S - –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞, —А–∞–≤–љ–∞—П 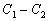 , –њ–Њ—Н—В–Њ–Љ—Г
, –њ–Њ—Н—В–Њ–Љ—Г
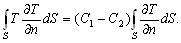
–Ю–і–љ–∞–Ї–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Д—Г–љ–Ї—Ж–Є—П –Ґ —П–≤–ї—П–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є, –Є–љ—В–µ–≥—А–∞–ї –њ–Њ –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ—В –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є, —Б–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ –Њ –њ–Њ—В–Њ–Ї–µ (—Б–Љ. –ї–µ–Ї—Ж–Є—О 3), —А–∞–≤–µ–љ –љ—Г–ї—О.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–µ–њ–µ—А—М –≤—В–Њ—А–Њ–є –Є–љ—В–µ–≥—А–∞–ї –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є –≤—Л—А–∞–ґ–µ–љ–Є—П (6.7). –Я—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ –љ–Њ—А–Љ–∞–ї–Є –Ї —Б—Д–µ—А–µ –µ—Б—В—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ–∞—П –њ–Њ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А—Г. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –і–ї—П –Њ—З–µ–љ—М –±–Њ–ї—М—И–Њ–≥–Њ —А–∞–і–Є—Г—Б–∞ –Є—Б—Е–Њ–і–љ–Њ–µ —В–µ–ї–Њ –Љ–Њ–ґ–љ–Њ —Б—З–Є—В–∞—В—М –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Њ–є, —В–Њ
T@
A/R. –Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ 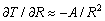 , –≥–і–µ –Р вИЪ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В
, –≥–і–µ –Р вИЪ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В
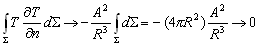
–Т –ї–µ–≤–Њ–є —З–∞—Б—В–Є —А–∞–≤–µ–љ—Б—В–≤–∞ (6.7) –љ—Г–ґ–љ–Њ –њ–Њ–ї–Њ–ґ–Є—В—М
 , —В–∞–Ї –Ї–∞–Ї –Ґ(x,y,z) вИЪ —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, –њ–Њ—Н—В–Њ–Љ—Г —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
, —В–∞–Ї –Ї–∞–Ї –Ґ(x,y,z) вИЪ —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, –њ–Њ—Н—В–Њ–Љ—Г —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
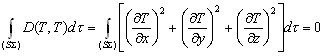
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л–Љ –љ–Є –њ—А–Є –Ї–∞–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В, –Њ—Б—В–∞вХ¶—В—Б—П —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і, —З—В–Њ –Ґ вИЪ–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ –≤–Њ –≤—БвХ¶–Љ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ. –Э–Њ –љ–∞ —Б—Д–µ—А–µ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –±–Њ–ї—М—И–Є–Љ —А–∞–і–Є—Г—Б–Њ–Љ –Њ–љ–∞ —А–∞–≤–љ–∞ –љ—Г–ї—О –Є –≤ —Б–Є–ї—Г –љ–µ–њ—А–µ—А—Л–≤–љ–Њ—Б—В–Є –Њ–љ–∞ —А–∞–≤–љ–∞ –љ—Г–ї—О –Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є
S. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ T(x,y,z)=0 –≤–Њ –≤—Б–µ–Љ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, —В–Њ –µ—Б—В—М 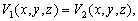 —З—В–Њ –Є –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В —В–µ–Њ—А–µ–Љ—Г.
—З—В–Њ –Є –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В —В–µ–Њ—А–µ–Љ—Г.
–У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞ —Г—А–Њ–≤–µ–љ–љ–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –µ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П. –£—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≤ –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Є–Љ–µ–µ—В –≤–Є–і
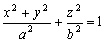 .
.
–Я–µ—А–µ–є–івХ¶–Љ –Ї –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В (—Б–Љ. –ї–µ–Ї—Ж–Є—О 2)
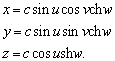
–Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є, —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П —Б –њ–Њ–ї—Г–Њ—Б—П–Љ–Є
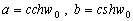 –Є–Љ–µ–µ—В –≤–Є–і
–Є–Љ–µ–µ—В –≤–Є–і 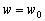 . –Ф–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞
. –Ф–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞
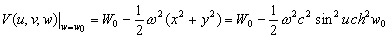
–Ш—В–∞–Ї, –љ–∞–Љ –Є–Ј–≤–µ—Б—В–µ–љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Ґ—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –µ–≥–Њ –≤–Њ –≤—БвХ¶–Љ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, –Њ–љ–∞ –њ–Њ–і—З–Є–љ—П–µ—В—Б—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞, –Ї–Њ—В–Њ—А–Њ–µ –Љ–Њ–ґ–љ–Њ –љ–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ
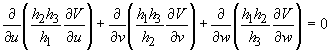 ,
,
–≥–і–µ
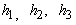 - –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ы–∞–Љ–µ. –Ю–њ—А–µ–і–µ–ї–Є–Љ –Є—Е
- –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ы–∞–Љ–µ. –Ю–њ—А–µ–і–µ–ї–Є–Љ –Є—Е
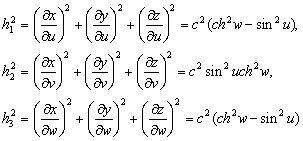 (6.8)
(6.8)
–Т—Л—З–Є—Б–ї–Є–Љ –Њ—В–љ–Њ—И–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Ы–∞–Љ–µ, —Б—В–Њ—П—Й–Є–µ –≤ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ —Г—А–∞–≤–љ–µ–љ–Є–Є –Ы–∞–њ–ї–∞—Б–∞
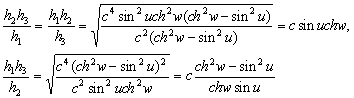 (6.9)
(6.9)
–Ш—В–∞–Ї, —Г—А–∞–≤–љ–µ–љ–Є–µ –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П —Д—Г–љ–Ї—Ж–Є–Є
V(u,v,w) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
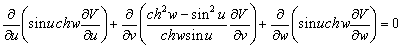 (6.10)
(6.10)
–Я–Њ–ї—Г—З–µ–љ–љ–Њ–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –ї–Є–љ–µ–є–љ–Њ, –њ–Њ—Н—В–Њ–Љ—Г –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М —А–µ—И–µ–љ–Є–µ –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є. –Т —Б–Є–ї—Г –Њ—Б–µ–≤–Њ–є —Б–Є–Љ–Љ–µ—В—А–Є–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П –Є —В–Њ–≥–Њ, —З—В–Њ –≥—А–∞–љ–Є—З–љ—Л–µ —Г—Б–ї–Њ–≤–Є—П –љ–µ –Ј–∞–≤–Є—Б—П—В –Њ—В –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є
v вИЪ –∞–љ–∞–ї–Њ–≥–∞ –і–Њ–ї–≥–Њ—В—Л, —В–Њ –Є —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П –љ–µ –і–Њ–ї–ґ–љ–Њ —Б–Њ–і–µ—А–ґ–∞—В—М —Н—В–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є –Є—Й–µ–Љ —А–µ—И–µ–љ–Є–µ –≤ –≤–Є–і–µ
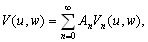
–≥–і–µ
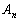 вИЪ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ, –Ї–Њ—В–Њ—А—Л–µ –љ—Г–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –Є–Ј –Ї—А–∞–µ–≤—Л—Е —Г—Б–ї–Њ–≤–Є–є, –∞
вИЪ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ, –Ї–Њ—В–Њ—А—Л–µ –љ—Г–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –Є–Ј –Ї—А–∞–µ–≤—Л—Е —Г—Б–ї–Њ–≤–Є–є, –∞ 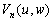 вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞
вИЪ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є, —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞
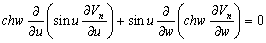 (6.11)
(6.11)
–Ъ–∞–Ї –Є –≤ —Б–ї—Г—З–∞–µ —А–µ—И–µ–љ–Є—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –і–ї—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є, –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М —А–µ—И–µ–љ–Є–µ –≤ –≤–Є–і–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е —Д—Г–љ–Ї—Ж–Є–є, –Ї–∞–ґ–і–∞—П –Є–Ј –Ї–Њ—В–Њ—А—Л—Е —П–≤–ї—П–µ—В—Б—П —Д—Г–љ–Ї—Ж–Є–µ–є –Њ–і–љ–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є
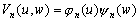 (6.12)
(6.12)
–Я–Њ–і—Б—В–∞–≤–Є–Љ —А–µ—И–µ–љ–Є–µ, –Ј–∞–і–∞–љ–љ–Њ–µ –≤ –≤–Є–і–µ (6.12) –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ (6.11) –Є –њ–Њ–і–µ–ї–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–∞
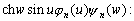
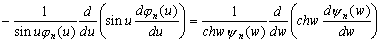 .
.
–Я–Њ–ї—Г—З–µ–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ –њ—А–Є –ї—О–±—Л—Е –Ј–љ–∞—З–µ–љ–Є—П—Е –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е. –≠—В–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –ї–Є—И—М –≤ —В–Њ–Љ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –Њ–±–µ —З–∞—Б—В–Є —Н—В–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П —А–∞–≤–љ—Л –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ —Н—В—Г –њ–Њ—Б—В–Њ—П–љ–љ—Г—О —З–µ—А–µ–Ј
k. –Я–Њ–ї—Г—З–Є–Љ –і–≤–∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є—П
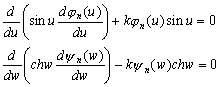 (6.13)
(6.13)
–Я–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ –њ–µ—А–≤–Њ–µ –Є–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е –Ј–і–µ—Б—М —Г—А–∞–≤–љ–µ–љ–Є–є –њ—А–Є
k=n(n+1) –µ—Б—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ –і–ї—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ (—Б–Љ. –ї–µ–Ї—Ж–Є—О 3), —В–Њ –µ—Б—В—М
 (6.14)
(6.14)
–Я–Њ–ї–Њ–ґ–Є–Љ
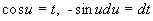 , —В–Њ–≥–і–∞ –≤–Љ–µ—Б—В–Њ –њ–µ—А–≤–Њ–≥–Њ –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є–є (6.13) –±—Г–і–µ–Љ –Є–Љ–µ—В—М
, —В–Њ–≥–і–∞ –≤–Љ–µ—Б—В–Њ –њ–µ—А–≤–Њ–≥–Њ –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є–є (6.13) –±—Г–і–µ–Љ –Є–Љ–µ—В—М
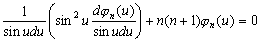
–Є–ї–Є
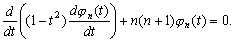 (6.15)
(6.15)
–£—А–∞–≤–љ–µ–љ–Є–µ (6.15) —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –і–ї—П –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ (—Б–Љ. –ї–µ–Ї—Ж–Є—О 3, —Д–Њ—А–Љ—Г–ї–∞ (3.23))
–Ш—В–∞–Ї, —А–µ—И–µ–љ–Є–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞ –≤ –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –±—Г–і–µ—В —Д—Г–љ–Ї—Ж–Є—П
 , (6.16)
, (6.16)
–Ї–Њ—В–Њ—А–∞—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –Ј–љ–∞—З–µ–љ–Є—П
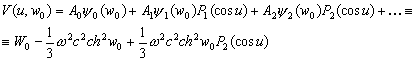 (6.17)
(6.17)
–Я—А–Є –≤—Л–≤–Њ–і–µ —Д–Њ—А–Љ—Г–ї—Л (6.17) –Љ—Л –њ—А–Є–љ—П–ї–Є –≤–Њ –≤–љ–Є–Љ–∞–љ–Є–µ, —З—В–Њ
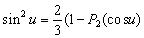 . –°—А–∞–≤–љ–Є–≤–∞—П –ї–µ–≤—Г—О –Є –њ—А–∞–≤—Г—О —З–∞—Б—В–Є —Д–Њ—А–Љ—Г–ї—Л (6,17) –Љ—Л –њ—А–Є—Е–Њ–і–Є–Љ –Ї –≤—Л–≤–Њ–і—Г, —З—В–Њ
. –°—А–∞–≤–љ–Є–≤–∞—П –ї–µ–≤—Г—О –Є –њ—А–∞–≤—Г—О —З–∞—Б—В–Є —Д–Њ—А–Љ—Г–ї—Л (6,17) –Љ—Л –њ—А–Є—Е–Њ–і–Є–Љ –Ї –≤—Л–≤–Њ–і—Г, —З—В–Њ
 (6.18)
(6.18)
–Ш—В–∞–Ї, –≤ —Д–Њ—А–Љ—Г–ї–µ (6.16) –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Њ—В–ї–Є—З–љ—Л–µ –Њ—В –љ—Г–ї—П —В–Њ–ї—М–Ї–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л
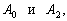 –њ–Њ—Н—В–Њ–Љ—Г —Б—В—А–Њ–≥–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤ –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ
–њ–Њ—Н—В–Њ–Љ—Г —Б—В—А–Њ–≥–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤ –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ
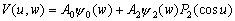 . (6.19)
. (6.19)
–Ю—Б—В–∞вХ¶—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М —Д—Г–љ–Ї—Ж–Є–Є
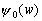 –Є
–Є 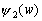 . –Ъ–∞–Ї —Б–ї–µ–і—Г–µ—В –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є–є (6.13), —Д—Г–љ–Ї—Ж–Є—О
. –Ъ–∞–Ї —Б–ї–µ–і—Г–µ—В –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є–є (6.13), —Д—Г–љ–Ї—Ж–Є—О 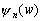 –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М, —А–µ—И–Є–≤ –≤—В–Њ—А–Њ–µ –Є–Ј –љ–∞–Ј–≤–∞–љ–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –њ—А–Є –Ї=0 –Є –њ—А–Є –Ї=6 (–Ї=–њ(–њ+1)):
–Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М, —А–µ—И–Є–≤ –≤—В–Њ—А–Њ–µ –Є–Ј –љ–∞–Ј–≤–∞–љ–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –њ—А–Є –Ї=0 –Є –њ—А–Є –Ї=6 (–Ї=–њ(–њ+1)):
 (6.20)
(6.20)
–Я–Њ–ї—Г—З–µ–љ–љ—Л–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є—П–Љ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В —Д—Г–љ–Ї—Ж–Є–Є
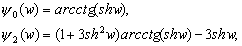
–≤ —ЗвХ¶–Љ –Љ–Њ–ґ–љ–Њ —Г–±–µ–і–Є—В—Б—П –њ—А–Њ—Б—В–Њ–є –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–Њ–є –≤ —Г—А–∞–≤–љ–µ–љ–Є—П (6.20).
–Ш–Ј–±–∞–≤–Є–Љ—Б—П —В–µ–њ–µ—А—М –Њ—В –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є, –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е –љ–∞–Љ–Є –њ—А–Є —А–µ—И–µ–љ–Є–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –Ъ–∞–Ї –Љ—Л —Г–ґ–µ –≥–Њ–≤–Њ—А–Є–ї–Є, –њ–µ—А–µ–Љ–µ–љ–љ–∞—П
w –Њ–њ—А–µ–і–µ–ї—П–µ—В —Б–µ–Љ–µ–є—Б—В–≤–Њ —Б–Њ—Д–Њ–Ї—Г—Б–љ—Л—Е —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–≤. –Т–Њ–Ј—М–ЉвХ¶–Љ –љ–µ–Ї–Њ—В–Њ—А—Г—О —В–Њ—З–Ї—Г –љ–∞ –Њ—Б–Є –≤—А–∞—Й–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –љ–∞—Е–Њ–і—П—Й—Г—О—Б—П –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є d –Њ—В —Ж–µ–љ—В—А–∞. –Ґ–Њ–≥–і–∞ –і–ї—П —Н—В–Њ–є —В–Њ—З–Ї–Є u=0, w=arcsh(d/c). –Ч–∞–Љ–µ–љ–Є–Љ –њ–µ—А–µ–Љ–µ–љ–љ—Г—О w –љ–∞ arcsh(d/c):
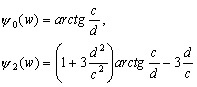 (6.21)
(6.21)
–Ш—В–∞–Ї, –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–є —В–Њ—З–Ї–µ –† –≤–љ–µ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Є–Љ–µ–µ—В –≤–Є–і
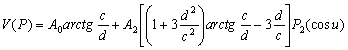 (6.22)
(6.22)
–Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л
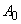 –Є
–Є 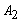 –Њ–њ—А–µ–і–µ–ї–Є–Љ –Є–Ј –Ї—А–∞–µ–≤–Њ–≥–Њ —Г—Б–ї–Њ–≤–Є—П
–Њ–њ—А–µ–і–µ–ї–Є–Љ –Є–Ј –Ї—А–∞–µ–≤–Њ–≥–Њ —Г—Б–ї–Њ–≤–Є—П
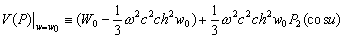
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
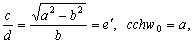 –њ–Њ—Б–ї–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –њ–Њ–ї—Г—З–Є–Љ
–њ–Њ—Б–ї–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–є –њ–Њ–ї—Г—З–Є–Љ
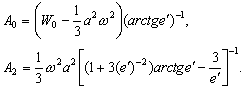 (6.23)
(6.23)
–§–Њ—А–Љ—Г–ї—Л (6.22) –Є (6.23) –Њ–њ—А–µ–і–µ–ї—П—О—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ—Л–Љ —В–µ–ї–Њ–Љ –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Є, –ї–µ–ґ–∞—Й–µ–є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б–Њ—Д–Њ–Ї—Г—Б–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞
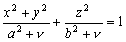
–Ч–љ–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є –†
(x,y,z) –Є –њ–Њ–ї—Г–Њ—Б–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ a –Є b –ї–µ–≥–Ї–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ–∞—А–∞–Љ–µ—В—Аn
, –∞ —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Є –Љ–∞–ї—Г—О –њ–Њ–ї—Г–Њ—Б—М 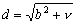 —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –њ—А–Њ—Е–Њ–і—П—Й–µ–≥–Њ —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г.
—Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –њ—А–Њ—Е–Њ–і—П—Й–µ–≥–Њ —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г.
–Ш–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е —Д–Њ—А–Љ—Г–ї –≤–Є–і–љ–Њ, —З—В–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Б–Њ–і–µ—А–ґ–Є—В –ї–Є—И—М —З–µ—В—Л—А–µ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–∞
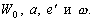 –≠—В–Є —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞ –∞–±—Б–Њ–ї—О—В–љ–Њ —Б—В—А–Њ–≥–Њ –Њ–њ—А–µ–і–µ–ї—П—О—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ—Л–Љ —В–µ–ї–Њ–Љ –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Є, –ї–µ–ґ–∞—Й–µ–є –≤–Њ –≤–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, –њ—А–Є –ї—О–±–Њ–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–Є –Љ–∞—Б—Б –≤–љ—Г—В—А–Є —В–µ–ї–∞ –ї–Є—И—М –±—Л –µ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Њ—Б—В–∞–≤–∞–ї–∞—Б—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П.
–≠—В–Є —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞ –∞–±—Б–Њ–ї—О—В–љ–Њ —Б—В—А–Њ–≥–Њ –Њ–њ—А–µ–і–µ–ї—П—О—В –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ—Л–Љ —В–µ–ї–Њ–Љ –Љ–∞—В–µ—А–Є–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Є, –ї–µ–ґ–∞—Й–µ–є –≤–Њ –≤–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ, –њ—А–Є –ї—О–±–Њ–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–Є –Љ–∞—Б—Б –≤–љ—Г—В—А–Є —В–µ–ї–∞ –ї–Є—И—М –±—Л –µ–≥–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Њ—Б—В–∞–≤–∞–ї–∞—Б—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П.
–°–≤—П–Ј—М –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П
—Б —З–µ—В—Л—А—М–Љ—П —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–Љ–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–Љ–Є.
–Я–Њ—В–µ–љ—Ж–Є–∞–ї —В–µ–ї–∞ –≤—А–∞—Й–µ–љ–Є—П –њ—А–Є –Њ—Б–µ–≤–Њ–є —Б–Є–Љ–Љ–µ—В—А–Є–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–∞—Б—Б –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –≤ –≤–Є–і–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ –Ј–Њ–љ–∞–ї—М–љ—Л–Љ –≥–∞—А–Љ–Њ–љ–Є–Ї–∞–Љ. –Ф–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ–µ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Н–Ї–≤–∞—В–Њ—А–∞ –Ї–∞–Ї –Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Б–Є–Љ–Љ–µ—В—А–Є–Є –њ—А–Є–≤–Њ–і–Є—В –Ї —В–Њ–Љ—Г, —З—В–Њ —Н—В–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –±—Г–і–µ—В –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ —В–Њ–ї—М–Ї–Њ —ЗвХ¶—В–љ—Л–Љ–Є –Ј–Њ–љ–∞–ї—М–љ—Л–Љ–Є –≥–∞—А–Љ–Њ–љ–Є–Ї–∞–Љ–Є:
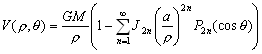 . (6.24)
. (6.24)
–ІвХ¶—В–љ–Њ—Б—В—М –≥–∞—А–Љ–Њ–љ–Є–Ї, –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, –љ–µ –Њ—З–µ–≤–Є–і–љ–∞. –Э–Њ –Њ–±—А–∞—В–Є–Љ—Б—П –Ї –Ј–і—А–∞–≤–Њ–Љ—Г —Б–Љ—Л—Б–ї—Г. –Х—Б–ї–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П вИЪ —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Н–Ї–≤–∞—В–Њ—А–∞ —В–µ–ї–Њ, —В–Њ –Є –Љ–∞—Б—Б—Л –µ–≥–Њ –і–Њ–ї–ґ–љ—Л –±—Л—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ. –Т –њ—А–Њ—В–Є–≤–љ–Њ–Љ —Б–ї—Г—З–∞–µ –≤–Њ–Ј–љ–Є–Ї–љ–µ—В вМ†–≥—А—Г—И–µ–≤–Є–і–љ–Њ—Б—В—МвЦ†, —З—В–Њ –њ—А–Є–≤–µ–івХ¶—В –Ї —В–Њ–Љ—Г, —З—В–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –њ–µ—А–µ—Б—В–∞–љ–µ—В –±—Л—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П. –С–Њ–ї–µ–µ –Ї–Њ—А—А–µ–Ї—В–љ—Л–µ —А–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –њ—А–Њ–≤–Њ–і—П—В—Б—П —Б –њ–Њ–Ј–Є—Ж–Є–Є —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А —А–∞–≤–љ–Њ–≤–µ—Б–Є—П –љ–µ–±–µ—Б–љ—Л—Е —В–µ–ї, –≤ –Ї–Њ—В–Њ—А–Њ–є —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ —Н–Ї–≤–∞—В–Њ—А–∞, –Ї–∞–Ї –њ–ї–Њ—Б–Ї–Њ—Б—В–Є —Б–Є–Љ–Љ–µ—В—А–Є–Є, –і–Њ–Ї–∞–Ј–∞–љ–Њ –≤–њ–Њ–ї–љ–µ —Б—В—А–Њ–≥–Њ.
–§–Њ—А–Љ—Г–ї–∞ (6.24) —Б–Њ–і–µ—А–ґ–Є—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–µ —З–Є—Б–ї–Њ –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, —Е–Њ—В—П –Є—Е –і–Њ–ї–ґ–љ–Њ –±—Л—В—М —В–Њ–ї—М–Ї–Њ —З–µ—В—Л—А–µ. –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л
 –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М —З–µ—А–µ–Ј –і—А—Г–≥–Є–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ. –Э–µ –±—Г–і–µ–Љ –њ—А–Є–≤–Њ–і–Є—В—М –Ј–і–µ—Б—М –і–Њ–≤–Њ–ї—М–љ–Њ –≥—А–Њ–Љ–Њ–Ј–і–Ї–Є—Е –≤—Л–Ї–ї–∞–і–Њ–Ї, –Ї–Њ—В–Њ—А—Л–µ –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –≤ –Ї–љ–Є–≥–µ –Ы.–Я.–Я–µ–ї–ї–Є–љ–µ–љ–∞ вМ†–Т—Л—Б—И–∞—П –≥–µ–Њ–і–µ–Ј–Є—ПвЦ† –Ь.–Э–µ–і—А–∞.1978. –Ґ–∞–Љ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ
–Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М —З–µ—А–µ–Ј –і—А—Г–≥–Є–µ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї—М–љ—Л–µ –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ. –Э–µ –±—Г–і–µ–Љ –њ—А–Є–≤–Њ–і–Є—В—М –Ј–і–µ—Б—М –і–Њ–≤–Њ–ї—М–љ–Њ –≥—А–Њ–Љ–Њ–Ј–і–Ї–Є—Е –≤—Л–Ї–ї–∞–і–Њ–Ї, –Ї–Њ—В–Њ—А—Л–µ –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –≤ –Ї–љ–Є–≥–µ –Ы.–Я.–Я–µ–ї–ї–Є–љ–µ–љ–∞ вМ†–Т—Л—Б—И–∞—П –≥–µ–Њ–і–µ–Ј–Є—ПвЦ† –Ь.–Э–µ–і—А–∞.1978. –Ґ–∞–Љ –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ
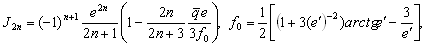
–≥–і–µ
e –Є  —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –њ–µ—А–≤—Л–є –Є –≤—В–Њ—А–Њ–є —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В—Л —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Э–∞–њ—А–Є–Љ–µ—А,
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –њ–µ—А–≤—Л–є –Є –≤—В–Њ—А–Њ–є —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В—Л —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Э–∞–њ—А–Є–Љ–µ—А,
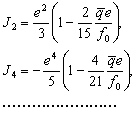
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤–µ–ї–Є—З–Є–љ–∞
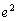 - –Љ–∞–ї–∞—П –њ–Њ—А—П–і–Ї–∞ —Б–ґ–∞—В–Є—П, —В–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л
- –Љ–∞–ї–∞—П –њ–Њ—А—П–і–Ї–∞ —Б–ґ–∞—В–Є—П, —В–Њ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л 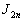 –і–ї—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —Г–±—Л–≤–∞—О—В —Б —А–Њ—Б—В–Њ–Љ –њ –Ї–∞–Ї —Б—В–µ–њ–µ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П
–і–ї—П –≥–Є–і—А–Њ—Б—В–∞—В–Є—З–µ—Б–Ї–Є —А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —Г–±—Л–≤–∞—О—В —Б —А–Њ—Б—В–Њ–Љ –њ –Ї–∞–Ї —Б—В–µ–њ–µ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П 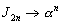 –Є–ї–Є
–Є–ї–Є 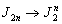 . –Ю—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В —Н—В–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞, –Ї–Њ—В–Њ—А–Њ–µ —З–∞—Б—В–Њ –Љ–Њ–ґ–љ–Њ –љ–∞–±–ї—О–і–∞—В—М –љ–∞ –њ—А–∞–Ї—В–Є–Ї–µ, –≥–Њ–≤–Њ—А–Є—В –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ –Њ –љ–µ—А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –њ–ї–∞–љ–µ—В—Л.
. –Ю—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В —Н—В–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞, –Ї–Њ—В–Њ—А–Њ–µ —З–∞—Б—В–Њ –Љ–Њ–ґ–љ–Њ –љ–∞–±–ї—О–і–∞—В—М –љ–∞ –њ—А–∞–Ї—В–Є–Ї–µ, –≥–Њ–≤–Њ—А–Є—В –њ—А–µ–ґ–і–µ –≤—Б–µ–≥–Њ –Њ –љ–µ—А–∞–≤–љ–Њ–≤–µ—Б–љ–Њ–Љ —Б–Њ—Б—В–Њ—П–љ–Є–Є –њ–ї–∞–љ–µ—В—Л.
–Ы–µ–Ї—Ж–Є—П 7
–§–Њ—А–Љ—Г–ї–∞ –°–Њ–Љ–Є–ї—М—П–љ—Л. –Э–Њ—А–Љ–∞–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є. –Т—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Ы–Њ–Ї–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П. –Ъ—А–Є–≤–Є–Ј–љ—Л –Є —А–∞–і–Є—Г—Б—Л –Ї—А–Є–≤–Є–Ј–љ—Л –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П –Т—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Я–µ—А–≤—Л–µ –Є –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤ –Њ–Ї–Њ–ї–Њ–Ј–µ–Љ–љ–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ.
–Э–Њ—А–Љ–∞–ї—М–љ–Њ–µ –њ–Њ–ї–µ —В—П–ґ–µ—Б—В–Є –Ч–µ–Љ–ї–Є
–§–Њ—А–Љ—Г–ї–∞ –°–Њ–Љ–Є–ї—М—П–љ—Л
–Ш—В–∞–ї—М—П–љ—Б–Ї–Є–є –≥–µ–Њ–і–µ–Ј–Є—Б—В –°–Њ–Љ–Є–ї—М—П–љ–∞ (Somigliana)–≤ 1929 –≥–Њ–і—Г –њ–Њ–ї—Г—З–Є–ї —В–Њ—З–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г, –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—Й—Г—О —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П. –Т–Њ–њ—А–µ–Ї–Є –њ—А–∞–≤–Є–ї–∞–Љ —А—Г—Б—Б–Ї–Њ–≥–Њ —П–Ј—Л–Ї–∞ —Н—В–∞ —Д–Њ—А–Љ—Г–їa –≤–Њ—И–ї–∞ –≤ —А—Г—Б—Б–Ї—Г—О –ї–Є—В–µ—А–∞—В—Г—А—Г –Ї–∞–Ї —Д–Њ—А–Љ—Г–ї–∞ –°–Њ–Љ–Є–ї—М—П–љ–∞, –Ї–∞–Ї –µ—Б–ї–Є –±—Л –µ–≥–Њ —Д–∞–Љ–Є–ї–Є—П –±—Л–ї–∞ –°–Њ–Љ–Є–ї—М—П–љ. –Ь—Л –±—Г–і–µ–Љ —Б–Ї–ї–Њ–љ—П—В—М –µ–≥–Њ —Д–∞–Љ–Є–ї–Є—О, –њ–Њ—Н—В–Њ–Љ—Г –і–Њ–ї–ґ–љ—Л –љ–∞–Ј–≤–∞—В—М –µ–≥–Њ —Д–Њ—А–Љ—Г–ї—Г –Є–Љ–µ–љ–µ–Љ –°–Њ–Љ–Є–ї—М—П–љ—Л.
–Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є, –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е
u,v,w –Є–Љ–µ–µ—В –≤–Є–і (—Д–Њ—А–Љ—Г–ї–∞ 6. 19):
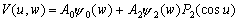
–Я–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –Њ—В–ї–Є—З–∞–µ—В—Б—П —В–µ–Љ, —З—В–Њ –∞–і–і–Є—В–Є–≤–љ–Њ –≤–Ї–ї—О—З–∞–µ—В –≤ —Б–µ–±—П —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї
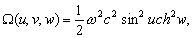
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
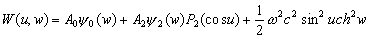 (7.1)
(7.1)
–£—З–Є—В—Л–≤–∞—П, —З—В–Њ
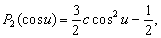 –њ–Њ–ї—Г—З–Є–Љ
–њ–Њ–ї—Г—З–Є–Љ
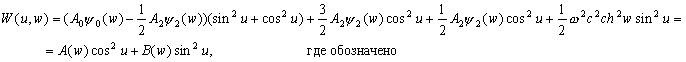

–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞
 , –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ—А–Њ–і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞—В—М —Д—Г–љ–Ї—Ж–Є—О
, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –њ—А–Њ–і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞—В—М —Д—Г–љ–Ї—Ж–Є—О  –≤–і–Њ–ї—М –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–є –ї–Є–љ–Є–Є
–≤–і–Њ–ї—М –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ–є –ї–Є–љ–Є–Є 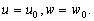 –≠–ї–µ–Љ–µ–љ—В –і—Г–≥–Є –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —А–∞–≤–µ–љ
–≠–ї–µ–Љ–µ–љ—В –і—Г–≥–Є –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —А–∞–≤–µ–љ  –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Ы–∞–Љ–µ, –Ї–Њ—В–Њ—А—Л–є, –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —А–∞–≤–µ–љ
–Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Ы–∞–Љ–µ, –Ї–Њ—В–Њ—А—Л–є, –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ, —А–∞–≤–µ–љ
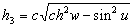
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є –њ–Њ –љ–Њ—А–Љ–∞–ї–Є –Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞
 –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
–Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
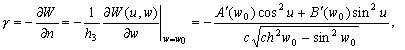
–≥–і–µ
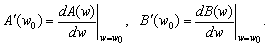
–Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
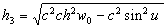 ,
,
–љ–Њ
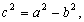
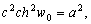
–њ–Њ—Н—В–Њ–Љ—Г
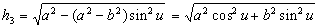
–Ґ–µ–њ–µ—А—М —Г–і–µ–ї—М–љ—Г—О —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
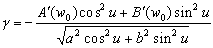 (7.2)
(7.2)
–Ь—Л –њ–Њ–ї—Г—З–Є–ї–Є –Є—Б–Ї–Њ–Љ—Г—О —Д–Њ—А–Љ—Г–ї—Г –і–ї—П —Г–і–µ–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞. –Ю–і–љ–∞–Ї–Њ –љ–∞–Љ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є–Ј–±–∞–≤–Є—В—М—Б—П –Њ—В –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е
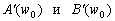 . –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ —В–Њ—З–Ї–∞ u=0,
. –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ —В–Њ—З–Ї–∞ u=0,  —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –њ–Њ–ї—О—Б—Г —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –∞ —В–Њ—З–Ї–∞
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –њ–Њ–ї—О—Б—Г —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –∞ —В–Њ—З–Ї–∞ 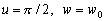 - —Н–Ї–≤–∞—В–Њ—А—Г. –С—Г–і–µ–Љ —Б–љ–∞–±–ґ–∞—В—М –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ –і–ї—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є–љ–і–µ–Ї—Б–∞–Љ–Є p –Є –µ. –Ш–Ј (7.2) –њ–Њ–ї—Г—З–Є–Љ
- —Н–Ї–≤–∞—В–Њ—А—Г. –С—Г–і–µ–Љ —Б–љ–∞–±–ґ–∞—В—М –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ –і–ї—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є–љ–і–µ–Ї—Б–∞–Љ–Є p –Є –µ. –Ш–Ј (7.2) –њ–Њ–ї—Г—З–Є–Љ
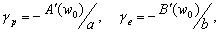
—В–Њ –µ—Б—В—М  .
.
–Ґ–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Г (7.2) –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
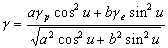 (7.3)
(7.3)
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М —Д–Њ—А–Љ—Г–ї—Г –°–Њ–Љ–Є–ї—М—П–љ—Л –≤ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ–Љ –≤–Є–і–µ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ—В —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В –њ–µ—А–µ–є—В–Є –Ї –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є. –°–Њ–њ–Њ—Б—В–∞–≤–Є–Љ –і–≤–µ —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В –і–ї—П —В–Њ—З–µ–Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞

–≥–і–µ
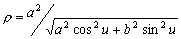 (—Б–Љ. –ї–µ–Ї—Ж–Є—О 2)
(—Б–Љ. –ї–µ–Ї—Ж–Є—О 2)
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
v=L ( –њ–Њ–љ—П—В–Є—П –і–Њ–ї–≥–Њ—В—Л –≤ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є –Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞–ї—М–љ–Њ–є —Б–Є—Б—В–µ–Љ–∞—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ–≤–њ–∞–і–∞—О—В), –њ–Њ—Н—В–Њ–Љ—Г
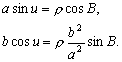
–Ю—В—Б—О–і–∞
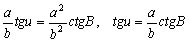
–Ш–Љ–µ–µ–Љ –Њ—З–µ–≤–Є–і–љ—Л–µ –≤—Л—А–∞–ґ–µ–љ–Є—П –і–ї—П —Б–≤—П–Ј–Є
u –Є B:

–Я–Њ—Б–ї–µ –љ–µ—Б–ї–Њ–ґ–љ—Л—Е —Г–њ—А–Њ—Й–µ–љ–Є–є, –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ –њ–Њ–ї—Г—З–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –°–Њ–Љ–Є–ї—М—П–љ—Л
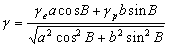 (7.4)
(7.4)
–Э–Њ—А–Љ–∞–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є
–Т –≥–µ–Њ–і–µ–Ј–Є–Є –Є –≥–µ–Њ—Д–Є–Ј–Є–Ї–µ –Њ—Б–љ–Њ–≤–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Њ–є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П —П–≤–ї—П—О—В—Б—П –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є, –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –Ї–∞–Ї —А–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –љ–∞–±–ї—О–івХ¶–љ–љ—Л–Љ –Ј–љ–∞—З–µ–љ–Є–µ–Љ —Г–і–µ–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є –њ—А–µ–і–≤—Л—З–Є—Б–ї–µ–љ–љ—Л–Љ. –Ю–і–љ–∞–Ї–Њ —Б—А–∞–≤–љ–Є–≤–∞—В—М —Н—В–Є –Ј–љ–∞—З–µ–љ–Є—П –Љ–Њ–ґ–љ–Њ —В–Њ–ї—М–Ї–Њ, –≤ —Б–ї—Г—З–∞–µ –Ї–Њ–≥–і–∞ –љ–∞–±–ї—О–івХ¶–љ–љ–Њ–µ –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є—П –Њ—В–љ–Њ—Б—П—В—Б—П –Ї –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ —В–Њ—З–Ї–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞. –Т –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В–Є –ґ–µ –љ–Њ—А–Љ–∞–ї—М–љ—Г—О —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є –Њ—В–љ–Њ—Б—П—В –Ї –Њ–±—Й–µ–Љ—Г –Ј–µ–Љ–љ–Њ–Љ—Г —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г, –∞ –љ–∞–±–ї—О–і–µ–љ–љ–Њ–µ вИЪ –Ї —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є. –Ґ–∞–Ї–Є–µ –∞–љ–Њ–Љ–∞–ї–Є–Є –≤ –≥–µ–Њ–і–µ–Ј–Є–Є –Є–Љ–µ–љ—Г—О—В —Б–Љ–µ—И–∞–љ–љ—Л–Љ–Є –∞–љ–Њ–Љ–∞–ї–Є—П–Љ–Є. –Ш–љ–Њ–≥–і–∞ –љ–∞–±–ї—О–івХ¶–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —А–µ–і—Г—Ж–Є—А—Г—О—В, —В–Њ –µ—Б—В—М –≤–љ–Њ—Б—П—В –њ–Њ–њ—А–∞–≤–Ї–Є, –њ–Њ–Ј–≤–Њ–ї—П—О—Й–Є–µ –≤—Л—З–Є—Б–ї–Є—В—М –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –≤ –і—А—Г–≥–Њ–є —В–Њ—З–Ї–µ –Є–ї–Є –љ–∞ –і—А—Г–≥–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Я—А–Є —Н—В–Њ–Љ –Є—Б–њ–Њ–ї—М–Ј—Г—О—В —В—Г –Є–ї–Є –Є–љ—Г—О –≥–Є–њ–Њ—В–µ–Ј—Г –Њ —Б—В—А–Њ–µ–љ–Є–Є –≤–µ—А—Е–љ–Є—Е —Б–ї–ЊвХ¶–≤ –Ч–µ–Љ–ї–Є. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –њ–Њ–љ—П—В–Є–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є —Г—В–Њ—З–љ—П—О—В, –љ–∞–њ—А–Є–Љ–µ—А
–≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є –≤ —А–µ–і—Г–Ї—Ж–Є–Є –§–∞—П –Є–ї–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є –≤ —А–µ–і—Г–Ї—Ж–Є–Є –У–ї–µ–љ–љ–Є.
–Ш—В–∞–Ї, –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Њ—В–љ–Њ—Б—П—В –Ї –Њ–±—Й–µ–Љ—Г –Ј–µ–Љ–љ–Њ–Љ—Г —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г, –Ї–Њ—В–Њ—А–Њ–µ –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ —Б—В—А–Њ–≥–Њ–є —Д–Њ—А–Љ—Г–ї–µ (7.4). –≠—В–∞ —Д–Њ—А–Љ—Г–ї–∞ —Б—В—А–Њ–≥–∞—П –ї–Є—И—М –≤ —В–Њ–Љ —Б–ї—Г—З–∞–µ, –Ї–Њ–≥–і–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –µ—Б—В—М –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П, —З–µ–≥–Њ –≤ –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В–Є –љ–µ—В. –Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ –≤ –Ј–∞–і–∞—З–∞—Е –≥–µ–Њ–і–µ–Ј–Є–Є –Є –≥–µ–Њ—Д–Є–Ј–Є–Ї–Є –њ—А–Є–Љ–µ–љ—П—О—В –њ—А–Є–±–ї–Є–ґ–µ–љ–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Я—А–Є—ЗвХ¶–Љ —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤, –≤—Е–Њ–і—П—Й–Є–µ –≤ —Н—В—Г —Д–Њ—А–Љ—Г–ї—Г, —Г—В–≤–µ—А–ґ–і–∞—О—В –љ–∞ –У–µ–љ–µ—А–∞–ї—М–љ–Њ–є –∞—Б—Б–∞–Љ–±–ї–µ–µ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ–Њ–≥–Њ –°–Њ—О–Ј–∞ –≥–µ–Њ–і–µ–Ј–Є–Є –Є –≥–µ–Њ—Д–Є–Ј–Є–Ї–Є.
–Т–µ—А–љвХ¶–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–µ –°–Њ–Љ–Є–ї—М—П–љ—Л. –£–њ—А–Њ—Б—В–Є–Љ –µвХ¶, –Њ—В–±—А–∞—Б—Л–≤–∞—П –Љ–∞–ї—Л–µ –≤–µ–ї–Є—З–Є–љ—Л –њ–Њ—А—П–і–Ї–∞ –Ї—Г–±–∞ —Б–ґ–∞—В–Є—П. –Т–≤–µ–івХ¶–Љ –≤ –Њ–±—А–∞—Й–µ–љ–Є–µ –њ–Њ–љ—П—В–Є—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–ґ–∞—В–Є—П  –Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П
–Є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ —Б–ґ–∞—В–Є—П 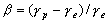 . –Ю–±–µ –≤–µ–ї–Є—З–Є–љ—Л –Љ—Л –±—Г–і–µ–Љ —Б—З–Є—В–∞—В—М –Њ–і–љ–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Љ–∞–ї–Њ—Б—В–Є. –Т —Д–Њ—А–Љ—Г–ї–µ –°–Њ–Љ–Є–ї—М—П–љ—Л –Љ—Л –і–Њ–ї–ґ–љ—Л –Ј–∞–Љ–µ–љ–Є—В—М b –≤–µ–ї–Є—З–Є–љ–Њ–є b=a(1-a
), –∞ –≤–Љ–µ—Б—В–Њ
. –Ю–±–µ –≤–µ–ї–Є—З–Є–љ—Л –Љ—Л –±—Г–і–µ–Љ —Б—З–Є—В–∞—В—М –Њ–і–љ–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Љ–∞–ї–Њ—Б—В–Є. –Т —Д–Њ—А–Љ—Г–ї–µ –°–Њ–Љ–Є–ї—М—П–љ—Л –Љ—Л –і–Њ–ї–ґ–љ—Л –Ј–∞–Љ–µ–љ–Є—В—М b –≤–µ–ї–Є—З–Є–љ–Њ–є b=a(1-a
), –∞ –≤–Љ–µ—Б—В–Њ 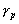 –≤–Ј—П—В—М
–≤–Ј—П—В—М  :
:
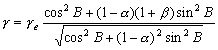
–†–∞–Ј–ї–∞–≥–∞—П –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ —Б—В–µ–њ–µ–љ–љ–Њ–є —А—П–і –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ a
–Є b
, –±—Г–і–µ–Љ –Є–Љ–µ—В—М
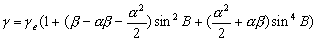
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
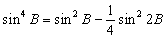 , –њ–Њ–ї—Г—З–µ–љ–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
, –њ–Њ–ї—Г—З–µ–љ–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і

–Ш—В–∞–Ї, —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –≤—А–∞—Й–µ–љ–Є—П (—Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ) —Б —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ –Љ–∞–ї—Л—Е –≤—В–Њ—А–Њ–є —Б—В–µ–њ–µ–љ–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Б–ґ–∞—В–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–∞ —Д–Њ—А–Љ—Г–ї–Њ–є
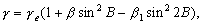
–≥–і–µ 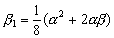 . (7.5)
. (7.5)
—З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤
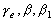 –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є. –Э–∞ –У–µ–љ–µ—А–∞–ї—М–љ–Њ–є –Р—Б—Б–∞–Љ–±–ї–µ–µ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ–Њ–≥–Њ –°–Њ—О–Ј–∞, —Б–Њ—Б—В–Њ—П–≤—И–µ–є—Б—П –≤ –Ь–Њ—Б–Ї–≤–µ –≤ 1971 –≥–Њ–і—Г —А–µ–Ї–Њ–Љ–µ–љ–і–Њ–≤–∞–љ—Л —Б–ї–µ–і—Г—О—Й–Є–µ –Ј–љ–∞—З–µ–љ–Є—П (—Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є вИЪ –≤ –Љ–Є–ї–ї–Є–≥–∞–ї–∞—Е)
–Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є. –Э–∞ –У–µ–љ–µ—А–∞–ї—М–љ–Њ–є –Р—Б—Б–∞–Љ–±–ї–µ–µ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ–Њ–≥–Њ –°–Њ—О–Ј–∞, —Б–Њ—Б—В–Њ—П–≤—И–µ–є—Б—П –≤ –Ь–Њ—Б–Ї–≤–µ –≤ 1971 –≥–Њ–і—Г —А–µ–Ї–Њ–Љ–µ–љ–і–Њ–≤–∞–љ—Л —Б–ї–µ–і—Г—О—Й–Є–µ –Ј–љ–∞—З–µ–љ–Є—П (—Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є вИЪ –≤ –Љ–Є–ї–ї–Є–≥–∞–ї–∞—Е)
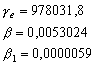
–Т—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
–У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї, –∞ –≤–µ—А–љ–µ–µ —Б–Є–ї–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –і–ї—П —Г–і–µ–ї—М–љ–Њ–є —Б–Є–ї—Л
—В—П–ґ–µ—Б—В–Є —П–≤–ї—П–µ—В—Б—П –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є, –њ—А–Є–љ–Є–Љ–∞—О—Й–µ–є –µ–і–Є–љ—Б—В–≤–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤ –Ї–∞–ґ–і–Њ–є —В–Њ—З–Ї–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞. –Я–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ (—Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є) –Ї–∞–Ї —Г–≥–Њ–і–љ–Њ –њ–ї–Њ—В–љ–Њ –Ј–∞–њ–Њ–ї–љ—П—О—В –≤–љ–µ—И–љ–µ–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –љ–Є–≥–і–µ –љ–µ –њ–µ—А–µ—Б–µ–Ї–∞—П—Б—М. –Т–µ–Ї—В–Њ—А —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –≤ —В–Њ—З–Ї–µ –† –љ–∞–њ—А–∞–≤–ї–µ–љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –Ї —Н–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —Н—В—Г —В–Њ—З–Ї—Г. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤–Њ –≤–љ–µ—И–љ–µ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Њ–±—А–∞–Ј—Г–µ—В —Б–Є–ї–Њ–≤–Њ–µ –њ–Њ–ї–µ. –Ю–љ–Њ –њ—А–Њ–љ–Є–Ј–∞–љ–Њ —Б–Є–ї–Њ–≤—Л–Љ–Є –ї–Є–љ–Є—П–Љ–Є, –њ—А–Є—З–µ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Ї —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є.
–Ш–Ј —Б–Ї–∞–Ј–∞–љ–љ–Њ–≥–Њ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —Б–Є–ї–Њ–≤—Л–µ –ї–Є–љ–Є–Є –љ–µ –Љ–Њ–≥—Г—В –њ–µ—А–µ—Б–µ–Ї–∞—В—М—Б—П, —В–∞–Ї –Ї–∞–Ї –≤ —В–Њ—З–Ї–µ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –љ–µ –Љ–Њ–ґ–µ—В —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞—В—М –і–≤–∞ –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Т–µ–Ї—В–Њ—А —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є (—Г–і–µ–ї—М–љ–Њ–є) –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
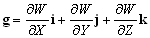 ,
,
–≥–і–µ
i,j,k - –Њ—А—В—Л, –љ–∞–њ—А–∞–≤–ї–µ–љ–љ—Л–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –≤–і–Њ–ї—М –Њ—Б–µ–є PX, PY –Є PZ. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є–µ –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є —Б—Г—В—М –њ–µ—А–≤—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є
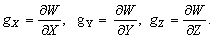
–Т –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є –Є –≥–µ–Њ—Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ—А–∞–Ї—В–Є–Ї–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—О—В —В–∞–Ї–ґ–µ –Є –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –Ї–Њ—В–Њ—А—Л–µ –Њ—В–Љ–µ—З–∞—О—В –і–≤–Њ–є–љ—Л–Љ–Є –љ–Є–ґ–љ–Є–Љ–Є –Є–љ–і–µ–Ї—Б–∞–Љ–Є
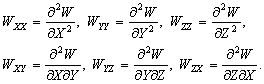
–Т—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Љ–Њ–ґ–љ–Њ –Є–Ј–Њ–±—А–∞–Ј–Є—В—М –≤ –≤–Є–і–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–є –Љ–∞—В—А–Є—Ж—Л
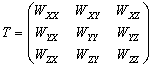 . –Я–Њ–ї—Г—З–µ–љ–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Љ–µ–µ—В 9 —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –љ–Њ –љ–µ –≤—Б–µ –Њ–љ–Є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
. –Я–Њ–ї—Г—З–µ–љ–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Љ–µ–µ—В 9 —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –љ–Њ –љ–µ –≤—Б–µ –Њ–љ–Є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ 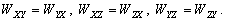 –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Б–ї–µ–і —Н—В–Њ–є –Љ–∞—В—А–Є—Ж—Л –µ—Б—В—М –ї–∞–њ–ї–∞—Б–Є–∞–љ, –њ–Њ—Н—В–Њ–Љ—Г
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, —Б–ї–µ–і —Н—В–Њ–є –Љ–∞—В—А–Є—Ж—Л –µ—Б—В—М –ї–∞–њ–ї–∞—Б–Є–∞–љ, –њ–Њ—Н—В–Њ–Љ—Г
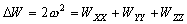 (7.6)
(7.6)
–Ю—Б—В–∞вХ¶—В—Б—П 5 –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —Н—В–Њ–є –Љ–∞—В—А–Є—Ж—Л, –Ї–Њ—В–Њ—А–∞—П –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є —В–µ–љ–Ј–Њ—А –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
.
–†–∞—Б—Б—Г–ґ–і–µ–љ–Є—П –Љ–Њ–ґ–љ–Њ –њ—А–Њ–і–Њ–ї–ґ–Є—В—М –Є –і–∞–ї—М—И–µ, –Њ–±—А–∞–Ј—Г—П —В—А–µ—В—М–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ, —З–µ—В–≤вХ¶—А—В—Л–µ –Є —В.–і. –Э–Њ —Г–ґ–µ —В—А–µ—В—М–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –љ–µ–ї—М–Ј—П –Є–Ј–Њ–±—А–∞–Ј–Є—В—М –≤ –≤–Є–і–µ –Љ–∞—В—А–Є—Ж—Л: —Н—В–Њ –±—Г–і–µ—В –Ї—Г–± —А–∞–Ј–Љ–µ—А–Њ–Љ 3—Е3, –Ї–Њ—В–Њ—А—Л–є –љ–∞ –і–≤—Г—Е–Љ–µ—А–љ–Њ–Љ –ї–Є—Б—В–µ –±—Г–Љ–∞–≥–Є –Є–Ј–Њ–±—А–∞–Ј–Є—В—М —В—А—Г–і–љ–Њ. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –Є–Ј–Њ–±—А–∞–Ј–Є—В—М –≤ –≤–Є–і–µ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е —Д–Є–≥—Г—А –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –±–Њ–ї–µ–µ –≤—Л—Б–Њ–Ї–Є—Е –њ–Њ—А—П–і–Ї–Њ–≤. –≠—В–Њ –±—Г–і—Г—В —В–µ–љ–Ј–Њ—А—Л –≤—Л—Б–Њ–Ї–Є—Е –≤–∞–ї–µ–љ—В–љ–Њ—Б—В–µ–є.
–≠–Ї–≤–Є–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Г—О –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –≤ –Њ–Ї—А–µ—Б—В–љ–Њ—Б—В–Є —В–Њ—З–Ї–Є
 –Љ–Њ–ґ–љ–Њ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞—В—М –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О вИЪ —Н—В–Њ –±—Г–і–µ—В –Ї–∞—Б–∞—В–µ–ї—М–љ–∞—П –њ–ї–Њ—Б–Ї–Њ—Б—В—М- —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ, –≥–Є–њ–µ—А–±–Њ–ї–Њ–Є–і–Њ–Љ –Є –і—А. –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—П–Љ–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Т –њ–Њ—Б–ї–µ–і–љ–µ–Љ —Б–ї—Г—З–∞–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
–Љ–Њ–ґ–љ–Њ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞—В—М –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О вИЪ —Н—В–Њ –±—Г–і–µ—В –Ї–∞—Б–∞—В–µ–ї—М–љ–∞—П –њ–ї–Њ—Б–Ї–Њ—Б—В—М- —Н–ї–ї–Є–њ—Б–Њ–Є–і–Њ–Љ, –≥–Є–њ–µ—А–±–Њ–ї–Њ–Є–і–Њ–Љ –Є –і—А. –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—П–Љ–Є –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Т –њ–Њ—Б–ї–µ–і–љ–µ–Љ —Б–ї—Г—З–∞–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
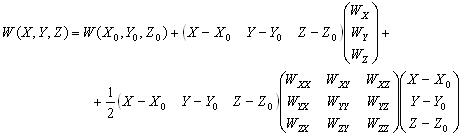 (7.7)
(7.7)
–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –њ–Њ–ї—Г—З–Є–Љ, –Њ—В–±—А–∞—Б—Л–≤–∞—П –≤ (7.7) –Ї–≤–∞–і—А–∞—В–Є—З–љ—Г—О —Д–Њ—А–Љ—Г
 (7.8)
(7.8)
–≥–і–µ
 . –Т–µ–ї–Є—З–Є–љ—Л
. –Т–µ–ї–Є—З–Є–љ—Л —Б—Г—В—М –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Ш–Ј–Љ–µ–љ—П—П –њ–Њ—Б—В–Њ—П–љ–љ—Г—О
—Б—Г—В—М –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Ш–Ј–Љ–µ–љ—П—П –њ–Њ—Б—В–Њ—П–љ–љ—Г—О 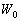 , –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–µ–є, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е —В–Њ–є, —З—В–Њ –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –†.
, –њ–Њ–ї—Г—З–Є–Љ —Б–µ–Љ–µ–є—Б—В–≤–Њ –њ–ї–Њ—Б–Ї–Њ—Б—В–µ–є, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е —В–Њ–є, —З—В–Њ –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –†.
–Ф–ї—П —Г–њ—А–Њ—Й–µ–љ–Є—П –≤—Л–Ї–ї–∞–і–Њ–Ї, —З–∞—Б—В–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –Љ–µ—Б—В–љ–Њ–є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –≤—Л–±–Є—А–∞—О—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: –Њ—Б—М
PX –љ–∞–њ—А–∞–≤–ї—П—О—В –љ–∞ —Б–µ–≤–µ—А, –Њ—Б—М PY вИЪ —Б—В—А–Њ–≥–Њ –љ–∞ –≤–Њ—Б—В–Њ–Ї, –∞ –Њ—Б—М PZ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –≤–µ–Ї—В–Њ—А–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ –≤–љ–Є–Ј. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ  . –£—А–∞–≤–љ–µ–љ–Є–µ(7.8) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
. –£—А–∞–≤–љ–µ–љ–Є–µ(7.8) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і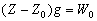 . –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –њ—А–Є—А–∞—Й–µ–љ–Є–µ –≤—Л—Б–Њ—В—Л –±—Г–Ї–≤–Њ–є h, –њ–Њ–ї—Г—З–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –њ—А–Є—А–∞—Й–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
. –Ю–±–Њ–Ј–љ–∞—З–Є–Љ –њ—А–Є—А–∞—Й–µ–љ–Є–µ –≤—Л—Б–Њ—В—Л –±—Г–Ї–≤–Њ–є h, –њ–Њ–ї—Г—З–Є–Љ —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –њ—А–Є—А–∞—Й–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ 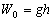 , –Ї–Њ—В–Њ—А—Г—О —З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д–Њ—А–Љ—Г–ї–Њ–є –С—А—Г–љ—Б–∞.
, –Ї–Њ—В–Њ—А—Г—О —З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д–Њ—А–Љ—Г–ї–Њ–є –С—А—Г–љ—Б–∞.
–Ю–њ—А–µ–і–µ–ї–Є–Љ –Ї—А–Є–≤–Є–Ј–љ—Г –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є
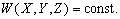 –†–µ—И–Є–Љ —Н—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є Z: Z=Z(X,Y) –Ґ–Њ–≥–і–∞ —А–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л R –≤ —В–Њ—З–Ї–µ –† –њ–Њ —Д–Њ—А–Љ—Г–ї–µ –Ь–Њ–љ–ґ–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є
–†–µ—И–Є–Љ —Н—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є Z: Z=Z(X,Y) –Ґ–Њ–≥–і–∞ —А–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л R –≤ —В–Њ—З–Ї–µ –† –њ–Њ —Д–Њ—А–Љ—Г–ї–µ –Ь–Њ–љ–ґ–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є , –≥–і–µ –Р вИЪ —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –Њ–±—А–∞–Ј—Г–µ—В –Њ—Б—М PX —Б –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П. –Т –і–∞–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–µ –±—Г–Ї–≤–∞–Љ–Є r,s,t –Њ–±–Њ–Ј–љ–∞—З–µ–љ—Л –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ
, –≥–і–µ –Р вИЪ —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –Њ–±—А–∞–Ј—Г–µ—В –Њ—Б—М PX —Б –њ–ї–Њ—Б–Ї–Њ—Б—В—М—О –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П. –Т –і–∞–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–µ –±—Г–Ї–≤–∞–Љ–Є r,s,t –Њ–±–Њ–Ј–љ–∞—З–µ–љ—Л –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ
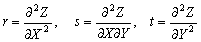
–Э–∞—И–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —Г—А–Њ–≤–љ—П –Ј–∞–і–∞–љ–∞ –љ–µ —А–∞–Ј—А–µ—ИвХ¶–љ–љ–Њ–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л. –Я–Њ—Н—В–Њ–Љ—Г –љ–∞–Љ –љ—Г–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –Ї—А–Є–≤–Є–Ј–љ—Л —Б–µ—З–µ–љ–Є—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –Ј–∞–і–∞–љ–љ–Њ–є –≤ –љ–µ—П–≤–љ–Њ–Љ –≤–Є–і–µ. –Я—А–Њ–і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М
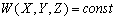 –њ–Њ –Њ–і–љ–Њ–є –Є–Ј –Ї–Њ–Њ—А–і–Є–љ–∞—В, –љ–∞–њ—А–Є–Љ–µ—А –њ–Њ X. –Ґ–Њ–≥–і–∞
–њ–Њ –Њ–і–љ–Њ–є –Є–Ј –Ї–Њ–Њ—А–і–Є–љ–∞—В, –љ–∞–њ—А–Є–Љ–µ—А –њ–Њ X. –Ґ–Њ–≥–і–∞
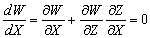
–Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г—П –≤—В–Њ—А–Њ–є —А–∞–Ј, –њ–Њ–ї—Г—З–Є–Љ,
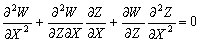
–Э–Њ —В–Њ—З–Ї–∞ –† –µ—Б—В—М —В–Њ—З–Ї–∞ –Ї–∞—Б–∞–љ–Є—П, –≥–і–µ
 , –њ–Њ—Н—В–Њ–Љ—Г
, –њ–Њ—Н—В–Њ–Љ—Г  . –Ш—Б–њ–Њ–ї—М–Ј—Г—П –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –Ь–Њ–љ–ґ–∞, –±—Г–і–µ–Љ –Є–Љ–µ—В—М
. –Ш—Б–њ–Њ–ї—М–Ј—Г—П –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П –Ь–Њ–љ–ґ–∞, –±—Г–і–µ–Љ –Є–Љ–µ—В—М 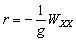 . –†–∞—Б—Б—Г–ґ–і–∞—П –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ, –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–Є–Љ
. –†–∞—Б—Б—Г–ґ–і–∞—П –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ, –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–Є–Љ 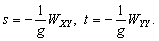
–Ґ–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї–∞ –Ь–Њ–љ–ґ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
 (7.9)
(7.9)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –≤–∞–ґ–љ—Л–µ —З–∞—Б—В–љ—Л–µ —Б–ї—Г—З–∞–Є
:
–Љ–µ—А–Є–і–Є–Њ–љ–∞–ї—М–љ–Њ–µ —Б–µ—З–µ–љ–Є–µ (–Р=0) –†–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л: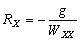 . –Ъ—А–Є–≤–Є–Ј–љ–∞:
. –Ъ—А–Є–≤–Є–Ј–љ–∞: 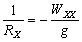 (7.10)
—Б–µ—З–µ–љ–Є–µ –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї–µ (–Р=90°
). –†–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л:
(7.10)
—Б–µ—З–µ–љ–Є–µ –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї–µ (–Р=90°
). –†–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л: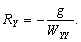 –Ъ—А–Є–≤–Є–Ј–љ–∞:
–Ъ—А–Є–≤–Є–Ј–љ–∞: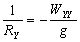 (7.11)
(7.11)
–Ш—В–∞–Ї, –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є
 –Њ–њ—А–µ–і–µ–ї—П—О—В –Ї—А–Є–≤–Є–Ј–љ—Г (—А–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л) –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ю—Б—В–∞вХ¶—В—Б—П –≤—Л—П—Б–љ–Є—В—М —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є –Є–ї–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –µ—ЙвХ¶ —В—АвХ¶—Е –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е:
–Њ–њ—А–µ–і–µ–ї—П—О—В –Ї—А–Є–≤–Є–Ј–љ—Г (—А–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л) –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ю—Б—В–∞вХ¶—В—Б—П –≤—Л—П—Б–љ–Є—В—М —Д–Є–Ј–Є—З–µ—Б–Ї–Є–є –Є–ї–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –µ—ЙвХ¶ —В—АвХ¶—Е –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е:  .
.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
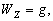 —В–Њ
—В–Њ 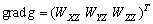 –У–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Г—О –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Г —Н—В–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ –љ–∞–Ј—Л–≤–∞—О—В –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–Љ –≥—А–∞–і–Є–µ–љ—В–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –∞ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Г—О –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Г вИЪ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–Љ –≥—А–∞–і–Є–µ–љ—В–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є.
–У–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Г—О –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Г —Н—В–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ –љ–∞–Ј—Л–≤–∞—О—В –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–Љ –≥—А–∞–і–Є–µ–љ—В–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –∞ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Г—О –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Г вИЪ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–Љ –≥—А–∞–і–Є–µ–љ—В–Њ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є.
–Т—Л–≤–µ–і–µ–Љ —В–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Х—Б–ї–Є —В–Њ—З–Ї–∞ –† –≤–љ–µ—И–љ—П—П, —В–Њ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ
 . –Ф–ї—П –≤–љ—Г—В—А–µ–љ–љ–µ–є —В–Њ—З–Ї–Є —Г—А–∞–≤–љ–µ–љ–Є–µ –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –њ—А–µ–≤—А–∞—Й–∞–µ—В—Б—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Я—Г–∞—Б—Б–Њ–љ–∞, —В–Њ–≥–і–∞
. –Ф–ї—П –≤–љ—Г—В—А–µ–љ–љ–µ–є —В–Њ—З–Ї–Є —Г—А–∞–≤–љ–µ–љ–Є–µ –Ы–∞–њ–ї–∞—Б–∞ –і–ї—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –њ—А–µ–≤—А–∞—Й–∞–µ—В—Б—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Я—Г–∞—Б—Б–Њ–љ–∞, —В–Њ–≥–і–∞ 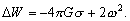 –Я–µ—А–µ–њ–Є—И–µ–Љ —А–∞–≤–µ–љ—Б—В–≤–Њ –≤ –љ–∞—И–Є—Е –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П—Е
–Я–µ—А–µ–њ–Є—И–µ–Љ —А–∞–≤–µ–љ—Б—В–≤–Њ –≤ –љ–∞—И–Є—Е –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П—Е
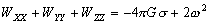
–Ш–Ј —Д–Њ—А–Љ—Г–ї (7.10) –Є (7.11) —Б–ї–µ–і—Г–µ—В, —З—В–Њ
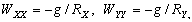 –њ–Њ—Н—В–Њ–Љ—Г
–њ–Њ—Н—В–Њ–Љ—Г
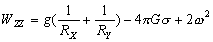 (7.12)
(7.12)
–Ь—Л –≤–Є–і–Є–Љ, —З—В–Њ –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М —А–∞–і–Є—Г—Б—Л –Ї—А–Є–≤–Є–Ј–љ—Л –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Б–µ—З–µ–љ–Є–є —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –њ–ї–Њ—В–љ–Њ—Б—В—М –Є —Г–≥–ї–Њ–≤—Г—О —Б–Ї–Њ—А–Њ—Б—В—М –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є. –Э–∞–Њ–±–Њ—А–Њ—В, –µ—Б–ї–Є –љ–∞—Б –Є–љ—В–µ—А–µ—Б—Г–µ—В –њ–ї–Њ—В–љ–Њ—Б—В—М –њ–Њ—А–Њ–і, –Њ–Ї—А—Г–ґ–∞—О—Й–Є—Е —В–Њ—З–Ї—Г –љ–∞–±–ї—О–і–µ–љ–Є—П, –љ—Г–ґ–љ–Њ –Є–Ј–Љ–µ—А–Є—В—М –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–є –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Я–Њ—Н—В–Њ–Љ—Г –Є–Ј–Љ–µ—А–µ–љ–Є–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —П–≤–ї—П–µ—В—Б—П –Њ—З–µ–љ—М –≤–∞–ґ–љ–Њ–є –Ј–∞–і–∞—З–µ–є –і–ї—П —Ж–µ–ї–µ–є –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–є —А–∞–Ј–≤–µ–і–Ї–Є
.
–Т –Ј–∞–Ї–ї—О—З–µ–љ–Є–Є, –њ—А–Є–≤–µ–івХ¶–Љ –Њ—Б–љ–Њ–≤–љ—Л–µ —Д–Њ—А–Љ—Г–ї—Л –і–ї—П –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –Ъ–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є, –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —Г—А–Њ–≤–љ—П –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —П–≤–ї—П–µ—В—Б—П —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П.
–†–∞–і–Є—Г—Б –Ї—А–Є–≤–Є–Ј–љ—Л –Љ–µ—А–Є–і–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —А–∞–≤–µ–љ
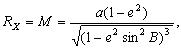
–∞ —Б–µ—З–µ–љ–Є—П –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї–µ
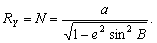 (7.13)
(7.13)
–Ю–≥—А–∞–љ–Є—З–Є–≤–∞—П—Б—М –Љ–∞–ї—Л–Љ–Є –њ–Њ—А—П–і–Ї–∞ —Б–ґ–∞—В–Є—П, –њ–Њ–ї—Г—З–Є–Љ
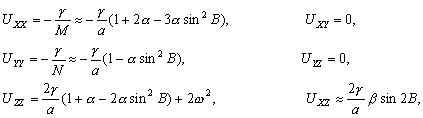 (7.14)
(7.14)
–≥–і–µ b
–љ—Г–ґ–љ–Њ –≤–Ј—П—В—М –Є–Ј –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Д–Њ—А–Љ—Г–ї—Л (7.5).
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
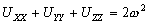 - –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –Љ–∞–ї–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю—Б–љ–Њ–≤–љ–Њ–є –≤–Ї–ї–∞–і –≤ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–є –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –≤–љ–Њ—Б–Є—В
- –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –Љ–∞–ї–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ю—Б–љ–Њ–≤–љ–Њ–є –≤–Ї–ї–∞–і –≤ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–є –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –≤–љ–Њ—Б–Є—В  . –Ы–µ–≥–Ї–Њ –≤–Є–і–µ—В—М, —З—В–Њ –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ –≤ –і–≤–∞ —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є –Є–Љ–µ—О—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–є –Ј–љ–∞–Ї. –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Є–≤–µ—Б—В–Є —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –≤ —Д–Њ—А–Љ—Г–ї—Г (7.14) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –і–Њ–≥–Њ–≤–Њ—А–Є—В—Б—П –Њ –µ–і–Є–љ–Є—Ж–∞—Е –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Т –≥–µ–Њ—Д–Є–Ј–Є–Ї–µ –њ—А–Є–љ—П—В–Њ –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є–Ј–Љ–µ—А—П—В—М –≤ –≠—В–≤–µ—И–∞—Е, –њ–Њ –Є–Љ–µ–љ–Є –≤–µ–љ–≥–µ—А—Б–Ї–Њ–≥–Њ —Г—ЗвХ¶–љ–Њ–≥–Њ –Ы–Њ—А–∞–љ–і–∞ –≠—В–≤–µ—И–∞, –Ї–Њ—В–Њ—А—Л–є —Б–Њ–Ј–і–∞–ї –њ—А–Є–±–Њ—А –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –£—Б—В–∞–љ–Њ–≤–ї–µ–љ–Њ, —З—В–Њ –Њ–і–Є–љ –≠—В–≤–µ—И (1 –≠) —А–∞–≤–µ–љ –≥—А–∞–і–Є–µ–љ—В—Г, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ—Г 0,0001 –Љ–У–∞–ї/ –Љ –Є–ї–Є –≤ –Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–µ –µ–і–Є–љ–Є—Ж
. –Ы–µ–≥–Ї–Њ –≤–Є–і–µ—В—М, —З—В–Њ –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ –≤ –і–≤–∞ —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є –Є–Љ–µ—О—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–є –Ј–љ–∞–Ї. –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Є–≤–µ—Б—В–Є —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –≤ —Д–Њ—А–Љ—Г–ї—Г (7.14) –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –і–Њ–≥–Њ–≤–Њ—А–Є—В—Б—П –Њ –µ–і–Є–љ–Є—Ж–∞—Е –Є–Ј–Љ–µ—А–µ–љ–Є—П. –Т –≥–µ–Њ—Д–Є–Ј–Є–Ї–µ –њ—А–Є–љ—П—В–Њ –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є–Ј–Љ–µ—А—П—В—М –≤ –≠—В–≤–µ—И–∞—Е, –њ–Њ –Є–Љ–µ–љ–Є –≤–µ–љ–≥–µ—А—Б–Ї–Њ–≥–Њ —Г—ЗвХ¶–љ–Њ–≥–Њ –Ы–Њ—А–∞–љ–і–∞ –≠—В–≤–µ—И–∞, –Ї–Њ—В–Њ—А—Л–є —Б–Њ–Ј–і–∞–ї –њ—А–Є–±–Њ—А –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –£—Б—В–∞–љ–Њ–≤–ї–µ–љ–Њ, —З—В–Њ –Њ–і–Є–љ –≠—В–≤–µ—И (1 –≠) —А–∞–≤–µ–љ –≥—А–∞–і–Є–µ–љ—В—Г, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–Љ—Г 0,0001 –Љ–У–∞–ї/ –Љ –Є–ї–Є –≤ –Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–µ –µ–і–Є–љ–Є—Ж  .
.
–Я—А–µ–ґ–і–µ, —З–µ–Љ –њ—А–Є–≤–µ—Б—В–Є —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–і–µ–ї–∞–µ–Љ –µ—Й–µ –Њ–і–љ–Њ –Ј–∞–Љ–µ—З–∞–љ–Є–µ. –°–Њ –≤—А–µ–Љ–µ–љ–Є –≠—В–≤–µ—И–∞ –Њ—Б–љ–Њ–≤–љ—Л–Љ –Є–љ—Б—В—А—Г–Љ–µ–љ—В–Њ–Љ –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є —Б–ї—Г–ґ–Є—В –Ї–Њ—А–Њ–Љ—Л—Б–ї–Њ, –љ–∞ –Ї–Њ–љ—Ж–∞—Е –Ї–Њ—В–Њ—А–Њ–≥–Њ –Ј–∞–Ї—А–µ–њ–ї–µ–љ—Л –љ–∞ —А–∞–Ј–љ–Њ–є –≤—Л—Б–Њ—В–µ –Љ–∞—Б—Б—Л. –Ю—Б—М –≤—А–∞—Й–µ–љ–Є—П –Ї–Њ—А–Њ–Љ—Л—Б–ї–∞ вИЪ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–∞. –Э–µ–Њ–і–љ–Њ—А–Њ–і–љ–Њ—Б—В—М –њ–Њ–ї—П —В—П–ґ–µ—Б—В–Є —Б–Њ–Ј–і–∞вХ¶—В –Љ–Њ–Љ–µ–љ—В, –≤—А–∞—Й–∞—О—Й–Є–є –Ї–Њ—А–Њ–Љ—Л—Б–ї–Њ, –Ї–Њ—В–Њ—А—Л–є —Г—А–∞–≤–љ–Њ–≤–µ—И–Є–≤–∞–µ—В—Б—П –Љ–Њ–Љ–µ–љ—В–Њ–Љ —Г–њ—А—Г–≥–Њ–є —Б–Є–ї—Л. –Э–µ –Њ—Б—В–∞–љ–∞–≤–ї–Є–≤–∞—П—Б—М –љ–∞ –њ–Њ–і—А–Њ–±–љ–Њ—Б—В—П—Е ( —Н—В–Њ –љ–µ –њ—А–µ–і–Љ–µ—В –Њ–±—Б—Г–ґ–і–µ–љ–Є—П –і–ї—П –љ–∞—И–µ–≥–Њ –Ї—Г—А—Б–∞) —Г–Ї–∞–ґ–µ–Љ –ї–Є—И—М, —З—В–Њ —Б —Н—В–Є–Љ –њ—А–Є–±–Њ—А–Њ–Љ –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М —З–µ—В—Л—А–µ –њ–∞—А–∞–Љ–µ—В—А–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П
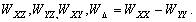 –Я—А–Є–≤–µ–івХ¶–Љ —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Њ–≥–ї–∞—Б–Њ–≤–∞–љ–љ—Л–µ —Б –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Д–Њ—А–Љ—Г–ї–Њ–є –і–ї—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є (—Б–Љ. –®–Њ–Ї–Є–љ –Я.–§. –У—А–∞–≤–Є–Љ–µ—В—А–Є—П –У–µ–Њ–і–µ–Ј–Є–Ј–і–∞—В 1960 )
–Я—А–Є–≤–µ–івХ¶–Љ —З–Є—Б–ї–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Њ–≥–ї–∞—Б–Њ–≤–∞–љ–љ—Л–µ —Б –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Д–Њ—А–Љ—Г–ї–Њ–є –і–ї—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є (—Б–Љ. –®–Њ–Ї–Є–љ –Я.–§. –У—А–∞–≤–Є–Љ–µ—В—А–Є—П –У–µ–Њ–і–µ–Ј–Є–Ј–і–∞—В 1960 )
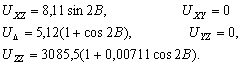 (7.15)
(7.15)
–Я—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є–Є —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ–ї—П –≤ –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ —Б–µ—А—МвХ¶–Ј–љ–Њ–є –њ–Њ–Љ–µ—Е–Њ–є —П–≤–ї—П–µ—В—Б—П –љ–µ–≤–µ—Б–Њ–Љ–Њ—Б—В—М: –њ—А–Њ–±–љ–Њ–µ —В–µ–ї–Њ –љ–µ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤—Г–µ—В —Б –Њ–њ–Њ—А–Њ–є –Є —Б–Є–ї–∞, –Ї–Њ—В–Њ—А–∞—П –і–µ–є—Б—В–≤—Г–µ—В –љ–∞ –њ—А–Њ–±–љ–Њ–µ —В–µ–ї–Њ, –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є–Ј–Љ–µ—А–µ–љ–∞. –Ю–і–љ–∞–Ї–Њ –љ–µ–≤–µ—Б–Њ–Љ–Њ—Б—В—М, —Б—В—А–Њ–≥–Њ –≥–Њ–≤–Њ—А—П, –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —В–Њ–ї—М–Ї–Њ –≤ –Њ–і–љ–Њ–є —В–Њ—З–Ї–µ –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞: –≤ —Ж–µ–љ—В—А–µ –Љ–∞—Б—Б. –Х—Б–ї–Є –њ—А–Њ–±–љ—Л–µ —В–µ–ї–∞ —А–∞–Ј–Љ–µ—Б—В–Є—В—М –≤ —А–∞–Ј–љ—Л—Е —В–Њ—З–Ї–∞—Е –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞, —В–Њ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ —Б–Є–ї—Л –±—Г–і—Г—В –і–µ–є—Б—В–≤–Њ–≤–∞—В—М –њ–Њ-—А–∞–Ј–љ–Њ–Љ—Г. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –њ–Њ–ї–Њ–ґ–µ–љ–Є—П —Н—В–Є—Е –њ—А–Њ–±–љ—Л—Е —В–µ–ї –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ–Њ–ї—Г—З–Є—В—М –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞.
–Т—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ –Њ–Ї–Њ–ї–Њ–Ј–µ–Љ–љ–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ
–Ъ–∞–Ї –Љ—Л —Г–ґ–µ –≥–Њ–≤–Њ—А–Є–ї–Є, –≥–ї–∞–≤–љ—Л–Љ –њ—А–µ–њ—П—В—Б—В–≤–Є–µ–Љ –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –±–Њ—А—В—Г –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞ —Б–ї—Г–ґ–Є—В –љ–µ–≤–µ—Б–Њ–Љ–Њ—Б—В—М. –Ю–і–љ–∞–Ї–Њ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –њ—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–∞—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М –Є–Ј–Љ–µ—А—П—В—М —Н–ї–µ–Љ–µ–љ—В—Л —В–µ–љ–Ј–Њ—А–∞ –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞.
–Я—Г—Б—В—М —В–Њ—З–Ї–∞ –† –µ—Б—В—М —В–Њ—З–Ї–∞, —Б–Њ–≤–њ–∞–і–∞—О—Й–∞—П —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–њ–њ–∞—А–∞—В–∞. –Т—Л–±–µ—А–µ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В, —Б–≤—П–Ј–∞–љ–љ—Г—О —Б –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Є–Љ –∞–њ–њ–∞—А–∞—В–Њ–Љ (—Б–Њ–њ—А–Њ–≤–Њ–ґ–і–∞—О—Й–Є–є —В—А–µ—Е–≥—А–∞–љ–љ–Є–Ї). –Э–∞—З–∞–ї–Њ —Н—В–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В –≤–Њ–Ј—М–ЉвХ¶–Љ –≤ —В–Њ—З–Ї–µ –†. –Э–∞–њ—А–∞–≤–ї–µ–љ–Є—П –Њ—Б–µ–є –≤—Л–±–µ—А–µ–Љ —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: –Њ—Б—М
Px –љ–∞–њ—А–∞–≤–Є–Љ –њ–Њ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Ї –Љ–µ—А–Є–і–Є–∞–љ—Г, –њ—А–Њ—Е–Њ–і—П—Й–µ–Љ—Г —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –†, –Њ—Б—М –†—Г - –љ–∞ –≤–Њ—Б—В–Њ–Ї , –∞ –Њ—Б—М Pz вИЪ –≤ –љ–∞—З–∞–ї–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В, —В–Њ –µ—Б—В—М –≤ —Ж–µ–љ—В—А –Ч–µ–Љ–ї–Є. –Я—Г—Б—В—М r вИЪ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А —В–Њ—З–Ї–Є –†, F
–Є L
- —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –≥–µ–Њ—Ж–µ–љ—В—А–Є—З–µ—Б–Ї–∞—П —И–Є—А–Њ—В–∞ –Є –і–Њ–ї–≥–Њ—В–∞ —Н—В–Њ–є —В–Њ—З–Ї–Є. –Ґ–Њ–≥–і–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤ —Н—В–Њ–є —В–Њ—З–Ї–µ –±—Г–і–µ—В —А–∞–≤–µ–љ
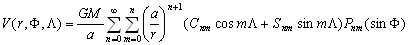 (7.16)
(7.16)
–Ч–і–µ—Б—М
 –Є
–Є  —Б—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ. –Т –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Љ—Л —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–є —З–ї–µ–љ –љ–µ —Г—З–Є—В—Л–≤–∞–µ–Љ, —В–∞–Ї –Ї–∞–Ї —А–µ—З—М –Є–і–µ—В –Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ—А–Є—В—П–ґ–µ–љ–Є—П, –∞ –љ–µ —В—П–ґ–µ—Б—В–Є.
—Б—В–Њ–Ї—Б–Њ–≤—Л –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ. –Т –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Љ—Л —Ж–µ–љ—В—А–Њ–±–µ–ґ–љ—Л–є —З–ї–µ–љ –љ–µ —Г—З–Є—В—Л–≤–∞–µ–Љ, —В–∞–Ї –Ї–∞–Ї —А–µ—З—М –Є–і–µ—В –Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ—А–Є—В—П–ґ–µ–љ–Є—П, –∞ –љ–µ —В—П–ґ–µ—Б—В–Є.
–≠–ї–µ–Љ–µ–љ—В–∞—А–љ—Л–µ –њ—А–Є—А–∞—Й–µ–љ–Є—П –і–µ–Ї–∞—А—В–Њ–≤—Л—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В, –Њ—З–µ–≤–Є–і–љ–Њ –±—Г–і—Г—В
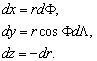 (7.17)
(7.17)
–Я–µ—А–≤—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ–Њ –Њ—Б—П–Љ —Б–Њ–њ—А–Њ–≤–Њ–ґ–і–∞—О—Й–µ–≥–Њ —В—А–µ—Е–≥—А–∞–љ–љ–Є–Ї–∞ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Њ–њ–µ—А–∞—В–Њ—А–∞
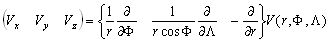 . (7.18)
. (7.18)
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ
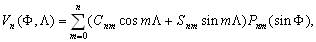
—В–µ–њ–µ—А—М —Д–Њ—А–Љ—Г–ї—Г (7.16) –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М —В–∞–Ї
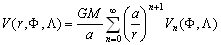 (7.19)
(7.19)
–Я–Њ–і—Б—В–∞–≤–ї—П—П –њ–Њ–ї—Г—З–µ–љ–љ—Г—О —Д–Њ—А–Љ—Г–ї—Г –≤ (7.18), –±—Г–і–µ–Љ –Є–Љ–µ—В—М –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л –≥—А–∞–і–Є–µ–љ—В–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є
r –Њ—В —Ж–µ–љ—В—А–∞ –Ч–µ–Љ–ї–Є
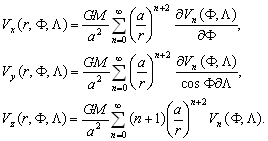 (7.20)
(7.20)
–І—В–Њ–±—Л –њ–Њ–ї—Г—З–Є—В—М –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є—В—П–ґ–µ–љ–Є—П, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ї–∞–ґ–і—Г—О –Є–Ј –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В —Б–Є–ї—Л –њ—А–Є—В—П–ґ–µ–љ–Є—П –њ—А–Њ–і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞—В—М –њ–Њ —В—АвХ¶–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –Њ—Б—П–Љ. –Я—А–Є –≤—Л—З–Є—Б–ї–µ–љ–Є–Є –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –љ–µ–ї—М–Ј—П –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —Д–Њ—А–Љ—Г–ї–∞–Љ–Є –ї–Є–љ–µ–є–љ–Њ–є —Б–≤—П–Ј–Є —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л—Е –њ—А–Є—А–∞—Й–µ–љ–Є–є –Ї–Њ–Њ—А–і–Є–љ–∞—В (7.17), –Ї–∞–Ї –Љ—Л —Н—В–Њ –і–µ–ї–∞–ї–Є –њ—А–Є –≤—Л—З–Є—Б–ї–µ–љ–Є–Є –њ–µ—А–≤—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е. –°–∞–Љ—Л–є –Њ—З–µ–≤–Є–і–љ—Л–є –њ—Г—В—М (–љ–Њ –љ–µ —Б–∞–Љ—Л–є –ївХ¶–≥–Ї–Є–є !) вИЪ –њ—А—П–Љ–Њ–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є
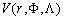 –Ї–∞–Ї –љ–µ—П–≤–љ—Г—О —Д—Г–љ–Ї—Ж–Є—О –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е x,y,z. –Ю–і–љ–∞–Ї–Њ –Њ–љ —Б–≤—П–Ј–∞–љ —Б –≥—А–Њ–Љ–Њ–Ј–і–Ї–Є–Љ–Є –≤—Л–Ї–ї–∞–і–Ї–∞–Љ–Є.
–Ї–∞–Ї –љ–µ—П–≤–љ—Г—О —Д—Г–љ–Ї—Ж–Є—О –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е x,y,z. –Ю–і–љ–∞–Ї–Њ –Њ–љ —Б–≤—П–Ј–∞–љ —Б –≥—А–Њ–Љ–Њ–Ј–і–Ї–Є–Љ–Є –≤—Л–Ї–ї–∞–і–Ї–∞–Љ–Є.
–Э–∞—И–∞ —Ж–µ–ї—М вИЪ –њ–Њ–Ї–∞–Ј–∞—В—М –Ї–∞–Ї –Є–Ј–Љ–µ–љ—П—О—В—Б—П –≤—В–Њ—А—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є—П –і–Њ —Б–њ—Г—В–љ–Є–Ї–∞. –Я–Њ—Н—В–Њ–Љ—Г –Њ–≥—А–∞–љ–Є—З–Є–Љ—Б—П –ї–Є—И—М –≤—В–Њ—А–Њ–є —А–∞–і–Є–∞–ї—М–љ–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –°–Є–ї–Њ–≤–∞—П –ї–Є–љ–Є—П –і–ї—П —Н—В–Њ–є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л вИЪ –њ—А—П–Љ–∞—П –ї–Є–љ–Є—П, –њ–Њ—Н—В–Њ–Љ—Г —Г—З–Є—В—Л–≤–∞—В—М –µвХ¶ –Ї—А–Є–≤–Є–Ј–љ—Г –љ–µ —В—А–µ–±—Г–µ—В—Б—П. –Ф–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї, –Ј–∞–і–∞–љ–љ—Л–є —Д–Њ—А–Љ—Г–ї–Њ–є (7.19), –њ–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В–µ
r, –њ–Њ–ї—Г—З–Є–Љ
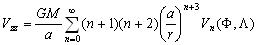 (7.21)
(7.21)
–Ь—Л –≤–Є–і–Є–Љ, —З—В–Њ –њ–Њ—Б–ї–µ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є—П –Ї–∞–ґ–і—Л–є —З–ї–µ–љ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є–Њ–±—А–µ—В–∞–µ—В –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, —А–∞—Б—В—Г—Й–Є–є —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ —Б—В–µ–њ–µ–љ–Є –Ї–∞–Ї
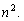 –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Љ–љ–Њ–ґ–Є—В–µ–ї—М(
–њ+1)(–њ+2) , —Г–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ —Б –њ–Њ–≤—Л—И–µ–љ–Є–µ–Љ вМ†—З–∞—Б—В–Њ—В—ЛвЦ† —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –Є –Љ–љ–Њ–ґ–Є—В–µ–ї—М, —В–Њ—З–љ–Њ —В–∞–Ї –ґ–µ, –Ї–∞–Ї –Є –њ—А–Є —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–Љ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–Є —Д—Г–љ–Ї—Ж–Є–Є –≤—А–µ–Љ–µ–љ–Є. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г—О—Й–Є–є —Н—Д—Д–µ–Ї—В —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В вМ†–≤–µ—А—Е–љ–Є–µвЦ† –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Љ–љ–Њ–ґ–Є—В–µ–ї—М(
–њ+1)(–њ+2) , —Г–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ —Б –њ–Њ–≤—Л—И–µ–љ–Є–µ–Љ вМ†—З–∞—Б—В–Њ—В—ЛвЦ† —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –Є –Љ–љ–Њ–ґ–Є—В–µ–ї—М, —В–Њ—З–љ–Њ —В–∞–Ї –ґ–µ, –Ї–∞–Ї –Є –њ—А–Є —Б–њ–µ–Ї—В—А–∞–ї—М–љ–Њ–Љ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–Є —Д—Г–љ–Ї—Ж–Є–Є –≤—А–µ–Љ–µ–љ–Є. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г—О—Й–Є–є —Н—Д—Д–µ–Ї—В —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В вМ†–≤–µ—А—Е–љ–Є–µвЦ† –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞.
–Ю–і–љ–∞–Ї–Њ, –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —Б —Н—В–Є–Љ —Н—Д—Д–µ–Ї—В–Њ–Љ —Б—Г—Й–µ—Б—В–≤—Г–µ—В –Є вМ†–Є–љ—В–µ–≥—А–Є—А—Г—О—Й–Є–євЦ† —Н—Д—Д–µ–Ї—В: —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є—П
r –Љ–љ–Њ–ґ–Є—В–µ–ї—М 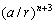 —Г–Љ–µ–љ—М—И–∞–µ—В –∞–Љ–њ–ї–Є—В—Г–і—Г –≥–∞—А–Љ–Њ–љ–Є–Ї–Є. –Я–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ–њ—А–Њ—Б, –Ї–∞–Ї–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –Є –љ–∞ –Ї–∞–Ї–Њ–є –≤—Л—Б–Њ—В–µ —Б–ї–µ–і—Г–µ—В –Њ–њ—А–µ–і–µ–ї—П—В—М –њ—А–Є –њ–ї–∞–љ–Є—А–Њ–≤–∞–љ–Є–Є –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞.
—Г–Љ–µ–љ—М—И–∞–µ—В –∞–Љ–њ–ї–Є—В—Г–і—Г –≥–∞—А–Љ–Њ–љ–Є–Ї–Є. –Я–Њ—Н—В–Њ–Љ—Г –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ–њ—А–Њ—Б, –Ї–∞–Ї–Є–µ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –Є –љ–∞ –Ї–∞–Ї–Њ–є –≤—Л—Б–Њ—В–µ —Б–ї–µ–і—Г–µ—В –Њ–њ—А–µ–і–µ–ї—П—В—М –њ—А–Є –њ–ї–∞–љ–Є—А–Њ–≤–∞–љ–Є–Є –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞.
–Р–љ–≥–ї–Є–є—Б–Ї–Є–є —Г—ЗвХ¶–љ—Л–є –Ъ–∞—Г–ї–∞ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ –њ–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ –∞–Љ–њ–ї–Є—В—Г–і—Л —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Г–±—Л–≤–∞—О—В —Б –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є–µ–Љ —Б—В–µ–њ–µ–љ–Є –њ –Ї–∞–Ї
 . –° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л –∞–Љ–њ–ї–Є—В—Г–і—Л –≥–∞—А–Љ–Њ–љ–Є–Ї –≤—В–Њ—А–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –Ї–∞–Ї
. –° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л –∞–Љ–њ–ї–Є—В—Г–і—Л –≥–∞—А–Љ–Њ–љ–Є–Ї –≤—В–Њ—А–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В—Б—П –Ї–∞–Ї  . –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≤ —И–Є—А–Њ–Ї–Њ–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–µ —З–∞—Б—В–Њ—В –Є–Љ–µ—О—В —Е–∞—А–∞–Ї—В–µ—А вМ†–±–µ–ї–Њ–≥–Њ —И—Г–Љ–∞вЦ†. –Э–Њ —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –≤—Л—Б–Њ—В—Л –±–ї–∞–≥–Њ–і–∞—А—П –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ—Г —Н—Д—Д–µ–Ї—В—Г –≤–µ—А—Е–љ–Є–є –і–Є–∞–њ–∞–Ј–Њ–љ —З–∞—Б—В–Њ—В –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –њ–Њ–і–∞–≤–ї–µ–љ–љ—Л–Љ.
. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≤ —И–Є—А–Њ–Ї–Њ–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–µ —З–∞—Б—В–Њ—В –Є–Љ–µ—О—В —Е–∞—А–∞–Ї—В–µ—А вМ†–±–µ–ї–Њ–≥–Њ —И—Г–Љ–∞вЦ†. –Э–Њ —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –≤—Л—Б–Њ—В—Л –±–ї–∞–≥–Њ–і–∞—А—П –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ—Г —Н—Д—Д–µ–Ї—В—Г –≤–µ—А—Е–љ–Є–є –і–Є–∞–њ–∞–Ј–Њ–љ —З–∞—Б—В–Њ—В –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –њ–Њ–і–∞–≤–ї–µ–љ–љ—Л–Љ.
–Т—Л–њ–Њ–ї–љ–Є–Љ –њ—А–Њ—Б—В–µ–є—И–Є–є —А–∞—Б—ЗвХ¶—В вМ†—З–∞—Б—В–Њ—В–љ–Њ–є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–ЄвЦ† –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤ –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —А–∞–і–Є–∞–ї—М–љ–Њ–є –≤—В–Њ—А–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –љ–∞ –≤—Л—Б–Њ—В–µ
h.
–Я—Г—Б—В—М
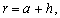 –≥–і–µ h - –≤—Л—Б–Њ—В–∞ –њ–Њ–ївХ¶—В–∞ —Б–њ—Г—В–љ–Є–Ї–∞ –љ–∞–і –њ–ї–∞–љ–µ—В–Њ–є. –Т –Ї–∞—З–µ—Б—В–≤–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –њ–Њ–і–∞–≤–ї–µ–љ–Є—П –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —Б—В–µ–њ–µ–љ–Є –њ, –Њ—З–µ–≤–Є–і–љ–Њ, –Љ–Њ–ґ–љ–Њ –њ—А–Є–љ—П—В—М
–≥–і–µ h - –≤—Л—Б–Њ—В–∞ –њ–Њ–ївХ¶—В–∞ —Б–њ—Г—В–љ–Є–Ї–∞ –љ–∞–і –њ–ї–∞–љ–µ—В–Њ–є. –Т –Ї–∞—З–µ—Б—В–≤–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –њ–Њ–і–∞–≤–ї–µ–љ–Є—П –≥–∞—А–Љ–Њ–љ–Є–Ї–Є —Б—В–µ–њ–µ–љ–Є –њ, –Њ—З–µ–≤–Є–і–љ–Њ, –Љ–Њ–ґ–љ–Њ –њ—А–Є–љ—П—В—М
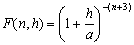
–Я—А–Є–≤–µ–івХ¶–Љ —В–∞–±–ї–Є—Ж—Г –Ј–љ–∞—З–µ–љ–Є–є
F(n,h) –њ—А–Є —А–∞–Ј–ї–Є—З–љ—Л—Е –≤—Л—Б–Њ—В–∞—Е –Є —Б—В–µ–њ–µ–љ–µ–є –≥–∞—А–Љ–Њ–љ–Є–Ї.
|
–њ \ h |
200 –Ї–Љ |
500 –Ї–Љ |
1000 –Ї–Љ |
5000 –Ї–Љ |
|
2 |
0.86 |
0.68 |
0.48 |
0.055 |
|
4 |
0.80 |
0.59 |
0.36 |
0.017 |
|
6 |
0.76 |
0.51 |
0.27 |
0.005 |
|
8 |
0.71 |
0.44 |
0.20 |
- |
|
10 |
0.67 |
0.37 |
0.15 |
- |
|
20 |
0.49 |
0.18 |
0.035 |
- |
|
50 |
0.19 |
0.018 |
- |
- |
|
100 |
0.041 |
- |
- |
- |
–Ґ–∞–±–ї–Є—Ж–∞ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –Ј–∞–і–∞—З–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –≥–Њ–і—П—В—Б—П –ї–Є—И—М –Њ—З–µ–љ—М –љ–Є–Ј–Ї–Є–µ —Б–њ—Г—В–љ–Є–Ї–Є. –Я—А–Є—ЗвХ¶–Љ –љ–∞ –≤—Л—Б–Њ—В–µ 200 –Ї–Љ –Њ—В –≥–∞—А–Љ–Њ–љ–Є–Ї —Б—В–µ–њ–µ–љ–Є –Є –њ–Њ—А—П–і–Ї–∞ 100 –Њ—Б—В–∞вХ¶—В—Б—П –ї–Є—И—М –Њ–Ї–Њ–ї–Њ 4%. –≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –µ—Б–ї–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є –љ–∞—Б –Љ–Њ–ґ–µ—В —Г–і–Њ–≤–ї–µ—В–≤–Њ—А–Є—В—М —В–Њ—З–љ–Њ—Б—В—М 1% –Њ—В –∞–Љ–њ–ї–Є—В—Г–і—Л –∞–љ–Њ–Љ–∞–ї–Є–є –≥—А–∞–і–Є–µ–љ—В–∞, —В–Њ –≤ –Ї–Њ—Б–Љ–Є—З–µ—Б–Ї–Є—Е —Г—Б–ї–Њ–≤–Є—П—Е –Љ—Л –±—Г–і–µ–Љ –≤—Л–љ—Г–ґ–і–µ–љ—Л —В—А–µ–±–Њ–≤–∞—В—М —В–Њ—З–љ–Њ—Б—В—М –љ–∞ –і–≤–∞ –њ–Њ—А—П–і–Ї–∞ –≤—Л—И–µ. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤ –Ї–∞—З–µ—Б—В–≤–µ –њ—А–Є–µ–Љ–ї–µ–Љ–Њ–є —В–Њ—З–љ–Њ—Б—В–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П –Љ—Л –і–Њ–ї–ґ–љ—Л –њ–ї–∞–љ–Є—А–Њ–≤–∞—В—М —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В—М –њ—А–Є–±–Њ—А–Њ–≤ –љ–µ –Љ–µ–љ–µ–µ 0,001–≠, —З—В–Њ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ –≥—А–∞–і–Є–µ–љ—В—Г
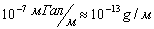 . –Ґ–∞–Ї–Њ–є –≤—Л—Б–Њ–Ї–Њ–є —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В–Є –≤ –Ј–µ–Љ–љ—Л—Е —Г—Б–ї–Њ–≤–Є—П—Е –≤—А—П–і –ї–Є –Љ–Њ–ґ–љ–Њ –і–Њ—Б—В–Є–≥–љ—Г—В—М. –Ю–і–љ–∞–Ї–Њ –≤ –Ї–Њ—Б–Љ–Њ—Б–µ, –≤ —Г—Б–ї–Њ–≤–Є—П—Е –≥–ї—Г–±–Њ–Ї–Њ–≥–Њ –≤–∞–Ї—Г—Г–Љ–∞ –Є —Б–≤–µ—А—Е–љ–Є–Ј–Ї–Є—Е —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞—Е –љ–∞–і–µ–ґ–і–∞ –љ–∞ —Г—Б–њ–µ—Е –Њ—Б—В–∞вХ¶—В—Б—П.
. –Ґ–∞–Ї–Њ–є –≤—Л—Б–Њ–Ї–Њ–є —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В–Є –≤ –Ј–µ–Љ–љ—Л—Е —Г—Б–ї–Њ–≤–Є—П—Е –≤—А—П–і –ї–Є –Љ–Њ–ґ–љ–Њ –і–Њ—Б—В–Є–≥–љ—Г—В—М. –Ю–і–љ–∞–Ї–Њ –≤ –Ї–Њ—Б–Љ–Њ—Б–µ, –≤ —Г—Б–ї–Њ–≤–Є—П—Е –≥–ї—Г–±–Њ–Ї–Њ–≥–Њ –≤–∞–Ї—Г—Г–Љ–∞ –Є —Б–≤–µ—А—Е–љ–Є–Ј–Ї–Є—Е —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞—Е –љ–∞–і–µ–ґ–і–∞ –љ–∞ —Г—Б–њ–µ—Е –Њ—Б—В–∞вХ¶—В—Б—П.
–Ы–µ–Ї—Ж–Є—П 8
–Т–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї, –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є. –Ъ—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –і–ї—П –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Т–љ–µ—И–љ–Є–µ –Є –≤–љ—Г—В—А–µ–љ–љ–Є–µ –Ї—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є –Ф–Є—А–Є—Е–ї–µ, –Э–µ–є–Љ–∞–љ–∞, —Б–Љ–µ—И–∞–љ–љ—Л–µ –Ї—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є. –Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –≤—Л—Б–Њ—В –≥–µ–Њ–Є–і–∞ –Љ–µ—В–Њ–і–Њ–Љ –°—В–Њ–Їc–∞. –§—Г–љ–Ї—Ж–Є—П –°—В–Њ–Ї—Б–∞. –Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Г–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–∞. –§–Њ—А–Љ—Г–ї—Л –Т–µ–љ–Є–љ–≥-–Ь–µ–є–љ–µ—Б–∞.
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Д–Є–≥—Г—А—Л –≥–µ–Њ–Є–і–∞
–Т–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї
–°—А–µ–і–Є —Б–њ–µ—Ж–Є–∞–ї–Є—Б—В–Њ–≤ –њ–Њ –≤—Л—Б–µ–є –≥–µ–Њ–і–µ–Ј–Є–Є —И–Є—А–Њ–Ї–Њ –њ—А–Є–Љ–µ–љ—П–µ—В—Б—П —В–µ—А–Љ–Є–љ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї, –Ї–∞–Ї —А–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г —А–µ–∞–ї—М–љ—Л–Љ –Є –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞–Љ–Є –≤ –Њ–і–љ–Њ–є —В–Њ—З–Ї–µ. –Э–µ–ї—М–Ј—П —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ —В–µ—А–Љ–Є–љ —Г–і–∞—З–µ–љ. –Т –љ–µ–±–µ—Б–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–µ —З–∞—Б—В–Њ —Г–њ–Њ—В—А–µ–±–ї—П–µ—В—Б—П —В–µ—А–Љ–Є–љ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–µ —Б–Є–ї—Л, –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–∞—П —Б–Є–ї–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, –≤–Њ–Ј–Љ—Г—Й–µ–љ–Є—П. –Т–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ–њ—А–Њ—Б, —З—В–Њ –Є–Љ–µ–љ–љ–Њ –≤–Њ–Ј–Љ—Г—Й–∞–µ—В –і–∞–љ–љ–∞—П —Б–Є–ї–∞? –Ф–ї—П –љ–µ–±–µ—Б–љ–Њ–є –Љ–µ—Е–∞–љ–Є–Ї–Є –Њ—В–≤–µ—В —П—Б–µ–љ вИЪ –Ј–∞–Ї–Њ–љ –і–≤–Є–ґ–µ–љ–Є—П —В–µ–ї–∞, –і–µ–ї–∞–µ—В –µ–≥–Њ –Њ—В–ї–Є—З–љ—Л–Љ –Њ—В –Ї–µ–њ–ї–µ—А–Њ–≤—Б–Ї–Њ–≥–Њ, –љ–µ–≤–Њ–Ј–Љ—Г—ЙвХ¶–љ–љ–Њ–≥–Њ. –Я—А–∞–≤–і–∞, —В–µ—А–Љ–Є–љ–Њ–ї–Њ–≥–Є—П –Љ–Њ—Б–Ї–Њ–≤—Б–Ї–Њ–є –Є –њ–µ—В–µ—А–±—Г—А–≥—Б–Ї–Њ–є —И–Ї–Њ–ї –љ–µ–±–µ—Б–љ—Л—Е –Љ–µ—Е–∞–љ–Є–Ї–Њ–≤ —А–∞–Ј–ї–Є—З–∞—О—В—Б—П. –Ь–Њ—Б–Ї–≤–Є—З–Є –≥–Њ–≤–Њ—А—П—В —Д—Г–љ–Ї—Ж–Є—П –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–∞—П, –∞ –њ–µ—В–µ—А–±—Г—А–ґ—Ж—Л вИЪ –њ–µ—А—В—Г—А–±–∞—Ж–Є–Њ–љ–љ–∞—П. –Ґ–∞–Ї —З—В–Њ –ґ–µ вМ†–≤–Њ–Ј–Љ—Г—Й–∞–µ—ВвЦ† –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї? –Ю—В–≤–µ—В вИЪ –љ–Є—З–µ–≥–Њ. –Я–Њ-–≤–Є–і–Є–Љ–Њ–Љ—Г –њ—А–∞–≤ –∞–≤—Б—В—А–Є–є—Б–Ї–Є–є –≥–µ–Њ–і–µ–Ј–Є—Б—В –У.–Ь–Њ—А–Є—Ж, –Ї–Њ—В–Њ—А—Л–є –њ—А–µ–і–ї–∞–≥–∞–µ—В –≤–≤–µ—Б—В–Є —В–µ—А–Љ–Є–љ –∞–љ–Њ–Љ–∞–ї–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞. –У–Њ–≤–Њ—А–Є–Љ –ґ–µ –Љ—Л –∞–љ–Њ–Љ–∞–ї–Є—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –Є–Љ–µ—П –≤ –≤–Є–і—Г —А–∞–Ј–љ–Њ—Б—В—М —А–µ–∞–ї—М–љ–Њ–є –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є! –Э–Њ –Њ—В–і–∞–≤–∞—П –і–∞–љ—М —В—А–∞–і–Є—Ж–Є–Є, –Љ—Л –±—Г–і–µ–Љ —Г–њ–Њ—В—А–µ–±–ї—П—В—М —В–µ—А–Љ–Є–љ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –Є–Љ–µ–љ–љ–Њ –Ї–∞–Ї —А–∞–Ј–љ–Њ—Б—В—М —А–µ–∞–ї—М–љ–Њ–≥–Њ –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤ —В—П–ґ–µ—Б—В–Є –Є–ї–Є –њ—А–Є—В—П–ґ–µ–љ–Є—П –≤–Ј—П—В—Л—Е –≤ –Њ–і–љ–Њ–є –Є —В–Њ–є –ґ–µ —В–Њ—З–Ї–µ.
–Т–Њ–Ј—М–ЉвХ¶–Љ —В–Њ—З–Ї—Г –†
–љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≥–µ–Њ–Є–і–∞ вИЪ —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є вИЪ —Б –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є N , B, L., –≥–і–µ N - –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П –≤—Л—Б–Њ—В–∞ —В–Њ—З–Ї–Є (—А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –і–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ ) –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є —Н—В–Њ –≤—Л—Б–Њ—В–∞ –≥–µ–Њ–Є–і–∞ –≤ —В–Њ—З–Ї–µ –†. –Ф–≤–µ –і—А—Г–≥–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л - B –Є L —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ —И–Є—А–Њ—В–∞ –Є –і–Њ–ї–≥–Њ—В–∞ (—Б–Љ. –ї–µ–Ї—Ж–Є—О 2) –Э–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —В–Њ—З–Ї—Г —Б —В–∞–Ї–Є–Љ–Є –ґ–µ –Ј–љ–∞—З–µ–љ–Є—П–Љ–Є —И–Є—А–Њ—В—Л –Є –і–Њ–ї–≥–Њ—В—Л –±—Г–і–µ–Љ –Њ–±–Њ–Ј–љ–∞—З–∞—В—М –±—Г–Ї–≤–Њ–є Q. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ –≤—Л—Б–Њ—В–∞ —Н—В–Њ–є —В–Њ—З–Ї–Є —А–∞–≤–љ–∞ –љ—Г–ї—О. –°–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –≤ —В–Њ—З–Ї–µ –†:

–Э–Њ—А–Љ–∞–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –≤ —В–Њ—З–Ї–µ
Q:
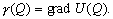
–†–∞–Ј–љ–Њ—Б—В—М –∞–±—Б–Њ–ї—О—В–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є —Н—В–Є—Е –≤–µ–Ї—В–Њ—А–Њ–≤ –Њ–њ—А–µ–і–µ–ї—П–µ—В —Б–Љ–µ—И–∞–љ–љ—Г—О –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О
.
–Т–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤ —В–Њ—З–Ї–µ
Q (–љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ) —А–∞–≤–µ–љ
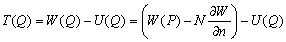
–Ю–і–љ–∞–Ї–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г
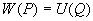 , –њ–Њ–ї—Г—З–Є–Љ
, –њ–Њ–ї—Г—З–Є–Љ
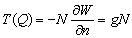 (8.1)
(8.1)
–Ю–њ—А–µ–і–µ–ї–Є–Љ —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О
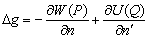 (8.2)
(8.2)
–Т –њ–µ—А–≤–Њ–Љ —Б–ї–∞–≥–∞–µ–Љ–Њ–Љ –Љ—Л –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А—Г–µ–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї –њ–Њ –≤–љ–µ—И–љ–µ–є –љ–Њ—А–Љ–∞–ї–Є –Ї –≥–µ–Њ–Є–і—Г, –∞ –≤–Њ –≤—В–Њ—А–Њ–Љ вИЪ –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г. –≠—В–Є –і–≤–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П, –≤–Њ–Њ–±—Й–µ –≥–Њ–≤–Њ—А—П, –љ–µ —Б–Њ–≤–њ–∞–і–∞—О—В. –Я—А–∞–≤–і–∞, –Њ—В–ї–Є—З–Є–µ –љ–µ –≤–µ–ї–Є–Ї–Њ –Є
–Њ—И–Є–±–Ї–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В –≤—Б–µ–≥–Њ  , —В–Њ –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ—Г –њ–Њ—А—П–і–Ї–∞ –Ї–≤–∞–і—А–∞—В–∞ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є. –≠—В–Њ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –Љ–µ–љ—М—И–µ –Ї–≤–∞–і—А–∞—В–∞ —Б–ґ–∞—В–Є—П, –њ–Њ—Н—В–Њ–Љ—Г –≤ –љ–∞—И–µ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–Є –Љ–Њ–ґ–љ–Њ –љ–µ –і–µ–ї–∞—В—М —А–∞–Ј–ї–Є—З–Є—П –≤ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П—Е –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є –Є –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г.
, —В–Њ –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ—Г –њ–Њ—А—П–і–Ї–∞ –Ї–≤–∞–і—А–∞—В–∞ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є. –≠—В–Њ —Б—Г—Й–µ—Б—В–≤–µ–љ–љ–Њ –Љ–µ–љ—М—И–µ –Ї–≤–∞–і—А–∞—В–∞ —Б–ґ–∞—В–Є—П, –њ–Њ—Н—В–Њ–Љ—Г –≤ –љ–∞—И–µ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–Є –Љ–Њ–ґ–љ–Њ –љ–µ –і–µ–ї–∞—В—М —А–∞–Ј–ї–Є—З–Є—П –≤ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П—Е –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є –Є –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г.
"
–Ю–њ—Г—Б—В–Є–Љ" –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є–Ј —В–Њ—З–Ї–Є –† –≤ —В–Њ—З–Ї—Г Q, –њ—А–Є–Љ–µ–љ—П—П —Д–Њ—А–Љ—Г–ї—Л –ї–Є–љ–µ–є–љ–Њ–≥–Њ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є—П
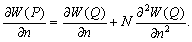 (8.3)
(8.3)
–Т–µ—А—В–Є–Ї–∞–ї—М–љ—Л–є –≥—А–∞–і–Є–µ–љ—В —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –Ї–∞–Ї –Љ—Л –≤–Є–і–µ–ї–Є (—Б–Љ. –ї–µ–Ї—Ж–Є—О 7), –Ј–∞–≤–Є—Б–Є—В –Њ—В —А–∞–і–Є—Г—Б–Њ–≤ –Ї—А–Є–≤–Є–Ј–љ—Л –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Б–µ—З–µ–љ–Є–є –Є —Г–≥–ї–Њ–≤–Њ–є —Б–Ї–Њ—А–Њ—Б—В–Є –≤—А–∞—Й–µ–љ–Є—П –Ч–µ–Љ–ї–Є
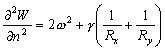 .
.
–Я—А–µ–љ–µ–±—А–µ–≥–∞—П –Љ–∞–ї—Л–Љ–Є –њ–Њ—А—П–і–Ї–∞
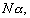 –Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М –Є —З–ї–µ–љ–Њ–Љ
–Љ–Њ–ґ–љ–Њ –њ—А–µ–љ–µ–±—А–µ—З—М –Є —З–ї–µ–љ–Њ–Љ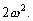 –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г N —В–∞–Ї–ґ–µ –Љ–∞–ї–∞—П –≤–µ–ї–Є—З–Є–љ–∞ (—Б—А–∞–≤–љ–µ–љ–Є—О —Б R), –Љ–Њ–ґ–љ–Њ –љ–µ —Г—З–Є—В—Л–≤–∞—В—М —А–∞–Ј–ї–Є—З–Є—П –Љ–µ–ґ–і—Г —А–∞–і–Є—Г—Б–∞–Љ–Є –Ї—А–Є–≤–Є–Ј–љ—Л –Љ–µ—А–Є–і–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П –Є —Б–µ—З–µ–љ–Є—П –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї–µ. –Я–Њ—Б–ї–µ —Г–њ—А–Њ—Й–µ–љ–Є–є, —Д–Њ—А–Љ—Г–ї–∞ (8.3) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і:
–Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г N —В–∞–Ї–ґ–µ –Љ–∞–ї–∞—П –≤–µ–ї–Є—З–Є–љ–∞ (—Б—А–∞–≤–љ–µ–љ–Є—О —Б R), –Љ–Њ–ґ–љ–Њ –љ–µ —Г—З–Є—В—Л–≤–∞—В—М —А–∞–Ј–ї–Є—З–Є—П –Љ–µ–ґ–і—Г —А–∞–і–Є—Г—Б–∞–Љ–Є –Ї—А–Є–≤–Є–Ј–љ—Л –Љ–µ—А–Є–і–Є–Њ–љ–∞–ї—М–љ–Њ–≥–Њ —Б–µ—З–µ–љ–Є—П –Є —Б–µ—З–µ–љ–Є—П –≤ –њ–µ—А–≤–Њ–Љ –≤–µ—А—В–Є–Ї–∞–ї–µ. –Я–Њ—Б–ї–µ —Г–њ—А–Њ—Й–µ–љ–Є–є, —Д–Њ—А–Љ—Г–ї–∞ (8.3) –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і:
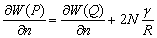 (8.4)
(8.4)
–Ґ–µ–њ–µ—А—М —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
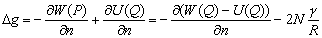 .
.
–†–∞–Ј–љ–Њ—Б—В—М
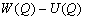 –µ—Б—В—М –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤ —В–Њ—З–Ї–µ Q, –∞ —В–Њ—В, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, —Б–≤—П–Ј–∞–љ —Б –≤—Л—Б–Њ—В–Њ–є –≥–µ–Њ–Є–і–∞ N —Д–Њ—А–Љ—Г–ї–Њ–є (8.1). –Ч–∞–Љ–µ–љ—П—П –≤ —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї–µ —А–µ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ, –њ–Њ–ї—Г—З–Є–Љ
–µ—Б—В—М –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤ —В–Њ—З–Ї–µ Q, –∞ —В–Њ—В, –≤ —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, —Б–≤—П–Ј–∞–љ —Б –≤—Л—Б–Њ—В–Њ–є –≥–µ–Њ–Є–і–∞ N —Д–Њ—А–Љ—Г–ї–Њ–є (8.1). –Ч–∞–Љ–µ–љ—П—П –≤ —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї–µ —А–µ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ, –њ–Њ–ї—Г—З–Є–Љ 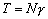 . –Ґ–µ–њ–µ—А—М —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М —З–µ—А–µ–Ј –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
. –Ґ–µ–њ–µ—А—М —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М —З–µ—А–µ–Ј –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
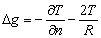 (8.5)
(8.5)
–Ш—В–∞–Ї, –Ј–∞–і–∞—З–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д–Є–≥—Г—А—Л –≥–µ–Њ–Є–і–∞ (–њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞) —Б–≤–Њ–і–Є—В—Б—П –Ї –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Ґ вИЪ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –Ї–Њ—В–Њ—А—Л–є –ї–Є–љ–µ–є–љ–Њ —Б–≤—П–Ј–∞–љ —Б –≤—Л—Б–Њ—В–Њ–є –≥–µ–Њ–Є–і–∞. –Я—А–Њ–±–ї–µ–Љ–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞, –њ—А–Є —Г—Б–ї–Њ–≤–Є–Є, —З—В–Њ –љ–∞ –Ј–∞–і–∞–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є—Б–Ї–Њ–Љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–Њ–і—З–Є–љ—П–µ—В—Б—П –љ–µ–Ї–Њ—В–Њ—А–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є—О, –Ї–Њ—В–Њ—А–Њ–µ –љ–∞–Ј—Л–≤–∞—О—В –Ї—А–∞–µ–≤—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ, –њ—А–Є–љ–∞–і–ї–µ–ґ–Є—В –Ї –±–Њ–ї—М—И–Њ–Љ—Г –Ї–ї–∞—Б—Б—Г –Ї—А–∞–µ–≤—Л—Е –Ј–∞–і–∞—З, —Б –љ–µ–Ї–Њ—В–Њ—А—Л–Љ–Є –Є–Ј –љ–Є—Е –Љ—Л –Є –њ–Њ–Ј–љ–∞–Ї–Њ–Љ–Є–Љ—Б—П.
–Ъ—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –Ф–Є—А–Є—Е–ї–µ –і–ї—П —Б—Д–µ—А—Л
–Я–Њ–њ—Л—В–∞–µ–Љ—Б—П —А–µ—И–Є—В—М —Б–ї–µ–і—Г—О—Й—Г—О –Ј–∞–і–∞—З—Г. –Ф–∞–љ–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ы–∞–њ–ї–∞—Б–∞, –Њ–њ—А–µ–і–µ–ї—П—О—Й–µ–µ —Д—Г–љ–Ї—Ж–Є—О G(P), –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї—Г—О –≤ –љ–µ–Ї–Њ—В–Њ—А–Њ–є –Њ–±–ї–∞—Б—В–Є, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–є –Ј–∞–Љ–Ї–љ—Г—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О S. –Т—Б–µ –Ј–љ–∞—З–µ–љ–Є—П —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –љ–∞ –≥—А–∞–љ–Є—Ж–µ –Њ–±–ї–∞—Б—В–Є, —В–Њ –µ—Б—В—М –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є S, –Є–Ј–≤–µ—Б—В–љ—Л. –Ш–Ј –≤—Б–µ—Е —А–µ—И–µ–љ–Є–є —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞ —В—А–µ–±—Г–µ—В—Б—П –≤—Л–±—А–∞—В—М —В–Њ–ї—М–Ї–Њ —В–µ, –Ї–Њ—В–Њ—А—Л–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—В –Ї—А–∞–µ–≤–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є—О. –†–µ—И–µ–љ–Є–µ —Н—В–Њ–є –Ј–∞–і–∞—З–Є —Б—Г—Й–µ—Б—В–≤–µ–љ–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –Ј–∞–≤–Є—Б–Є—В –Њ—В –≤–Є–і–∞ –≥—А–∞–љ–Є—З–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Я–Њ–Ї–∞–ґ–µ–Љ, –Ї–∞–Ї –Њ–љ–∞ —А–µ—И–∞–µ—В—Б—П, –µ—Б–ї–Є –Ј–∞–і–∞–љ–љ–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М вИЪ —Б—Д–µ—А–∞. –Т –і–∞–љ–љ–Њ–є —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї–µ –Є–Љ–µ–µ–Љ –і–µ–ї–Њ —Б –≤–љ—Г—В—А–µ–љ–љ–µ–є –њ—А–Њ–±–ї–µ–Љ–Њ–є –Ф–Є—А–Є—Е–ї–µ.
–Ш–љ–Њ–≥–і–∞ —В—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї—Г—О —Д—Г–љ–Ї—Ж–Є—О –≤–љ–µ –≥—А–∞–љ–Є—З–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ґ–Њ–≥–і–∞ —Н—В–Њ –≤–љ–µ—И–љ—П—П –њ—А–Њ–±–ї–µ–Љ–∞ –Ф–Є—А–Є—Е–ї–µ
.
–Ф–Њ–њ—Г—Б—В–Є–Љ, —З—В–Њ –Є—Б–Ї–Њ–Љ–∞—П —Д—Г–љ–Ї—Ж–Є—П
G(P) –Ј–∞–і–∞–љ–∞ –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л S
–Ј–љ–∞—З–µ–љ–Є—П–Љ–Є
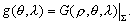
–†–∞–Ј–ї–Њ–ґ–Є–Љ —Д—Г–љ–Ї—Ж–Є—О
 –≤ —А—П–і –Ы–∞–њ–ї–∞—Б–∞:
–≤ —А—П–і –Ы–∞–њ–ї–∞—Б–∞: 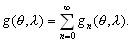
|
–Т–љ—Г—В—А–µ–љ–љ—П—П –њ—А–Њ–±–ї–µ–Љ–∞ –Ф–Є—А–Є—Е–ї–µ |
–Т–љ–µ—И–љ—П—П –њ—А–Њ–±–ї–µ–Љ–∞ –Ф–Є—А–Є—Е–ї–µ |
|
–Ш—Б–Ї–Њ–Љ—Л–Љ —А–µ—И–µ–љ–Є–µ–Љ –±—Г–і–µ—В |
–†–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞ –Ј–∞–і–∞—О—В –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ |
|
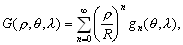 (8.6) (8.6)
|
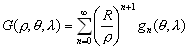 (8.6) (8.6)
|
|
—В–∞–Ї –Ї–∞–Ї
- —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞ –Ї–∞–Ї —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞.
- –љ–∞ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —А–∞–і–Є—Г—Б–∞
R –Њ–љ–∞ —А–∞–≤–љ–∞ g(q
,l
).
|
–≠—В–∞ —Д—Г–љ–Ї—Ж–Є—П —В–∞–Ї–ґ–µ
- —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—А–∞–≤–љ–µ–љ–Є—О –Ы–∞–њ–ї–∞—Б–∞ –Ї–∞–Ї —И–∞—А–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞,
- –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ–љ–∞ —А–∞–≤–љ–∞
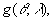 –љ–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є —Б—В—А–µ–Љ–Є—В—Б—П –Ї –љ—Г–ї—О –Ї–∞–Ї
–љ–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є —Б—В—А–µ–Љ–Є—В—Б—П –Ї –љ—Г–ї—О –Ї–∞–Ї  , —З—В–Њ –≥–Њ–≤–Њ—А–Є—В –Њ –µвХ¶ —А–µ–≥—Г–ї—П—А–љ–Њ—Б—В–Є –љ–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є.
, —З—В–Њ –≥–Њ–≤–Њ—А–Є—В –Њ –µвХ¶ —А–µ–≥—Г–ї—П—А–љ–Њ—Б—В–Є –љ–∞ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є. |
–Ъ—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є –Э–µ–є–Љ–∞–љ–∞
–Э–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є–љ–Њ–≥–і–∞ –Ј–∞–і–∞–љ—Л –љ–µ –Ј–љ–∞—З–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є, –∞ –µвХ¶ –љ–Њ—А–Љ–∞–ї—М–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ. –Ґ–Њ–≥–і–∞ —Н—В–Њ –Ј–∞–і–∞—З–∞ –Э–µ–є–Љ–∞–љ–∞, –Ї–Њ—В–Њ—А–∞—П —В–∞–Ї–ґ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є –≤–љ—Г—В—А–µ–љ–љ–µ–є –Є –≤–љ–µ—И–љ–µ–є.
–Ъ—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –Є–Љ–µ–µ—В –≤–Є–і
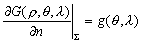
–Ф–ї—П —Б—Д–µ—А—Л –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —А–∞–≤–µ–љ—Б—В–≤–Њ
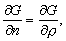 –њ–Њ—Н—В–Њ–Љ—Г –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
–њ–Њ—Н—В–Њ–Љ—Г –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М —В–∞–Ї
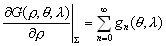 , (8.7)
, (8.7)
–≥–і–µ
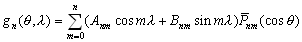 вИЪ —Д—Г–љ–Ї—Ж–Є—П –Ы–∞–њ–ї–∞—Б–∞ .
вИЪ —Д—Г–љ–Ї—Ж–Є—П –Ы–∞–њ–ї–∞—Б–∞ .
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
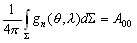 , –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П —В–µ–Њ—А–µ–Љ—Л –У–∞—Г—Б—Б–∞ –і–ї—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –Њ –њ–Њ—В–Њ–Ї–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л –≤—Л–њ–Њ–ї–љ—П–ї–Њ—Б—М —Г—Б–ї–Њ–≤–Є–µ
, –і–ї—П –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П —В–µ–Њ—А–µ–Љ—Л –У–∞—Г—Б—Б–∞ –і–ї—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –Њ –њ–Њ—В–Њ–Ї–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л –≤—Л–њ–Њ–ї–љ—П–ї–Њ—Б—М —Г—Б–ї–Њ–≤–Є–µ  , —З—В–Њ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ —Г—Б–ї–Њ–≤–Є—О
, —З—В–Њ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ —Г—Б–ї–Њ–≤–Є—О 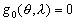 .
.
|
–Т–љ—Г—В—А–µ–љ–љ—П—П –њ—А–Њ–±–ї–µ–Љ–∞ –Э–µ–є–Љ–∞–љ–∞ |
–Т–љ–µ—И–љ—П—П –њ—А–Њ–±–ї–µ–Љ–∞ –Э–µ–є–Љ–∞–љ–∞ |
|
–Э–µ—В—А—Г–і–љ–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ —А–µ—И–µ–љ–Є–µ–Љ –≤–љ—Г—В—А–µ–љ–љ–µ–є –њ—А–Њ–±–ї–µ–Љ—Л –Э–µ–є–Љ–∞–љ–∞ –±—Г–і–µ—В |
–≠—В—Г –њ—А–Њ–±–ї–µ–Љ—Г –љ–∞ —Б—Д–µ—А–µ —А–µ—И–∞–µ—В —Д—Г–љ–Ї—Ж–Є—П |
|
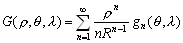 (8.8) (8.8)
|

|
|
–Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ , —Н—В–∞ —Д—Г–љ–Ї—Ж–Є—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–∞—П, —В–∞–Ї –Ї–∞–Ї —Б–Њ—Б—В–Њ–Є—В –Є–Ј —Б—Г–Љ–Љ—Л —И–∞—А–Њ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞, –∞ –њ–Њ–і—Б—В–∞–љ–Њ–≤–Ї–∞ –µвХ¶ –≤ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ (8.7) —Г–±–µ–ґ–і–∞–µ—В –љ–∞—Б —З—В–Њ –Њ–љ–Њ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П. |
–Т —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ—Б—В–Є —Н—В–Њ–≥–Њ —Г—В–≤–µ—А–ґ–і–µ–љ–Є—П –њ—А–µ–і–ї–∞–≥–∞–µ–Љ —Г–±–µ–і–Є—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. |
–°–Љ–µ—И–∞–љ–љ–∞—П –Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞
–≠—В–∞ –Ј–∞–і–∞—З–∞, –Ї–∞–Ї –Є –і–≤–µ –њ—А–µ–і—Л–і—Г—Й–Є–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Є –≤–љ—Г—В—А–µ–љ–љ—П—П, –Є –≤–љ–µ—И–љ—П—П. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –≤–∞—А–Є–∞–љ—В –≤–љ–µ—И–љ–µ–є —Б–Љ–µ—И–∞–љ–љ–Њ–є –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є, –Є–Љ–µ—О—Й–µ–є –Њ—В–љ–Њ—И–µ–љ–Є–µ –Ї —В–µ–Њ—А–Є–Є —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є. –Ъ—А–∞–µ–≤—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –±—Г–і–µ—В –ї–Є–љ–µ–є–љ–∞—П –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П —Б–∞–Љ–Њ–є –Є—Б–Ї–Њ–Љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Є –µвХ¶ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є –љ–∞ –≥—А–∞–љ–Є—З–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є
 (8.9)
(8.9)
–°–љ–Њ–≤–∞ —А–µ—И–µ–љ–Є–µ –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –≤ –≤–Є–і–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ —Д—Г–љ–Ї—Ж–Є—П–Љ
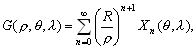
–≥–і–µ
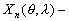 —Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, –њ–Њ–і–ї–µ–ґ–∞—Й–∞—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О. –Я–Њ–і—Б—В–∞–≤–Є–Љ —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ (8.9):
—Б—Д–µ—А–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П, –њ–Њ–і–ї–µ–ґ–∞—Й–∞—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О. –Я–Њ–і—Б—В–∞–≤–Є–Љ —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ (8.9):
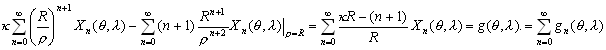
–Я—А–Є—А–∞–≤–љ–Є–≤–∞—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е —Б—В–µ–њ–µ–љ–µ–є –њ–Њ—З–ї–µ–љ–љ–Њ, –њ–Њ–ї—Г—З–Є–Љ
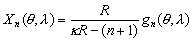
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —А–µ—И–µ–љ–Є–µ–Љ –≤–љ–µ—И–љ–µ–є —Б–Љ–µ—И–∞–љ–љ–Њ–є –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є –±—Г–і–µ—В
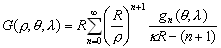 (8.10)
(8.10)
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –≤—Л—Б–Њ—В –≥–µ–Њ–Є–і–∞
–Ь—Л —Г–±–µ–і–Є–ї–Є—Б—М –≤ —В–Њ–Љ, —З—В–Њ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —П–≤–ї—П–µ—В—Б—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є –Є –љ–∞ —Б—Д–µ—А–µ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –Ї—А–∞–µ–≤–Њ–є —Г—Б–ї–Њ–≤–Є–µ (8.5) –≠—В–Њ —В–Є–њ–Є—З–љ–∞—П –≤–љ–µ—И–љ—П—П —Б–Љ–µ—И–∞–љ–љ–∞—П –Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞. –І—В–Њ–±—Л –µвХ¶ —А–µ—И–Є—В—М, –љ—Г–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М —Б–Љ–µ—И–∞–љ–љ—Г—О –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О —А—П–і–Њ–Љ –Ы–∞–њ–ї–∞—Б–∞

–≥–і–µ
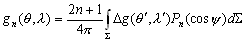 , (8.11)
, (8.11)
–≥–і–µ y
- —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г —В–Њ—З–Ї–Њ–є Q –Є —Н–ї–µ–Љ–µ–љ—В–Њ–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є dS
. –Я—А–µ–і—Б—В–∞–≤–Є–Љ —В–µ–њ–µ—А—М –њ—А–∞–≤—Г—О —З–∞—Б—В—М —Г—А–∞–≤–љ–µ–љ–Є—П (8.5), –Ј–∞–і–∞—О—Й–µ–µ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ. –Ф–ї—П –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —Б–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ
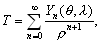
–≥–і–µ
 .
.
–Т –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ —А–µ—И–µ–љ–Є–Є –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–Є, –њ–Њ–ї—Г—З–Є–≤—И–µ–є –љ–∞–Ј–≤–∞–љ–Є–µ –Ј–∞–і–∞—З–Є –°—В–Њ–Ї—Б–∞, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ –Љ–∞—Б—Б–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ —А–∞–≤–љ–∞ –Љ–∞—Б—Б–µ —А–µ–∞–ї—М–љ–Њ–є –Ч–µ–Љ–ї–Є , —В–Њ –µ—Б—В—М
 , –∞ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б –њ–ї–∞–љ–µ—В—Л
, –∞ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Ж–µ–љ—В—А–Њ–Љ –Љ–∞—Б—Б –њ–ї–∞–љ–µ—В—Л  –Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –љ–∞—З–Є–љ–∞–µ—В—Б—П —Б –њ=2:
–Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –љ–∞—З–Є–љ–∞–µ—В—Б—П —Б –њ=2:
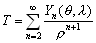 .
.
–Я—А–µ–љ–µ–±—А–µ–≥–∞—П –Ї–≤–∞–і—А–∞—В–Њ–Љ —Б–ґ–∞—В–Є—П, –Љ—Л —Б–љ–Њ–≤–∞ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є–µ –њ–Њ –љ–Њ—А–Љ–∞–ї–Є –Ј–∞–Љ–µ–љ–Є–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є—А–Њ–≤–∞–љ–Є–µ–Љ –њ–Њ —А–∞–і–Є—Г—Б-–≤–µ–Ї—В–Њ—А—Г
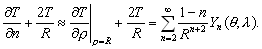
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
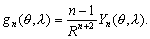
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –њ—А–Є –њ=0, –і–Њ–ї–ґ–љ–Њ –±—Л—В—М
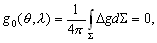
–∞ –њ—А–Є –њ=
1 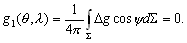
–Ш—В–∞–Ї, –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —А–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –°—В–Њ–Ї—Б–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Љ–µ—И–∞–љ–љ—Л—Е –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л—Е –∞–љ–Њ–Љ–∞–ї–Є–є —А–∞–≤–љ—П–ї–Њ—Б—М –љ—Г–ї—О –Є, –Ї—А–Њ–Љ–µ —В–Њ–≥–Њ, –і–Њ–ї–ґ–µ–љ —А–∞–≤–љ—П—В—М—Б—П –љ—Г–ї—О –Є–љ—В–µ–≥—А–∞–ї
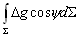 . –Ґ–µ–њ–µ—А—М —А–µ—И–µ–љ–Є–µ –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є –і–ї—П –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
. –Ґ–µ–њ–µ—А—М —А–µ—И–µ–љ–Є–µ –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є –і–ї—П –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
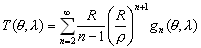 (8.12)
(8.12)
–Я–Њ–і—Б—В–∞–≤–Є–Љ —Б—О–і–∞ –Є–љ—В–µ–≥—А–∞–ї—М–љ—Г—О —Д–Њ—А–Љ—Г (8.11) –і–ї—П —Д—Г–љ–Ї—Ж–Є–є –Ы–∞–њ–ї–∞—Б–∞:
 (8.13)
(8.13)
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –≤–µ–і–µ—В—Б—П –њ–Њ —Б—Д–µ—А–µ —А–∞–і–Є—Г—Б–∞
R –≤ —Д–Њ—А–Љ—Г–ї–µ (8.13) –Љ—Л –њ–Њ–ї–∞–≥–∞–ї–Є  –Т–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ
–Т–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ
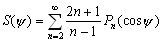 , (8.14)
, (8.14)
–Є —А–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –°—В–Њ–Ї—Б–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ—Л–є –≤–Є–і
 . (8.15)
. (8.15)
–§—Г–љ–Ї—Ж–Є—О
 —З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д—Г–љ–Ї—Ж–Є–µ–є –°—В–Њ–Ї—Б–∞. –Т (8.14) –Њ–љ–∞ –Ј–∞–і–∞–љ–∞ –≤ –≤–Є–і–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ —Б—В–µ–њ–µ–љ—П–Љ –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ –Њ—В –Ї–Њ—Б–Є–љ—Г—Б–∞ —Ж–µ–љ—В—А–∞–ї—М–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П y
. –ХвХ¶ вМ†–Ї–Њ–Љ–њ–∞–Ї—В–љ—Л–євЦ† –≤–Є–і —Б–ї–µ–і—Г—О—Й–Є–є
—З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д—Г–љ–Ї—Ж–Є–µ–є –°—В–Њ–Ї—Б–∞. –Т (8.14) –Њ–љ–∞ –Ј–∞–і–∞–љ–∞ –≤ –≤–Є–і–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ —Б—В–µ–њ–µ–љ—П–Љ –њ–Њ–ї–Є–љ–Њ–Љ–Њ–≤ –Ы–µ–ґ–∞–љ–і—А–∞ –Њ—В –Ї–Њ—Б–Є–љ—Г—Б–∞ —Ж–µ–љ—В—А–∞–ї—М–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П y
. –ХвХ¶ вМ†–Ї–Њ–Љ–њ–∞–Ї—В–љ—Л–євЦ† –≤–Є–і —Б–ї–µ–і—Г—О—Й–Є–є
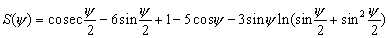
–Ы–µ–≥–Ї–Њ –≤–Є–і–µ—В—М, —З—В–Њ —В–Њ—З–Ї–∞ y
=0 - –Њ—Б–Њ–±–∞—П. –Ч–і–µ—Б—М —Д—Г–љ–Ї—Ж–Є—П –°—В–Њ–Ї—Б–∞ –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М, —В–µ–Љ –љ–µ –Љ–µ–љ–µ–µ –Є–љ—В–µ–≥—А–∞–ї (8.15) —Б—Е–Њ–і–Є—В—Б—П, –љ–Њ –њ—А–Є –≤—Л–њ–Њ–ї–љ–µ–љ–Є–Є –і–≤—Г—Е —Г–Ї–∞–Ј–∞–љ–љ—Л—Е –≤—Л—И–µ —Г—Б–ї–Њ–≤–Є–є, –Ї–Њ—В–Њ—А—Л–Љ –і–Њ–ї–ґ–љ—Л —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—В—М –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є. –Ш—Б–њ–Њ–ї—М–Ј—Г—П —Д–Њ—А–Љ—Г–ї—Г (8.1), –Ї–Њ—В–Њ—А—Г—О —З–∞—Б—В–Њ –љ–∞–Ј—Л–≤–∞—О—В —Д–Њ—А–Љ—Г–ї–Њ–є –С—А—Г–љ—Б–∞, –Є–Ј –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –ї–µ–≥–Ї–Њ –њ–Њ–ї—Г—З–Є—В—М –≤—Л—Б–Њ—В—Л –≥–µ–Њ–Є–і–∞
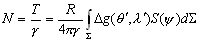 . (8.16)
. (8.16)
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Г–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–∞
–Ю—В–≤–µ—Б–љ–∞—П –ї–Є–љ–Є—П (–≤–µ—А—В–Є–Ї–∞–ї—М) —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є
g. –Ю–љ–∞ —П–≤–ї—П–µ—В—Б—П –љ–Њ—А–Љ–∞–ї—М—О –Ї —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л –љ–Њ—А–Љ–∞–ї—М –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ–Љ –≤–µ–Ї—В–Њ—А–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –≠—В–Є –і–≤–µ –љ–Њ—А–Љ–∞–ї–Є –љ–µ —Б–Њ–≤–њ–∞–і–∞—О—В. –Ь–µ–ґ–і—Г –љ–Є–Љ–Є –Њ–±—А–∞–Ј—Г–µ—В—Б—П —Г–≥–Њ–ї, –Ї–Њ—В–Њ—А—Л–є –≥–µ–Њ–і–µ–Ј–Є—Б—В—Л –љ–∞–Ј—Л–≤–∞—О—В —Г–Ї–ї–Њ–љ–µ–љ–Є–µ–Љ –Њ—В–≤–µ—Б–∞. –Э–µ –±—Г–і–µ—В –Њ—И–Є–±–Ї–Њ–є —Б–Ї–∞–Ј–∞—В—М –Є –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В–≤–µ—Б–љ–Њ–є –ї–Є–љ–Є–Є. –Я—А–∞–≤–і–∞ –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ–њ—А–Њ—Б вИЪ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В —З–µ–≥–Њ? –І—В–Њ–±—Л —В–∞–Ї–Є—Е –≤–Њ–њ—А–Њ—Б–Њ–≤ –љ–µ –≤–Њ–Ј–љ–Є–Ї–∞–ї–Њ, –Љ—Л –±—Г–і–µ–Љ —Г–њ–Њ—В—А–µ–±–ї—П—В—М –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–є —В–µ—А–Љ–Є–љ.
–Ф–≤–µ —Г–њ–Њ–Љ—П–љ—Г—В—Л–µ –љ–Њ—А–Љ–∞–ї–Є, –њ—А–Њ–і–Њ–ї–ґ–µ–љ–љ—Л–µ –≤–≤–µ—А—Е, –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П —Б –≤–Њ–Њ–±—А–∞–ґ–∞–µ–Љ–Њ–є –љ–µ–±–µ—Б–љ–Њ–є —Б—Д–µ—А–Њ–є –≤ —В–Њ—З–Ї–∞—Е, –Њ–і–љ–∞ –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –±—Г–і–µ—В –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–Љ –Ј–µ–љ–Є—В–Њ–Љ (–Є–ї–Є –њ—А–Њ—Б—В–Њ –Ј–µ–љ–Є—В–Њ–Љ), –∞ –і—А—Г–≥–∞—П вИЪ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ. –Я–Њ–љ—П—В–љ–Њ, —З—В–Њ –Є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –≥–Њ—А–Є–Ј–Њ–љ—В–∞ –∞—Б—В—А–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–≥–Њ –љ–µ —Б–Њ–≤–њ–∞–і–∞—О—В. –Ф–Њ–≥–Њ–≤–Њ—А–Є–ї–Є—Б—М —Б—З–Є—В–∞—В—М —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л–Љ, –µ—Б–ї–Є –Ј–µ–љ–Є—В —Б–Љ–µ—Й–∞–µ—В—Б—П –≤ —Б–µ–≤–µ—А–љ–Њ–Љ –Є–ї–Є –≤–Њ—Б—В–Њ—З–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є.
–Ю–±—А–∞—В–Є–Љ—Б—П –Ї –ї–Њ–Ї–∞–ї—М–љ–Њ–є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є —Б–Є—Б—В–µ–Љ–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В —Б –љ–∞—З–∞–ї–Њ–Љ –≤ –њ—Г–љ–Ї—В–µ –љ–∞–±–ї—О–і–µ–љ–Є–є (—В–Њ—З–Ї–∞ –† ). –У–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–µ –Њ—Б–Є
PX –Є PY ,–Ї–∞–Ї –Љ—Л –Ј–љ–∞–µ–Љ –Є–Ј –ї–µ–Ї—Ж–Є–Є 7, –ї–µ–ґ–∞—В –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ–є –Ї –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г. –Ю–і–љ–∞ –Є–Ј –љ–Є—Е –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –љ–∞ —Б–µ–≤–µ—А, –і—А—Г–≥–∞—П - –љ–∞ –≤–Њ—Б—В–Њ–Ї. –Ю—Б—М PZ –љ–∞–њ—А–∞–≤–ї–µ–љ–∞ –≤–љ–Є–Ј –њ–Њ –≤–љ—Г—В—А–µ–љ–љ–µ–є –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г. –Э–µ—В—А—Г–і–љ–Њ –њ–Њ–љ—П—В—М, —З—В–Њ –њ—А–Є –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ—Л—Е вМ†–≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л—ЕвЦ† –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–∞—Е –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Њ–±–µ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –±—Г–і—Г—В –Њ—В—А–Є—Ж–∞—В–µ–ї—М–љ—Л. –Я–Њ—Н—В–Њ–Љ—Г –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –≤ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –Љ–µ—А–Є–і–Є–∞–љ–∞ –Є –њ–µ—А–≤–Њ–≥–Њ –≤–µ—А—В–Є–Ї–∞–ї–∞ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Њ–њ—А–µ–і–µ–ї—П—О—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
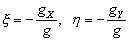 . (8.17)
. (8.17)
–Ш–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е —Д–Њ—А–Љ—Г–ї –≤–Є–і–љ–Њ, —З—В–Њ –Њ–±–µ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л - –±–µ–Ј—А–∞–Ј–Љ–µ—А–љ—Л–µ –≤–µ–ї–Є—З–Є–љ—Л, —Е–Њ—В—П –љ–∞ –њ—А–∞–Ї—В–Є–Ї–µ –Њ–љ–Є –Є–Ј–Љ–µ—А—П—О—В—Б—П –≤ —Г–≥–ї–Њ–≤—Л—Е –µ–і–Є–љ–Є—Ж–∞—Е. –Ф–µ–ї–Њ –≤ —В–Њ–Љ, —З—В–Њ —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –љ–∞ –Ч–µ–Љ–ї–µ —Б–Њ—Б—В–∞–≤–ї—П—О—В —Б–µ–Ї—Г–љ–і—Л –і—Г–≥–Є, –њ–Њ—Н—В–Њ–Љ—Г –≤–Љ–µ—Б—В–Њ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е —Д–Њ—А–Љ—Г–ї, —Б–≤—П–Ј—Л–≤–∞—О—Й–Є—Е —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ —Б –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В–∞–Љ–Є –≤–µ–Ї—В–Њ—А–∞ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –Љ—Л –≤–Ј—П–ї–Є –њ—А–Њ—Б—В–Њ–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ.
–° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л
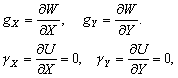
–њ–Њ—Н—В–Њ–Љ—Г
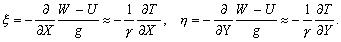 (8.19)
(8.19)
–†–∞–љ–µ–µ –Љ—Л –≤–Є–і–µ–ї–Є, —З—В–Њ
 –њ–Њ—Н—В–Њ–Љ—Г
–њ–Њ—Н—В–Њ–Љ—Г
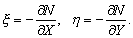 (8.20)
(8.20)
–§–Њ—А–Љ—Г–ї–∞ (8.16) –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≤—Л—З–Є—Б–ї–Є—В—М –≤—Л—Б–Њ—В—Л –≥–µ–Њ–Є–і–∞, –µ—Б–ї–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є –Ј–∞–і–∞–љ—Л —Б–Љ–µ—И–∞–љ–љ—Л–µ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є. –Я—А–Є–љ—Ж–Є–њ–Є–∞–ї—М–љ–Њ –љ–µ –Є–Љ–µ–µ—В –Ј–љ–∞—З–µ–љ–Є—П, –≤ –Ї–∞–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Ј–∞–і–∞–љ—Л —Н—В–Є –∞–љ–Њ–Љ–∞–ї–Є–Є –Є –≤ –Ї–∞–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤–µ–івХ¶—В—Б—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ. –Ь—Л –і–ї—П —Н—В–Є—Е —Ж–µ–ї–µ–є –±—Г–і–µ–Љ –њ—А–Є–Љ–µ–љ—П—В—М –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Т –Є
L. –Я–µ—А–µ–њ–Є—И–µ–Љ —Д–Њ—А–Љ—Г–ї—Г (8.16)
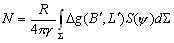
–Ш–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –±—Г–і–µ–Љ –≤—Л–њ–Њ–ї–љ—П—В—М –љ–∞ —Б—Д–µ—А–µ, –∞ –љ–µ –љ–∞ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –Я—А–Є —Н—В–Њ–Љ –Љ–Њ–ґ–љ–Њ –Њ–ґ–Є–і–∞—В—М –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—М –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–Є –≤—Л—Б–Њ—В –≥–µ–Њ–Є–і–∞ –њ–Њ—А—П–і–Ї–∞ —Б–ґ–∞—В–Є—П. –Я—А–µ–љ–µ–±—А–µ–≥–∞—П —Н—В–Є–Љ–Є –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—П–Љ–Є , –Њ–њ—А–µ–і–µ–ї–Є–Љ —Н–ї–µ–Љ–µ–љ—В–∞—А–љ—Л–µ –њ—А–Є—А–∞—Й–µ–љ–Є—П –і–ї—П –Њ—Б–µ–є
PX –Є PY
dX=RdB
dY=R cos B dL,
–њ–Њ—Н—В–Њ–Љ—Г
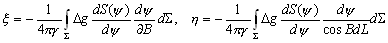 . (8.21)
. (8.21)
–Ґ–µ–њ–µ—А—М –љ—Г–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ
 . –Ф–ї—П —Н—В–Њ–≥–Њ –Њ–±—А–∞—В–Є–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–∞–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є–Є.
. –Ф–ї—П —Н—В–Њ–≥–Њ –Њ–±—А–∞—В–Є–Љ—Б—П –Ї —Д–Њ—А–Љ—Г–ї–∞–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є–Є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –Ї–Њ—В–Њ—А—Л–є –Њ–±—А–∞–Ј—Г—О—В –і—Г–≥–Є, —Б–Њ–µ–і–Є–љ—П—О—Й–Є–µ —В—А–Є —В–Њ—З–Ї–Є –љ–∞ —Б—Д–µ—А–µ: —В–Њ—З–Ї—Г –†, –≤ –Ї–Њ—В–Њ—А–Њ–є –Љ—Л —Е–Њ—В–Є–Љ –Њ–њ—А–µ–і–µ–ї–Є—В—М —Г–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В–≤–µ—Б–∞, —В–Њ—З–Ї—Г
N - –њ–Њ–ї—О—Б, –Є —В–Њ—З–Ї—Г Q вИЪ —В–µ–Ї—Г—Й—Г—О —В–Њ—З–Ї—Г –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Б—Д–µ—А—Л, –≥–і–µ —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ —Н–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є. –Ф—Г–≥–∞ PN —А–∞–≤–љ–∞ 90-–Т, –∞ –і—Г–≥–∞ QN —А–∞–≤–љ–∞ 90-–Т¢
. –£–≥–Њ–ї –њ—А–Є —В–Њ—З–Ї–µ –† —А–∞–≤–µ–љ –Р вИЪ –∞–Ј–Є–Љ—Г—В—Г —В–µ–Ї—Г—Й–µ–є —В–Њ—З–Ї–Є Q –Ф—Г–≥–∞ –†–†¢
—А–∞–≤–љ–∞ –∞—А–≥—Г–Љ–µ–љ—В—Г —Д—Г–љ–Ї—Ж–Є–Є –°—В–Њ–Ї—Б–∞ - y
. –£–≥–Њ–ї –њ—А–Є –њ–Њ–ї—О—Б–µ N —А–∞–≤–µ–љ —А–∞–Ј–љ–Њ—Б—В–Є –і–Њ–ї–≥–Њ—В —В–Њ—З–Ї–Є Q –Є —В–Њ—З–Ї–Є –†, —В–Њ –µ—Б—В—М  –Ш—Б–њ–Њ–ї—М–Ј—Г—П —Д–Њ—А–Љ—Г–ї—Л —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є–Є, –љ–µ—Б–ї–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ —Г–≥–ї–∞ y
–њ–Њ –Т –Є –њ–Њ L, –≤—Е–Њ–і—П—Й–Є–µ –≤ —Д–Њ—А–Љ—Г–ї—Л (8.21)
–Ш—Б–њ–Њ–ї—М–Ј—Г—П —Д–Њ—А–Љ—Г–ї—Л —Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є–Є, –љ–µ—Б–ї–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ —Г–≥–ї–∞ y
–њ–Њ –Т –Є –њ–Њ L, –≤—Е–Њ–і—П—Й–Є–µ –≤ —Д–Њ—А–Љ—Г–ї—Л (8.21)
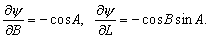
–Я–Њ–і—Б—В–∞–≤–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –≤—Л—А–∞–ґ–µ–љ–Є—П –≤ (8.21), –њ–Њ–ї—Г—З–Є–Љ
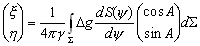
–Ч–∞–њ–Є—И–µ–Љ –њ—А–Є–≤–µ–івХ¶–љ–љ—Л–є –Є–љ—В–µ–≥—А–∞–ї –≤ –≤–Є–і–µ –і–≤—Г–Ї—А–∞—В–љ–Њ–≥–Њ –Є–љ—В–µ–≥—А–∞–ї–∞. –≠–ї–µ–Љ–µ–љ—В —Б—Д–µ—А—Л —А–∞–≤–µ–љ
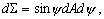 –њ—А–Є—ЗвХ¶–Љ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П y
–Є–Ј–Љ–µ–љ—П–µ—В—Б—П –Њ—В 0 –і–Њ p
, –∞ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П –Р - –Њ—В 0 –і–Њ 2p
. –Я–Њ–ї—Г—З–Є–Љ
–њ—А–Є—ЗвХ¶–Љ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П y
–Є–Ј–Љ–µ–љ—П–µ—В—Б—П –Њ—В 0 –і–Њ p
, –∞ –њ–µ—А–µ–Љ–µ–љ–љ–∞—П –Р - –Њ—В 0 –і–Њ 2p
. –Я–Њ–ї—Г—З–Є–Љ
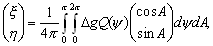
–≥–і–µ 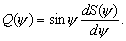 (8.22)
(8.22)
–≠—В–Є —Д–Њ—А–Љ—Г–ї—Л –љ–Њ—Б—П—В –Є–Љ—П –≥–Њ–ї–ї–∞–љ–і—Б–Ї–Њ–≥–Њ —Г—ЗвХ¶–љ–Њ–≥–Њ –Т–µ–љ–Є–љ–≥-–Ь–µ–є–љ–µ—Б–∞. –Ъ–∞–Ї –Є –≤ —Д–Њ—А–Љ—Г–ї—Г –°—В–Њ–Ї—Б–∞, –Њ–њ—А–µ–і–µ–ї—П—О—Й–µ–є –≤—Л—Б–Њ—В—Г –≥–µ–Њ–Є–і–∞ —В–Њ—З–Ї–∞ y
=0 —П–≤–ї—П–µ—В—Б—П —Г—Б—В—А–∞–љ–Є–Љ–Њ–є –Њ—Б–Њ–±–Њ–є —В–Њ—З–Ї–Њ–є.
–Э–∞ –њ—А–∞–Ї—В–Є–Ї–µ –Є—Б–њ–Њ–ї—М–Ј—Г—О—В –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–µ –Љ–µ—В–Њ–і–Є–Ї–Є –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П —Г–Ї–ї–Њ–љ–µ–љ–Є–є –Њ—В–≤–µ—Б–∞ —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –Є –≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –Є –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є—Е –і–∞–љ–љ—Л—Е.
–Ы–µ–Ї—Ж–Є—П 9
–Ю—Б–љ–Њ–≤–љ—Л–µ —В—А—Г–і–љ–Њ—Б—В–Є —А–µ—И–µ–љ–Є—П –њ—А–Њ–±–ї–µ–Љ—Л –°—В–Њ–Ї—Б–∞. –Я—А–Њ–±–ї–µ–Љ–∞ —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є –Ч–µ–Љ–ї–Є .–°–Є—Б—В–µ–Љ–∞ –≤—Л—Б–Њ—В. –У–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–∞—П, –Њ—А—В–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П –Є –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –≤—Л—Б–Њ—В—Л. –Ъ–≤–∞–Ј–Є–≥–µ–Њ–Є–і. –Р–љ–Њ–Љ–∞–ї–Є—П –≤—Л—Б–Њ—В—Л. –Ґ–µ–ї–ї—Г—А–Њ–Є–і. –Ъ—А–∞–µ–≤—Л–µ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ
.
–Ъ–≤–∞–Ј–Є–≥–µ–Њ–Є–і –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ
–Ъ—А–Є—В–Є–Ї–∞ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є —В–µ–Њ—А–Є–Є –°—В–Њ–Ї—Б–∞
–Я—А–Є–Љ–µ–љ–µ–љ–Є–µ —Д–Њ—А–Љ—Г–ї—Л –°—В–Њ–Ї—Б–∞ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤—Л—Б–Њ—В –≥–µ–Њ–Є–і–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –Њ–±—Й–µ–≥–Њ –Ј–µ–Љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞ –љ–∞—В–∞–ї–Ї–Є–≤–∞–µ—В—Б—П –љ–∞ —Б–µ—А—МвХ¶–Ј–љ—Л–µ —В—А—Г–і–љ–Њ—Б—В–Є. –Т–Њ-–њ–µ—А–≤—Л—Е, –і–ї—П –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, —З—В–Њ–±—Л –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є –±—Л–ї–Є –Є–Ј–≤–µ—Б—В–љ—Л –њ–Њ –≤—Б–µ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є, –±–Њ–ї–µ–µ –і–≤—Г—Е —В—А–µ—В–µ–є –Ї–Њ—В–Њ—А–Њ–є –њ–Њ–Ї—А—Л—В–∞ –Љ–Њ—А—П–Љ–Є –Є –Њ–Ї–µ–∞–љ–∞–Љ–Є. –Ш–Ј–Љ–µ—А–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Њ–Ї–µ–∞–љ–Њ–≤ —Б—В–∞–ї–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –ї–Є—И—М –≤ –•–• —Б—В–Њ–ї–µ—В–Є–Є.
–Т 1922-1929 –≥–Њ–і—Л –≥–Њ–ї–ї–∞–љ–і—Б–Ї–Є–є —Г—ЗвХ¶–љ—Л–є –§.–Р.–Т–µ–љ–Є–љ–≥-–Ь–µ–є–љ–µ—Б —А–∞–±–Њ—В–∞–ї –љ–∞–і —Б–Њ–Ј–і–∞–љ–Є–µ–Љ –∞–њ–њ–∞—А–∞—В—Г—А—Л –і–ї—П –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–і–≤–Є–ґ–љ–Њ–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є. –Э–∞–Ї–Њ–љ–µ—Ж, –≤ 1929 –≥–Њ–і—Г –Є–Љ –±—Л–ї —Б–Њ–Ј–і–∞–љ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ—Л–є –≤–∞—А–Є–∞–љ—В –Љ–∞—П—В–љ–Є–Ї–Њ–≤–Њ–≥–Њ –њ—А–Є–±–Њ—А–∞ —Б –Ї–Њ—В–Њ—А—Л–Љ –Т–µ–љ–Є–љ–≥-–Ь–µ–є–љ–µ—Б —Б–Њ–≤–µ—А—И–Є–ї –њ–ї–∞–≤–∞–љ–Є–µ –љ–∞ –њ–Њ–і–≤–Њ–і–љ–Њ–є –ї–Њ–і–Ї–µ –≤ –∞–Ї–≤–∞—В–Њ—А–Є—О —О–≥–Њ-–≤–Њ—Б—В–Њ—З–љ–Њ–є –Р–Ј–Є–Є, –≥–і–µ –≤ —В–Њ –≤—А–µ–Љ—П —Г –У–Њ–ї–ї–∞–љ–і–Є–Є –±—Л–ї–Є –Ї–Њ–ї–Њ–љ–Є–Є. –Ґ–Њ—З–љ–Њ—Б—В—М –≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Б—КвХ¶–Љ–Ї–Є —Г—ЗвХ¶–љ—Л–є –Њ—Ж–µ–љ–Є–ї –≤ 3 вИЪ 4 –Љ–У–∞–ї, —З—В–Њ
–±—Л–ї–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –і–ї—П –Є–Ј—Г—З–µ–љ–Є—П —Б–Њ—Б—В–Њ—П–љ–Є—П –Ј–µ–Љ–љ–Њ–є –Ї–Њ—А—Л –≤ —В–Њ–Љ —А–µ–≥–Є–Њ–љ–µ. –Э–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є —Н—В–Є—Е –і–∞–љ–љ—Л—Е –њ—А–µ–і–ї–Њ–ґ–Є–ї –љ–Њ–≤—Г—О —В–µ–Њ—А–Є—О –Є–Ј–Њ—Б—В–∞–Ј–Є–Є.
–£–ґ–µ –≤ 1930 –≥–Њ–і—Г –Ј–∞–≤–µ–і—Г—О—Й–Є–є –Ї–∞—Д–µ–і—А–Њ–є –≥—А–∞–≤–Є–Љ–µ—В—А–Є–Є –Љ–µ—Е–∞–љ–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —Д–∞–Ї—Г–ї—М—В–µ—В–∞ –Ь–У–£ –њ—А–Њ—Д–µ—Б—Б–Њ—А –Ы.–Т.–°–Њ—А–Њ–Ї–Є–љ —Б–Њ–≤–µ—А—И–Є–ї –њ–µ—А–≤–Њ–µ –њ–ї–∞–≤–∞–љ–Є–µ –≤ –І–µ—А–љ–Њ–Љ –Љ–Њ—А–µ —В–∞–Ї–ґ–µ –љ–∞ –њ–Њ–і–≤–Њ–і–љ–Њ–є –ї–Њ–і–Ї–µ —Б –Њ—А–Є–≥–Є–љ–∞–ї—М–љ–Њ–є –∞–њ–њ–∞—А–∞—В—Г—А–Њ–є, –Є–Ј–≥–Њ—В–Њ–≤–ї–µ–љ–љ–Њ–є –≤ –Љ–∞—Б—В–µ—А—Б–Ї–Є—Е –У–Р–Ш–®. –Т 1954 –≥–Њ–і—Г —Б–Є–ї–∞–Љ–Є –Є–љ—Б—В–Є—В—Г—В–∞ –Т–Э–Ш–Ш–У–µ–Њ—Д–Є–Ј–Є–Ї–∞ –±—Л–ї —Б–Њ–Ј–і–∞–љ –њ–µ—А–≤—Л–є –≤ –Љ–Є—А–µ –Љ–Њ—А—Б–Ї–Њ–є –≥—А–∞–≤–Є–Љ–µ—В—А, –∞ –≤ 1955 –≥–Њ–і—Г –њ—А–Њ—И–µ–ї –Љ–Њ—А—Б–Ї–Є–µ –Є—Б–њ—Л—В–∞–љ–Є—П –љ–∞ –њ–Њ–і–≤–Њ–і–љ–Њ–є –ї–Њ–і–Ї–µ –≤–Њ –≤—А–µ–Љ—П –њ–ї–∞–≤–∞–љ–Є—П –≤–Њ–Ї—А—Г–≥ –Э–Њ–≤–Њ–є –Ч–µ–Љ–ї–Є. –†–µ–Ј—Г–ї—М—В–∞—В—Л —Г–±–µ–і–Є—В–µ–ї—М–љ–Њ –њ–Њ–Ї–∞–Ј–∞–ї–Є, —З—В–Њ —В–Њ—З–љ–Њ—Б—В—М –≥—А–∞–≤–Є–Љ–µ—В—А–∞ –љ–µ —Г—Б—В—Г–њ–∞–µ—В —В–Њ—З–љ–Њ—Б—В–Є –Љ–∞—П—В–љ–Є–Ї–Њ–≤–Њ–≥–Њ –њ—А–Є–±–Њ—А–∞, —В—А–µ–±—Г–µ—В –≥–Њ—А–∞–Ј–і–Њ –±–Њ–ї–µ–µ –њ—А–Њ—Б—В–Њ–є –Њ–±—А–∞–±–Њ—В–Ї–Є –љ–∞–±–ї—О–і–µ–љ–Є–є. –Ь–∞—П—В–љ–Є–Ї–Њ–≤—Л–µ –њ—А–Є–±–Њ—А—Л –љ–∞–Ј–µ–Љ–љ–Њ–є –≥—А–∞–≤–Є–Љ–µ—В—А–Є–Є, –Ї–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ, –±—Л–ї–Є –≤—Л—В–µ—Б–љ–µ–љ—Л –≥—А–∞–≤–Є–Љ–µ—В—А–∞–Љ–Є, —В–Њ –ґ–µ –њ—А–Њ–Є–Ј–Њ—И–ї–Њ –Є —Б –Љ–Њ—А—Б–Ї–Є–Љ–Є –њ—А–Є–±–Њ—А–∞–Љ–Є. –Ь–Њ—А—Б–Ї–Є–µ –≥—А–∞–≤–Є–Љ–µ—В—А—Л —Б–µ–є—З–∞—Б —П–≤–ї—П—О—В—Б—П –Њ—Б–љ–Њ–≤–љ—Л–Љ–Є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–∞–Љ–Є –Љ–Њ—А—Б–Ї–Њ–є –≥—А–∞–≤–Є–Љ–µ—В—А–Є–Є. –Т—БвХ¶ –Љ–µ–љ—М—И–µ –Є –Љ–µ–љ—М—И–µ –Њ—Б—В–∞вХ¶—В—Б—П вМ†–±–µ–ї—Л—ЕвЦ† –њ—П—В–µ–љ –љ–∞ –Ч–µ–Љ–ї–µ, –≥–і–µ —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ–∞
–Т—В–Њ—А–∞—П –њ—А–Њ–±–ї–µ–Љ–∞ вИЪ –±–Њ–ї–µ–µ —Б–µ—А—МвХ¶–Ј–љ–∞—П. –Ґ–µ–Њ—А–Є—П –°—В–Њ–Ї—Б–∞ —В—А–µ–±—Г–µ—В, —З—В–Њ–±—Л –≤—Б–µ –Љ–∞—Б—Б—Л –ї–µ–ґ–∞–ї–Є –њ–Њ–і —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О, –љ–∞–Ј—Л–≤–∞–µ–Љ–Њ–є –≥–µ–Њ–Є–і–Њ–Љ. –Ъ—А–Њ–Љ–µ —В–Њ–≥–Њ, –Є–Ј–Љ–µ—А–µ–љ–Є—П —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –≤—Л–њ–Њ–ї–љ—П—О—В—Б—П –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –љ–µ —Б–Њ–≤–њ–∞–і–∞—О—Й–µ–є —Б –≥–µ–Њ–Є–і–Њ–Љ. –Ч–∞–і–∞—З–∞ —Б–Њ—Б—В–Њ–Є—В –≤ —В–Њ–Љ, —З—В–Њ–±—Л –≤ –Є–Ј–Љ–µ—А–µ–љ–љ–Њ–є –Ј–љ–∞—З–µ–љ–Є–µ –≤–љ–µ—Б—В–Є —В–∞–Ї–Є–µ –њ–Њ–њ—А–∞–≤–Ї–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Л –њ–µ—А–µ–љ–µ—Б–ї–Є –≤—Б–µ –Љ–∞—Б—Б—Л –њ–Њ–і —Г—А–Њ–≤–µ–љ—М –Љ–Њ—А—П, –љ–µ –Є–Ј–Љ–µ–љ—П—П —Б–∞–Љ–Њ–є —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –Њ–Ї–∞–Ј–∞–ї–∞—Б—М –±—Л –Њ—В–љ–µ—БвХ¶–љ–љ–Њ–є –Ї —Г—А–Њ–≤–љ—О –Љ–Њ—А—П (–≥–µ–Њ–Є–і—Г). –≠—В–∞ –њ—А–Њ–±–ї–µ–Љ–∞ —И–Є—А–Њ–Ї–Њ –Њ–±—Б—Г–ґ–і–∞–ї–∞—Б—М –≤ –љ–∞—Г—З–љ–Њ–є –ї–Є—В–µ—А–∞—В—Г—А–µ –Є –њ–Њ–ї—Г—З–Є–ї–∞ –љ–∞–Ј–≤–∞–љ–Є–µ –њ—А–Њ–±–ї–µ–Љ—Л —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є –Ч–µ–Љ–ї–Є
.
–Ю–Ї–∞–Ј–∞–ї–Њ—Б—М, —З—В–Њ –і–ї—П —Г—Б–њ–µ—И–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –њ—А–Њ–±–ї–µ–Љ—Л —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М –≤–љ—Г—В—А–µ–љ–љ–µ–µ —Б—В—А–Њ–µ–љ–Є–µ –Ч–µ–Љ–ї–Є. –Т –љ–∞—Г—З–љ—Л–є —Б–њ–Њ—А –Њ —В–Њ–Љ, –Ї–∞–Ї —А–µ—И–∞—В—М –њ—А–Њ–±–ї–µ–Љ—Г —А–µ–≥—Г–ї—П—А–Є–Ј–∞—Ж–Є–Є, –≤ 50-—Е –≥–Њ–і–∞—Е –≤–Љ–µ—И–∞–ї—Б—П –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є, –Ї–Њ—В–Њ—А—Л–є –і–Њ–Ї–∞–Ј–∞–ї, —З—В–Њ —А–∞–Ј–ї–Є—З–љ—Л–µ –≤–∞—А–Є–∞–љ—В—Л —А–µ—И–µ–љ–Є—П –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ—Л, –љ–Њ –Њ–љ–Є –љ–µ —А–µ—И–∞—О—В –Ј–∞–і–∞—З—Г –≤–њ–Њ–ї–љ–µ —Б—В—А–Њ–≥–Њ. –Ю–љ –њ—А–µ–і–ї–Њ–ґ–Є–ї —Б—В—А–Њ–≥–Њ–µ —А–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є. –Я—А–Є —Н—В–Њ–Љ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П –≤—Л—Б–Њ—В—Л –љ–µ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –Ї–Њ—В–Њ—А—Г—О –Љ—Л –љ–∞–Ј—Л–≤–∞–µ–Љ –≥–µ–Њ–Є–і–Њ–Љ, –∞ –і—А—Г–≥–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –±–ї–Є–Ј–Ї–Њ–є –Ї –≥–µ–Њ–Є–і—Г, –Ї–Њ—В–Њ—А—Г—О –Њ–љ –љ–∞–Ј–≤–∞–ї –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–Њ–Љ
–Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є —А–∞–Ј—А–∞–±–Њ—В–∞–ї —В–µ–Њ—А–Є—О –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –Ї–≤–∞–Ј–Є–µ–Њ–Є–і–∞, –њ—А–µ–і–ї–Њ–ґ–Є–ї –∞–ї–≥–Њ—А–Є—В–Љ—Л –њ—А–Є–±–ї–Є–ґвХ¶–љ–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –њ—А–Њ–±–ї–µ–Љ—Л. –Т–Њ-–њ–µ—А–≤—Л—Е, —А–µ–і—Г–Ї—Ж–Є—П (–њ–µ—А–µ–љ–Њ—Б) —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Є–ї–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –≤ –ї–Є–љ–µ–є–љ–Њ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–Є. –Т–Њ-–≤—В–Њ—А—Л—Е , —Е–Њ—В—П –≤—Б–µ –Є–Ј–Љ–µ—А–µ–љ–Є—П –Є —А–µ–і—Г–Ї—Ж–Є–Є –Њ—В–љ–Њ—Б—П—В—Б—П –Ї —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Є–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г, –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є–µ –Љ–∞–ї—Л—Е —Д—Г–љ–Ї—Ж–Є–є, –≥–і–µ —Н—В–Њ —В—А–µ–±—Г–µ—В—Б—П, –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –њ–Њ —Б—Д–µ—А–µ (—Б—Д–µ—А–Є—З–µ—Б–Ї–Њ–µ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–µ). –Ъ–Њ–љ–µ—З–љ–Њ, —В–µ–Њ—А–Є—П –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ –љ–µ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–∞—П. –Ю–љ–∞ –њ–Њ—Б—В–Њ—П–љ–љ–Њ —Б–Њ–≤–µ—А—И–µ–љ—Б—В–≤—Г–µ—В—Б—П –µ–≥–Њ —Г—З–µ–љ–Є–Ї–∞–Љ–Є. –Т –°–Њ–≤–µ—В—Б–Ї–Њ–Љ –°–Њ—О–Ј–µ –≤–Њ–Ј–љ–Є–Ї–ї–∞ —И–Ї–Њ–ї–∞ –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ, –Ї–Њ—В–Њ—А–∞—П —И–Є—А–Њ–Ї–Њ –Є–Ј–≤–µ—Б—В–љ–∞ –љ–µ —В–Њ–ї—М–Ї–Њ —Г –љ–∞—Б, –љ–Њ –Є –Ј–∞ —А—Г–±–µ–ґ–Њ–Љ.
–°–Є—Б—В–µ–Љ–∞ –≤—Л—Б–Њ—В
–Ю–њ—А–µ–і–µ–ї–Є—В—М —Д–Є–≥—Г—А—Г –Ї–∞–Ї–Њ–є-–ї–Є–±–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є вИЪ —Н—В–Њ –Ј–љ–∞—З–Є—В –Њ–њ—А–µ–і–µ–ї–Є—В—М —А–∞—Б—Б—В–Њ—П–љ–Є—П –Ї–∞–ґ–і–Њ–є —В–Њ—З–Ї–Є —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –і–Њ —В–µ–ї–∞ –Њ—В—Б—ЗвХ¶—В–∞, –Ј–∞ –Ї–Њ—В–Њ—А–Њ–µ –±–µ—АвХ¶—В—Б—П —Н–ї–ї–Є–њ—Б–Њ–Є–і –≤—А–∞—Й–µ–љ–Є—П. –≠—В–Є —А–∞—Б—Б—В–Њ—П–љ–Є—П –Њ–±—Л—З–љ–Њ –љ–∞–Ј—Л–≤–∞—О—В –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є–Љ–Є –≤—Л—Б–Њ—В–∞–Љ–Є. –Я–Њ–љ—П—В–Є–µ –≤—Л—Б–Њ—В—Л, –љ–∞ –њ–µ—А–≤—Л–є –≤–Ј–≥–ї—П–і, –љ–µ —В—А–µ–±—Г–µ—В —Г—В–Њ—З–љ–µ–љ–Є—П. –Ю–і–љ–∞–Ї–Њ —Н—В–Њ –љ–µ —В–∞–Ї. –Ь.–°.–Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є —А–∞–Ј—А–∞–±–Њ—В–∞–ї —Ж–µ–ї—Г—О —Б–Є—Б—В–µ–Љ—Г –≤—Л—Б–Њ—В –і–ї—П –≥–µ–Њ–і–µ–Ј–Є–Є.
–Ф–Њ–њ—Г—Б—В–Є–Љ, —З—В–Њ –Є–Љ–µ–µ–Љ –і–≤–µ —В–Њ—З–Ї–Є –Р –Є –Т
, –њ—А–Є—ЗвХ¶–Љ —В–Њ—З–Ї–∞ –Т –≤—Л—И–µ —В–Њ—З–Ї–Є –Р. –Х—Б–ї–Є —Б–Њ–µ–і–Є–љ–Є—В—М —Н—В–Є —В–Њ—З–Ї–Є –Ї–∞–љ–∞–ї–Њ–Љ –Є –њ—Г—Б—В–Є—В—М –≤–Њ–і—Г, –Ї—Г–і–∞ –Њ–љ–∞ –њ–Њ—В–µ—ЗвХ¶—В? –Ъ–∞–ґ–µ—В—Б—П –≤–њ–Њ–ї–љ–µ –µ—Б—В–µ—Б—В–≤–µ–љ–љ—Л–Љ –Њ—В–≤–µ—В: –Є–Ј —В–Њ—З–Ї–Є –Т –Ї —В–Њ—З–Ї–µ –Р. –Ю–і–љ–∞–Ї–Њ —Н—В–Њ –љ–µ —Б–Њ–≤—Б–µ–Љ —В–∞–Ї. –Т–µ—Б—М –≤–Њ–њ—А–Њ—Б –≤ —В–Њ–Љ, –Ї–∞–Ї –њ—А–Њ—Е–Њ–і–Є—В —Г—А–Њ–≤–µ–љ–љ–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М —З–µ—А–µ–Ј —Н—В–Є —В–Њ—З–Ї–Є. –Х—Б–ї–Є –Њ–±–µ —В–Њ—З–Ї–Є –ї–µ–ґ–∞—В –љ–∞ –Њ–і–љ–Њ–є —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, —В–Њ –≤–Њ–і–∞ –љ–Є–Ї—Г–і–∞ –љ–µ –њ–Њ—В–µ—ЗвХ¶—В. –Х—Б–ї–Є —Г—А–Њ–≤–µ–љ–љ–∞—П –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М, –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –Т –Њ–Ї–∞–ґ–µ—В—Б—П –њ–Њ–і —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О —В–Њ—З–Ї–Є –Р, —В–Њ –±—Г–і–µ—В –љ–∞–±–ї—О–і–∞—В—М—Б—П –Њ–±—А–∞—В–љ–∞—П –Ї–∞—А—В–Є–љ–∞: –≤–Њ–і–∞ –њ–Њ—В–µ—ЗвХ¶—В –Њ—В —В–Њ—З–Ї–Є –Р –Ї —В–Њ—З–Ї–µ –Т. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–ї—П –≥–Є–і—А–Њ—В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е —Б–Њ–Њ—А—Г–ґ–µ–љ–Є–є —Б–Є—Б—В–µ–Љ–∞ –≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Є—Е –≤—Л—Б–Њ—В –Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П –љ–µ–њ—А–Є–≥–Њ–і–љ–Њ–є.
–Т –≥–µ–Њ–і–µ–Ј–Є–Є –≤—Л—Б–Њ—В—Л –Њ–њ—А–µ–і–µ–ї—П—О—В –љ–Є–≤–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ–Љ. –Э–Є–≤–µ–ї–Є—А вИЪ —Н—В–Њ –Њ–њ—В–Є—З–µ—Б–Ї–∞—П —В—А—Г–±–∞, –≤–Є–Ј–Є—А–љ–∞—П –ї–Є–љ–Є—П –Ї–Њ—В–Њ—А–Њ–є —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В—Б—П —Б—В—А–Њ–≥–Њ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ —Б –њ–Њ–Љ–Њ—Й—М—О –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –≤—Л—Б–Њ–Ї–Њ —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ–≥–Њ —Г—А–Њ–≤–љ—П. –І—В–Њ–±—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ—А–µ–≤—Л—И–µ–љ–Є–µ –Њ–і–љ–Њ–є —В–Њ—З–Ї–Є –љ–∞–і –і—А—Г–≥–Њ–є, –≤ —Н—В–Є—Е —В–Њ—З–Ї–∞—Е —Г—Б—В–∞–љ–∞–≤–ї–Є–≤–∞—О—В—Б—П —Б–њ–µ—Ж–Є–∞–ї—М–љ—Л–µ –≤–µ—А—В–Є–Ї–∞–ї—М–љ—Л–µ —А–µ–є–Ї–Є. –° –њ–Њ–Љ–Њ—Й—М—О –љ–Є–≤–µ–ї–Є—А–∞ —Б –Ї–∞–ґ–і–Њ–є —А–µ–є–Ї–Є –њ–Њ–Њ—З–µ—АвХ¶–і–љ–Њ –±–µ—А—Г—В –Њ—В—Б—ЗвХ¶—В—Л, —В–Њ–≥–і–∞ —А–∞–Ј–љ–Њ—Б—В—М —Н—В–Є—Е –Њ—В—Б—ЗвХ¶—В–Њ–≤ –µ—Б—В—М –љ–Є–≤–µ–ї–Є—А–љ–Њ–µ –њ—А–µ–≤—Л—И–µ–љ–Є–µ –Њ–і–љ–Њ–є —В–Њ—З–Ї–Є –љ–∞–і –і—А—Г–≥–Њ–є.
–Э–Є–≤–µ–ї–Є—А–љ—Л–є —Е–Њ–і –Њ—В —В–Њ—З–Ї–Є –Ю , —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–љ–Њ–є, –љ–∞–њ—А–Є–Љ–µ—А, –љ–∞ —Г—А–Њ–≤–љ–µ –Љ–Њ—А—П, –Ї —В–Њ—З–Ї–µ –† –і–∞—Б—В –Є–Ј–Љ–µ—А–µ–љ–љ—Г—О –≤—Л—Б–Њ—В—Г —В–Њ—З–Ї–Є –† –љ–∞–і —Г—А–Њ–≤–љ–µ–Љ –Љ–Њ—А—П
 , –≥–і–µ D
h –љ–Є–≤–µ–ї–Є—А–љ–Њ–µ –њ—А–µ–≤—Л—И–µ–љ–Є–µ –Њ–і–љ–Њ–≥–Њ –Ј–≤–µ–љ–∞. –Х—Б–ї–Є –љ–Є–≤–µ–ї–Є—А–љ—Л–є —Е–Њ–і –Є–Љ–µ–µ—В –Љ–љ–Њ–≥–Њ –Ј–≤–µ–љ—М–µ–≤, —В–Њ —Б—Г–Љ–Љ—Г –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ–љ–Є—В—М –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ
, –≥–і–µ D
h –љ–Є–≤–µ–ї–Є—А–љ–Њ–µ –њ—А–µ–≤—Л—И–µ–љ–Є–µ –Њ–і–љ–Њ–≥–Њ –Ј–≤–µ–љ–∞. –Х—Б–ї–Є –љ–Є–≤–µ–ї–Є—А–љ—Л–є —Е–Њ–і –Є–Љ–µ–µ—В –Љ–љ–Њ–≥–Њ –Ј–≤–µ–љ—М–µ–≤, —В–Њ —Б—Г–Љ–Љ—Г –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ–љ–Є—В—М –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ .
.
–Т—Л—З–Є—Б–ї–Є–Љ —А–∞–Ј–љ–Њ—Б—В—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤ –Љ–µ–і—Г —В–Њ—З–Ї–∞–Љ–Є –Ю –Є –†
.
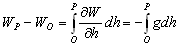 (9.1)
(9.1)
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —А–∞–Ј–љ–Њ—Б—В–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤ –љ—Г–ґ–љ–Њ –Є–Љ–µ—В—М –љ–Є–≤–µ–ї–Є—А–љ—Л–µ –њ—А–µ–≤—Л—И–µ–љ–Є—П –Є —Б–Є–ї—Г —В—П–ґ–µ—Б—В–Є –≤–і–Њ–ї—М –≤—Б–µ–≥–Њ –њ—А–Њ—Д–Є–ї—П.
–Т–≤–µ–івХ¶–Љ –≤ —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–Є–µ –µ—ЙвХ¶ –Њ–і–љ—Г —В–Њ—З–Ї—Г. –І–µ—А–µ–Ј —В–Њ—З–Ї—Г –† –њ—А–Њ—Е–Њ–і–Є—В —Б–Є–ї–Њ–≤–∞—П –ї–Є–љ–Є—П, –Ї–Њ—В–Њ—А—Г—О –Љ–Њ–ґ–љ–Њ –њ—А–Њ–і–Њ–ї–ґ–Є—В—М –і–Њ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –≥–µ–Њ–Є–і–∞ (—Г—А–Њ–≤–µ–љ—М –Љ–Њ—А—П). –Ю–љ–∞ –њ–µ—А–µ—Б–µ—ЗвХ¶—В—Б—П —Б —Н—В–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М—О –≤ —В–Њ–Ї–µ –†¢
. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ —В–Њ—З–Ї–Є –Ю –Є –†¢
–ї–µ–ґ–∞—В –љ–∞ –Њ–і–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П (–љ–∞ –≥–µ–Њ–Є–і–µ) –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —А–µ–Ј—Г–ї—М—В–∞—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —А–∞–Ј–љ–Њ—Б—В–Є –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤ –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –њ—Г—В–Є –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П, –≤—Л–±–µ—А–µ–Љ —В–∞–Ї–Њ–є –Љ–∞—А—И—А—Г—В –ЮвИЪ–†¢
вИЪ–†. –Я—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Љ—Л –њ–Њ–ї—Г—З–Є–Љ –ї–Є—И—М –љ–∞ –Њ—В—А–µ–Ј–Ї–µ —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є –†¢
-–†:  –Я—А–Є –і–≤–Є–ґ–µ–љ–Є–Є –њ–Њ —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–µ–њ—А–µ—А—Л–≤–љ–Њ –Љ–µ–љ—П–µ—В—Б—П. –°–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ –Њ —Б—А–µ–і–љ–µ–Љ, –≤ –Ї—Г—А—Б–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є —В–∞–Ї–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, –Ї–Њ—В–Њ—А–Њ–µ –Њ–љ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–љ—Г—В—А–Є –Є–љ—В–µ—А–≤–∞–ї–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П, –Ї–Њ—В–Њ—А—Л–Љ –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ–љ–Є—В—М –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ
–Я—А–Є –і–≤–Є–ґ–µ–љ–Є–Є –њ–Њ —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–µ–њ—А–µ—А—Л–≤–љ–Њ –Љ–µ–љ—П–µ—В—Б—П. –°–Њ–≥–ї–∞—Б–љ–Њ —В–µ–Њ—А–µ–Љ–µ –Њ —Б—А–µ–і–љ–µ–Љ, –≤ –Ї—Г—А—Б–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є —В–∞–Ї–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, –Ї–Њ—В–Њ—А–Њ–µ –Њ–љ–∞ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–љ—Г—В—А–Є –Є–љ—В–µ—А–≤–∞–ї–∞ –Є–љ—В–µ–≥—А–Є—А–Њ–≤–∞–љ–Є—П, –Ї–Њ—В–Њ—А—Л–Љ –Љ–Њ–ґ–љ–Њ –Ј–∞–Љ–µ–љ–Є—В—М –њ–Њ–і—Л–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ
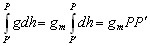
–Ю—В—А–µ–Ј–Њ–Ї —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є –†–†¢
–љ–∞–Ј—Л–≤–∞–µ—В—Б—П –Њ—А—В–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є –≤—Л—Б–Њ—В–Њ–є —В–Њ—З–Ї–Є –† –љ–∞–і —Г—А–Њ–≤–љ–µ–Љ –Љ–Њ—А—П ( —В–Њ –µ—Б—В—М –љ–∞ –≥–µ–Њ–Є–і–Њ–Љ). –Ш—В–∞–Ї
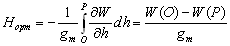 (9.2)
(9.2)
–І—В–Њ–±—Л –≤—Л—З–Є—Б–ї–Є—В—М –Њ—А—В–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї—Г—О –≤—Л—Б–Њ—В—Г, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М –љ–µ —В–Њ–ї—М–Ї–Њ –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –љ–Њ –Є —Г–Љ–µ—В—М –≤—Л—З–Є—Б–ї–Є—В—М —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –љ–∞ –Њ—В—А–µ–Ј–Ї–µ —Б–Є–ї–Њ–≤–Њ–є –ї–Є–љ–Є–Є, –∞ –і–ї—П —Н—В–Њ–≥–Њ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М –Ї–∞–Ї –Љ–µ–љ—П–µ—В—Б—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ —Н—В–Њ–Љ –Њ—В—А–µ–Ј–Ї–µ –≤–љ—Г—В—А–Є –Ч–µ–Љ–ї–Є. –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є –Ь.–°. –њ—А–µ–і–ї–Њ–ґ–Є–ї –Ј–∞–Љ–µ–љ–Є—В—М
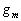 –љ–∞ —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї—М–љ–Њ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Т—Л—Б–Њ—В—Г, –Ї–Њ—В–Њ—А—Г—О –Љ—Л —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–Є–Љ –Њ–љ –љ–∞–Ј–≤–∞–ї –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є. –Ґ–∞–Ї–∞—П –Ј–∞–Љ–µ–љ–∞ –љ–µ–Є–Ј–±–µ–ґ–љ–Њ –≤–љ–µ—БвХ¶—В –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—М, –Ї–Њ—В–Њ—А–∞—П, –≤–њ—А–Њ—З–µ–Љ, –љ–µ–≤–µ–ї–Є–Ї–∞. –°–Њ–≥–ї–∞—Б–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О, –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –≤—Л—Б–Њ—В–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
–љ–∞ —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї—М–љ–Њ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є. –Т—Л—Б–Њ—В—Г, –Ї–Њ—В–Њ—А—Г—О –Љ—Л —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ –њ–Њ–ї—Г—З–Є–Љ –Њ–љ –љ–∞–Ј–≤–∞–ї –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є. –Ґ–∞–Ї–∞—П –Ј–∞–Љ–µ–љ–∞ –љ–µ–Є–Ј–±–µ–ґ–љ–Њ –≤–љ–µ—БвХ¶—В –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—М, –Ї–Њ—В–Њ—А–∞—П, –≤–њ—А–Њ—З–µ–Љ, –љ–µ–≤–µ–ї–Є–Ї–∞. –°–Њ–≥–ї–∞—Б–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О, –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –≤—Л—Б–Њ—В–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
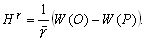 (9.3)
(9.3)
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ—А—В–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П –≤—Л—Б–Њ—В–∞ –µ—Б—В—М –≤—Л—Б–Њ—В–∞ —В–Њ—З–Ї–Є –љ–∞–і —Г—А–Њ–≤–љ–µ–Љ –Љ–Њ—А—П, —В–Њ –Љ–∞–ї–Њ –Њ—В–ї–Є—З–∞—О—Й–∞—П—Б—П –Њ—В –љ–µвХ¶ –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –≤—Л—Б–Њ—В–∞ –±—Г–і–µ—В —А–∞–≤–љ–∞ –≤—Л—Б–Њ—В–µ —В–Њ—З–Ї–Є –Њ—В –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Љ–∞–ї–Њ –Њ—В–ї–Є—З–∞—О—Й–µ–є—Б—П –Њ—В –≥–µ–Њ–Є–і–∞. –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є –љ–∞–Ј–≤–∞–ї —Н—В—Г –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В—М –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–Њ–Љ.
–Ю—В–ї–Є—З–Є–µ –Є—Б—В–Є–љ–љ–Њ–є (–≥–µ–Њ–і–µ–Ј–Є—З–µ—Б–Ї–Њ–є) –≤—Л—Б–Њ—В—Л –Њ—В –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Г–Љ–µ—Б—В–љ–Њ –љ–∞–Ј–≤–∞—В—М –∞–љ–Њ–Љ–∞–ї–Є–µ–є –≤—Л—Б–Њ—В—Л. –≠—В–Њ –њ–Њ–љ—П—В–Є–µ —В–∞–Ї–ґ–µ –≤–≤вХ¶–ї –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Є–є. –Ш—В–∞–Ї, –∞–љ–Њ–Љ–∞–ї–Є—П –≤—Л—Б–Њ—В—Л –µ—Б—В—М
 (9.4)
(9.4)
–Р–љ–Њ–Љ–∞–ї–Є—П –≤—Л—Б–Њ—В—Л –µ—Б—В—М —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–∞ –Њ—В —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞, –Є–ї–Є —А–∞–≤–љ–∞ –≤—Л—Б–Њ—В–µ –њ–Њ—З—В–Є–≥–µ–Њ–Є–і–∞. –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
 . –Т –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ –њ–Њ–љ–Є–Љ–∞–љ–Є–Є, –Њ–њ—А–µ–і–µ–ї–Є—В—М —Д–Є–≥—Г—А—Г –Ч–µ–Љ–ї–Є вИЪ —Н—В–Њ –Ј–љ–∞—З–Є—В –Њ–њ—А–µ–і–µ–ї–Є—В—М –≤—Л—Б–Њ—В—Л –≥–µ–Њ–Є–і–∞ N. –Ю–і–љ–∞–Ї–Њ, –Љ—Л –љ–µ —Б–і–µ–ї–∞–µ–Љ –±–Њ–ї—М—И–Њ–є –њ–Њ–≥—А–µ—И–љ–Њ—Б—В–Є, –µ—Б–ї–Є –±—Г–і–µ–Љ —Б—З–Є—В–∞—В—М —Д–Є–≥—Г—А–Њ–є –Ч–µ–Љ–ї–Є вИЪ —Д–Є–≥—Г—А—Г –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–∞, –∞ –і–ї—П —Н—В–Њ–≥–Њ –Љ—Л –і–Њ–ї–ґ–љ—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В.
. –Т –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–Љ –њ–Њ–љ–Є–Љ–∞–љ–Є–Є, –Њ–њ—А–µ–і–µ–ї–Є—В—М —Д–Є–≥—Г—А—Г –Ч–µ–Љ–ї–Є вИЪ —Н—В–Њ –Ј–љ–∞—З–Є—В –Њ–њ—А–µ–і–µ–ї–Є—В—М –≤—Л—Б–Њ—В—Л –≥–µ–Њ–Є–і–∞ N. –Ю–і–љ–∞–Ї–Њ, –Љ—Л –љ–µ —Б–і–µ–ї–∞–µ–Љ –±–Њ–ї—М—И–Њ–є –њ–Њ–≥—А–µ—И–љ–Њ—Б—В–Є, –µ—Б–ї–Є –±—Г–і–µ–Љ —Б—З–Є—В–∞—В—М —Д–Є–≥—Г—А–Њ–є –Ч–µ–Љ–ї–Є вИЪ —Д–Є–≥—Г—А—Г –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–∞, –∞ –і–ї—П —Н—В–Њ–≥–Њ –Љ—Л –і–Њ–ї–ґ–љ—Л –Њ–њ—А–µ–і–µ–ї–Є—В—М –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В.
–°–≤–µ–івХ¶–Љ –Ј–∞–і–∞—З—Г —Б–љ–Њ–≤–∞ –Ї –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–µ –і–ї—П –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –∞–љ–Њ–Љ–∞–ї–Є—О –≤—Л—Б–Њ—В—Л –љ—Г–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —З–µ—А–µ–Ј –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї (—Б–Љ –ї–µ–Ї—Ж–Є—О 8). –Ш—В–∞–Ї, –Є–Љ–µ–µ–Љ:
- –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –≤ —В–Њ—З–Ї–µ –† —А–∞–≤–µ–љ
 , –° вИЪ –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Њ—В —Г—А–Њ–≤–љ—П –Љ–Њ—А—П (—В–Њ—З–Ї–∞ –Ю),
–љ–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤ —В–Њ—З–Ї–µ
, –° вИЪ –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –Њ—В —Г—А–Њ–≤–љ—П –Љ–Њ—А—П (—В–Њ—З–Ї–∞ –Ю),
–љ–Њ—А–Љ–∞–ї—М–љ—Л–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї –≤ —В–Њ—З–Ї–µ 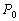 ,—А–∞–≤–љ—Л–є
,—А–∞–≤–љ—Л–є 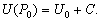
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —В–Њ—З–Ї–∞
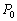 –љ–µ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —В–Њ—З–Ї–Њ–є –†, —В–∞–Ї –Ї–∞–Ї –Њ–љ–∞ –њ–Њ–і–±–Є—А–∞–µ—В—Б—П —В–∞–Ї, —З—В–Њ–±—Л –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —А–µ–∞–ї—М–љ–Њ–≥–Њ –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –±—Л–ї–Є –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–Љ–Є
–љ–µ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —В–Њ—З–Ї–Њ–є –†, —В–∞–Ї –Ї–∞–Ї –Њ–љ–∞ –њ–Њ–і–±–Є—А–∞–µ—В—Б—П —В–∞–Ї, —З—В–Њ–±—Л –њ—А–Є—А–∞—Й–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —А–µ–∞–ї—М–љ–Њ–≥–Њ –Є –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –±—Л–ї–Є –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–Љ–Є
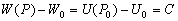 .
.
–Ч–і–µ—Б—М –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ
 –Є
–Є 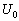 –Њ–Ј–љ–∞—З–∞—О—В —Б–ї–µ–і—Г—О—Й–µ–µ: –њ–µ—А–≤–∞—П –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ –≥–µ–Њ–Є–і–µ, –∞ –≤—В–Њ—А–∞—П вИЪ –≤–µ–ї–Є—З–Є–љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –љ–∞ —Г—А–Њ–≤–µ–љ–љ–Њ–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –Э–µ—В—А—Г–і–љ–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ –Њ—В—А–µ–Ј–Њ–Ї
–Њ–Ј–љ–∞—З–∞—О—В —Б–ї–µ–і—Г—О—Й–µ–µ: –њ–µ—А–≤–∞—П –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –µ—Б—В—М –≤–µ–ї–Є—З–Є–љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є –љ–∞ –≥–µ–Њ–Є–і–µ, –∞ –≤—В–Њ—А–∞—П вИЪ –≤–µ–ї–Є—З–Є–љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –љ–∞ —Г—А–Њ–≤–µ–љ–љ–Њ–Љ —Н–ї–ї–Є–њ—Б–Њ–Є–і–µ. –Э–µ—В—А—Г–і–љ–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ –Њ—В—А–µ–Ј–Њ–Ї  —А–∞–≤–µ–љ –∞–љ–Њ–Љ–∞–ї–Є–µ –≤—Л—Б–Њ—В—Л z
. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
—А–∞–≤–µ–љ –∞–љ–Њ–Љ–∞–ї–Є–µ –≤—Л—Б–Њ—В—Л z
. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ
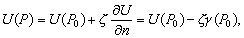
–њ–Њ—Н—В–Њ–Љ—Г
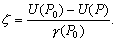
–° –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л
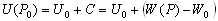 ,
,
–њ–Њ—Н—В–Њ–Љ—Г
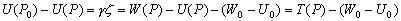
–Ю—В—Б—О–і–∞ —Б–ї–µ–і—Г–µ—В
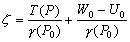 . (9.5)
. (9.5)
–Ь—Л –њ–Њ–ї—Г—З–Є–ї–Є –≤–љ–Њ–≤—М —Д–Њ—А–Љ—Г–ї—Г –С—А—Г–љ—Б–∞, –Њ–і–љ–∞–Ї–Њ –Њ–љ–∞ –Њ—В–ї–Є—З–∞–µ—В—Б—П —В–µ–Љ, —З—В–Њ —Б–Њ–і–µ—А–ґ–Є—В –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–є —З–ї–µ–љ
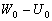 , –Ї–Њ—В–Њ—А—Л–є –≤ вМ†–Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–євЦ† —Д–Њ—А–Љ—Г–ї–µ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В. –Т —В–µ–Њ—А–Є–Є –°—В–Њ–Ї—Б–∞ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ –Њ–±–µ —Н—В–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ —А–∞–≤–љ—Л: –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –љ–∞ —Г—А–Њ–≤–љ–µ –Љ–Њ—А—П —А–∞–≤–µ–љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—Г —Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞.
, –Ї–Њ—В–Њ—А—Л–є –≤ вМ†–Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–євЦ† —Д–Њ—А–Љ—Г–ї–µ –Њ—В—Б—Г—В—Б—В–≤—Г–µ—В. –Т —В–µ–Њ—А–Є–Є –°—В–Њ–Ї—Б–∞ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ –Њ–±–µ —Н—В–Є –њ–Њ—Б—В–Њ—П–љ–љ—Л–µ —А–∞–≤–љ—Л: –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є –љ–∞ —Г—А–Њ–≤–љ–µ –Љ–Њ—А—П —А–∞–≤–µ–љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—Г —Г—А–Њ–≤–µ–љ–љ–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–Њ–Є–і–∞.
–Ф—А—Г–≥–Њ–µ –Њ—В–ї–Є—З–Є–µ: –љ–Њ—А–Љ–∞–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є –Ј–∞–і–∞вХ¶—В—Б—П –љ–µ –љ–∞ –≥–µ–Њ–Є–і–µ, –∞ –≤ –љ–µ–Ї–Њ—В–Њ—А–Њ–є —В–Њ—З–Ї–µ
 , –Њ—В—Б—В–Њ—П—Й–µ–є –Њ—В —В–µ–Ї—Г—Й–µ–є —В–Њ–Ї–Є –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ –≤–µ–ї–Є—З–Є–љ—Г, —А–∞–≤–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В—Л. –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –Љ–µ—Б—В–Њ –≤—Б–µ—Е —В–Њ—З–µ–Ї
, –Њ—В—Б—В–Њ—П—Й–µ–є –Њ—В —В–µ–Ї—Г—Й–µ–є —В–Њ–Ї–Є –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –љ–∞ –≤–µ–ї–Є—З–Є–љ—Г, —А–∞–≤–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В—Л. –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –Љ–µ—Б—В–Њ –≤—Б–µ—Е —В–Њ—З–µ–Ї 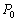 –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —В–µ–ї–ї—Г—А–Њ–Є–і–Њ–Љ. –У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є, –Ї–∞–Ї –Є –њ—А–µ–ґ–і–µ, –Њ—В–љ–Њ—Б—П—В—Б—П –Ї —А–∞–Ј–љ—Л–Љ —В–Њ—З–Ї–∞–Љ: –љ–∞–±–ї—О–і–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Ј–∞–і–∞–љ–Њ –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ вИЪ –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ.
–љ–∞–Ј—Л–≤–∞–µ—В—Б—П —В–µ–ї–ї—Г—А–Њ–Є–і–Њ–Љ. –У—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л–µ –∞–љ–Њ–Љ–∞–ї–Є–Є, –Ї–∞–Ї –Є –њ—А–µ–ґ–і–µ, –Њ—В–љ–Њ—Б—П—В—Б—П –Ї —А–∞–Ј–љ—Л–Љ —В–Њ—З–Ї–∞–Љ: –љ–∞–±–ї—О–і–µ–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –Ј–∞–і–∞–љ–Њ –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є, –∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ вИЪ –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ.
–Т –ї–Є—В–µ—А–∞—В—Г—А–µ, –њ–Њ—Б–≤—П—ЙвХ¶–љ–љ–Њ–є –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—О –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ—Л—Е –њ–Њ–ї–µ–є –њ–ї–∞–љ–µ—В, –≤—Б—В—А–µ—З–∞—О—В—Б—П –Є –і—А—Г–≥–Є–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –њ–Њ–љ—П—В–Є—П —В–µ–ї–ї—Г—А–Њ–Є–і–∞, –Ї–∞–Ї –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А—Г—О—Й—Г—О —Д–Њ—А–Љ—Г –Ч–µ–Љ–ї–Є.
–Ґ–µ–ї–ї—Г—А–Њ–Є–і –Ь–∞—А—Г—Б—Б–Є –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ. –Ґ–µ–ї–ї—Г—А–Њ–Є–і вИЪ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –Љ–µ—Б—В–Њ —В–Њ—З–µ–Ї, –≤ –Ї–Њ—В–Њ—А—Л—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї —В—П–ґ–µ—Б—В–Є —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ
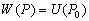 .
.
–Ґ–µ–ї–ї—Г—А–Њ–Є–і –Ъ—А–∞—А—Г–њ–∞ (–≥—А–∞–≤–Є–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —В–µ–ї–ї—Г—А–Њ–Є–і)
вИЪ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –Љ–µ—Б—В–Њ —В–Њ—З–µ–Ї, –≤ –Ї–Њ—В–Њ—А–Њ–Љ –љ–Њ—А–Љ–∞–ї—М–љ–∞—П —Б–Є–ї–∞ —В—П–ґ–µ—Б—В–Є —Б–Њ–≤–њ–∞–і–∞–µ—В —Б —Б–Є–ї–Њ–є —В—П–ґ–µ—Б—В–Є –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є 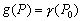 .
.
–Ъ–∞–ґ–і–Њ–µ –Є–Ј –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–є —В–µ–ї–ї—Г—А–Њ–Є–і–∞ —В—А–µ–±—Г–µ—В —Б–≤–Њ–µ–≥–Њ –њ–Њ–і—Е–Њ–і–∞ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –µ–≥–Њ —Д–Є–≥—Г—А—Л. –Ь—Л –Њ—Б—В–∞–љ–Њ–≤–Є–Љ—Б—П –Ј–і–µ—Б—М –ї–Є—И—М –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Є –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–µ –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ.
–Ъ—А–∞–µ–≤—Л–µ —Г—Б–ї–Њ–≤–Є—П –Ј–∞–і–∞—З–Є –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ
–Т —В–Њ—З–Ї–µ –† –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є –љ–∞–Љ –Є–Ј–≤–µ—Б—В–љ–Њ –Ј–љ–∞—З–µ–љ–Є–µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ —В—П–ґ–µ—Б—В–Є
W(P), –∞ –≤ —В–Њ—З–Ї–µ 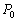 –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ - –Ј–љ–∞—З–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
–љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ - –Ј–љ–∞—З–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞  . –Ш—Б–њ–Њ–ї—М–Ј—Г—П –≤–µ–Ї—В–Њ—А–љ–Њ-–Љ–∞—В—А–Є—З–љ—Г—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї—Г –Ј–∞–њ–Є—И–µ–Љ –Њ—Б–љ–Њ–≤–љ—Л–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П, —Б–≤—П–Ј—Л–≤–∞—О—Й–Є–µ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї
. –Ш—Б–њ–Њ–ї—М–Ј—Г—П –≤–µ–Ї—В–Њ—А–љ–Њ-–Љ–∞—В—А–Є—З–љ—Г—О –Љ–∞—В–µ–Љ–∞—В–Є–Ї—Г –Ј–∞–њ–Є—И–µ–Љ –Њ—Б–љ–Њ–≤–љ—Л–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П, —Б–≤—П–Ј—Л–≤–∞—О—Й–Є–µ –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї 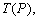 —А–∞–Ј–љ–Њ—Б—В—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤
—А–∞–Ј–љ–Њ—Б—В—М –њ–Њ—В–µ–љ—Ж–Є–∞–ї–Њ–≤  , —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –∞–љ–Њ–Љ–∞–ї–Є—О –≤—Л—Б–Њ—В—Л
, —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞, –∞–љ–Њ–Љ–∞–ї–Є—О –≤—Л—Б–Њ—В—Л –Є —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є
–Є —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є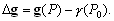
–Э–µ—В—А—Г–і–љ–Њ –≤–Є–і–µ—В—М, —З—В–Њ –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ
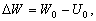 –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Ь–∞—А—Г—Б—Б–Є
–љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Ь–∞—А—Г—Б—Б–Є 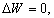 –∞ –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Ъ—А–∞—А—Г–њ–∞
–∞ –љ–∞ —В–µ–ї–ї—Г—А–Њ–Є–і–µ –Ъ—А–∞—А—Г–њ–∞ 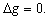 –Т –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –Є–Љ–µ–µ–Љ
–Т –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –Є–Љ–µ–µ–Љ
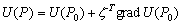 (9.6)
(9.6)
–Ґ–Њ–≥–і–∞
 ,
,
–Є–ї–Є
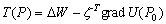 (9.7)
(9.7)
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ –њ–Њ–ї—Г—З–Є–Љ —Б–Љ–µ—И–∞–љ–љ—Г—О –∞–љ–Њ–Љ–∞–ї–Є—О
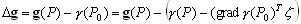 ,
,
–љ–Њ –≥—А–∞–і–Є–µ–љ—В –≤–µ–Ї—В–Њ—А–∞ g
–µ—Б—В—М –≥—А–∞–і–Є–µ–љ—В –≤—Б–µ—Е –µ–≥–Њ —Б–Њ—Б—В–∞–≤–ї—П—О—Й–Є—Е, —З—В–Њ –і–∞вХ¶—В –Љ–∞—В—А–Є—Ж—Г-—В–µ–љ–Ј–Њ—А.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ
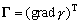
–њ–Њ—Н—В–Њ–Љ—Г
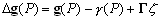 (9.8)
(9.8)
–Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ —А–∞–Ј–љ–Њ—Б—В—М
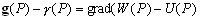 ,–µ—Б—В—М —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ–∞—П вМ†—З–Є—Б—В–∞—ПвЦ† –∞–љ–Њ–Љ–∞–ї–Є—П, —А–∞–≤–љ–∞ –≥—А–∞–і–Є–µ–љ—В—Г –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
,–µ—Б—В—М —В–∞–Ї –љ–∞–Ј—Л–≤–∞–µ–Љ–∞—П вМ†—З–Є—Б—В–∞—ПвЦ† –∞–љ–Њ–Љ–∞–ї–Є—П, —А–∞–≤–љ–∞ –≥—А–∞–і–Є–µ–љ—В—Г –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–µ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ 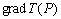 , –њ–Њ—Н—В–Њ–Љ—Г –≤–Љ–µ—Б—В–Њ (9.8) –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
, –њ–Њ—Н—В–Њ–Љ—Г –≤–Љ–µ—Б—В–Њ (9.8) –Љ–Њ–ґ–љ–Њ –Ј–∞–њ–Є—Б–∞—В—М
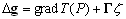 (9.9)
(9.9)
–Ш—В–∞–Ї, –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є –і–≤–∞ —Г—А–∞–≤–љ–µ–љ–Є—П, –Ї–Њ—В–Њ—А—Л–µ –љ–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є –Ч–µ–Љ–ї–Є
S –Љ–Њ–ґ–љ–Њ –≤–Ј—П—В—М –≤ –Ї–∞—З–µ—Б—В–≤–µ –Ї—А–∞–µ–≤—Л—Е —Г—Б–ї–Њ–≤–Є–є
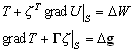
(9.10)
–Я–µ—А–≤–∞—П –Є–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е —Д–Њ—А–Љ—Г–ї –µ—Б—В—М –Њ–±–Њ–±—Й–µ–љ–Є–µ —Д–Њ—А–Љ—Г–ї—Л –С—А—Г–љ—Б–∞, —Б–≤—П–Ј—Л–≤–∞—О—Й–µ–є –≤–Њ–Ј–Љ—Г—Й–∞—О—Й–Є–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї —Б –≤—Л—Б–Њ—В–Њ–є –Ї–≤–∞–Ј–Є–≥–µ–Њ–Є–і–∞. –Ш–Ј —Н—В–Є—Е –і–≤—Г—Е —Г—А–∞–≤–љ–µ–љ–Є–є –Љ–Њ–ґ–љ–Њ –њ–Њ—Б—В—А–Њ–Є—В—М –Њ–і–љ–Њ, –µ—Б–ї–Є –Є—Б–Ї–ї—О—З–Є—В—М –∞–љ–Њ–Љ–∞–ї–Є—О –≤—Л—Б–Њ—В—Л z
. –†–µ—И–Є–Љ –≤—В–Њ—А–Њ–µ –Є–Ј –њ—А–Є–≤–µ–івХ¶–љ–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є. –Я—А–µ–і–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –Љ–∞—В—А–Є—Ж–∞ –У –љ–µ–Њ—Б–Њ–±–∞—П, –њ–Њ–ї—Г—З–Є–Љ
 . –Я–Њ–і—Б—В–∞–≤–Є–Љ –љ–∞–є–і–µ–љ–љ–Њ–µ —А–µ—И–µ–љ–Є–µ –≤ –њ–µ—А–≤–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ. –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
. –Я–Њ–і—Б—В–∞–≤–Є–Љ –љ–∞–є–і–µ–љ–љ–Њ–µ —А–µ—И–µ–љ–Є–µ –≤ –њ–µ—А–≤–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ. –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ
 (9.11)
(9.11)
–Я–Њ–і—Б—В–∞–≤–ї—П—П –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –њ–µ—А–≤–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Ј (9.10), –±—Г–і–µ–Љ –Є–Љ–µ—В—М

–Ф–ї—П —Г–њ—А–Њ—Й–µ–љ–Є—П –Ј–∞–њ–Є—Б–Є, –≤–≤–µ–івХ¶–Љ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ
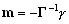 (9.12)
(9.12)
–Ґ–µ–њ–µ—А—М –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Њ–±–Њ–±—ЙвХ¶–љ–љ–Њ–є –Ј–∞–і–∞—З–Є –Ь–Њ–ї–Њ–і–µ–љ—Б–Ї–Њ–≥–Њ –њ—А–Є–љ–Є–Љ–∞–µ—В –≤–Є–і
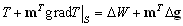 (9.13)
(9.13)
–І–∞—Б—В–љ—Л–є —Б–ї—Г—З–∞–є: –Є–Ј–Љ–µ—А–µ–љ–Є—П –≤—Л–њ–Њ–ї–љ–µ–љ—Л –љ–∞ —Г—А–Њ–≤–µ–љ–љ–Њ–є –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Б–ї—Г—З–∞–є, –Ї–Њ–≥–і–∞ –∞–љ–Њ–Љ–∞–ї–Є—П –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ вИЪ –њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞. –Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є —В–Њ—З–Ї–∞ –†, –Ї–∞–Ї –Є –≤ –Ј–∞–і–∞—З–µ –°—В–Њ–Ї—Б–∞, –љ–∞—Е–Њ–і–Є—В—Б—П –љ–∞ –њ–Њ–≤–µ—А—Е–љ–Њ—Б—В–Є —Г—А–Њ–≤–љ—П . –Ґ–Њ–≥–і–∞
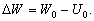 –Т—Л–±–µ—А–µ–Љ –ї–Њ–Ї–∞–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г –Њ—В—Б—ЗвХ¶—В–∞ —Б –љ–∞—З–∞–ї–Њ–Љ –≤ —В–Њ—З–Ї–µ
–Т—Л–±–µ—А–µ–Љ –ї–Њ–Ї–∞–ї—М–љ—Г—О —Б–Є—Б—В–µ–Љ—Г –Њ—В—Б—ЗвХ¶—В–∞ —Б –љ–∞—З–∞–ї–Њ–Љ –≤ —В–Њ—З–Ї–µ 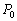 . –Ю—Б—М
. –Ю—Б—М 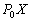 –љ–∞–њ—А–∞–≤–Є–Љ –љ–∞ —Б–µ–≤–µ—А, –Њ—Б—М
–љ–∞–њ—А–∞–≤–Є–Љ –љ–∞ —Б–µ–≤–µ—А, –Њ—Б—М 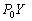 вИЪ –љ–∞ –≤–Њ—Б—В–Њ–Ї, –∞ –Њ—Б—М
вИЪ –љ–∞ –≤–Њ—Б—В–Њ–Ї, –∞ –Њ—Б—М 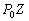 вИЪ –њ–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О –≤–љ—Г—В—А–µ–љ–љ–µ–є –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г –≤–љ–Є–Ј. –Ґ–Њ–≥–і–∞ –≤–µ–Ї—В–Њ—А –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В—Л –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ –Љ–∞—В—А–Є—Ж–µ–є-—Б—В—А–Њ–Ї–Њ–є
вИЪ –њ–Њ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О –≤–љ—Г—В—А–µ–љ–љ–µ–є –љ–Њ—А–Љ–∞–ї–Є –Ї —Н–ї–ї–Є–њ—Б–Њ–Є–і—Г –≤–љ–Є–Ј. –Ґ–Њ–≥–і–∞ –≤–µ–Ї—В–Њ—А –∞–љ–Њ–Љ–∞–ї–Є–Є –≤—Л—Б–Њ—В—Л –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–њ—А–µ–і–µ–ї–µ–љ –Љ–∞—В—А–Є—Ж–µ–є-—Б—В—А–Њ–Ї–Њ–є
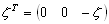
–У—А–∞–і–Є–µ–љ—В—Л –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞ –≤ —В–Њ—З–Ї–∞—Е –† –Є
 —А–∞–≤–љ—Л
—А–∞–≤–љ—Л

–Ь–∞—В—А–Є—Ж–∞ –≤—В–Њ—А—Л—Е –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞
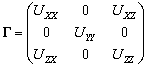
–Я–µ—А–≤–Њ–µ –Є–Ј —Г—А–∞–≤–љ–µ–љ–Є–є (9.10) –і–ї—П –Ї—А–∞–µ–≤—Л—Е —Г—Б–ї–Њ–≤–Є–є –і–∞вХ¶—В
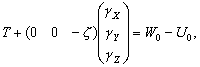
—В–Њ –µ—Б—В—М
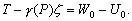
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ,
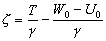 (9.14)
(9.14)
–Т—В–Њ—А–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Ј (9.10) –≤—Л–≥–ї—П–і–Є—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ
 (9.15)
(9.15)
–Я–µ—А–≤—Л–µ –і–≤–∞ —Г—А–∞–≤–љ–µ–љ–Є—П –і–∞—О—В —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞
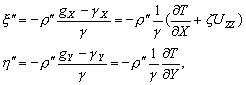 (9.17)
(9.17)
–≥–і–µ r
²
=206265 вИЪ —З–Є—Б–ї–Њ —Б–µ–Ї—Г–љ–і –≤ —А–∞–і–Є–∞–љ–µ. –Я–Њ—Б–ї–µ–і–љ–Є–є —З–ї–µ–љ –≤ —Б–Ї–Њ–±–Ї–∞—Е —Д–Њ—А–Љ—Г–ї (9.17) –і–∞вХ¶—В –Њ—З–µ–љ—М –Љ–∞–ї—Л–є –≤–Ї–ї–∞–і –Є –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ—В–±—А–Њ—И–µ–љ. –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ. –Љ—Л –≤–Є–і–µ–ї–Є, —З—В–Њ –і–ї—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–є —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ–Њ–≥–Њ –≥—А–∞–і–Є–µ–љ—В–∞ —А–∞–≤–љ–Њ 0,000811 –Љ–У–∞–ї
/–Љ . –Я—А–Є z
=100–Љ, —З—В–Њ –±—Л–≤–∞–µ—В –Њ—З–µ–љ—М —А–µ–і–Ї–Њ, –≤–µ–ї–Є—З–Є–љ–∞ 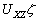 —Б–Њ—Б—В–∞–≤–Є—В 0,081 –Љ–У–∞–ї.–Є –≤–љ–µ—БвХ¶—В –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—М –≤ —Г–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В–≤–µ—Б–∞ 0,017²
, —В–Њ–≥–і–∞ –Ї–∞–Ї —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –і–Њ—Б—В–Є–≥–∞—О—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б–µ–Ї—Г–љ–і –і—Г–≥–Є.
—Б–Њ—Б—В–∞–≤–Є—В 0,081 –Љ–У–∞–ї.–Є –≤–љ–µ—БвХ¶—В –њ–Њ–≥—А–µ—И–љ–Њ—Б—В—М –≤ —Г–Ї–ї–Њ–љ–µ–љ–Є–µ –Њ—В–≤–µ—Б–∞ 0,017²
, —В–Њ–≥–і–∞ –Ї–∞–Ї —Г–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В–≤–µ—Б–∞ –і–Њ—Б—В–Є–≥–∞—О—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б–µ–Ї—Г–љ–і –і—Г–≥–Є.
–Ґ—А–µ—В—М–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Љ–µ–µ—В –≤–Є–і
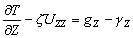 .–Я–Њ–і—Б—В–∞–≤–Є–≤ —Б—О–і–∞ –≤–µ–ї–Є—З–Є–љ—Г z
–Є–Ј (9.14) –њ–Њ–ї—Г—З–Є–Љ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –і–ї—П —Б–Љ–µ—И–∞–љ–љ—Л—Е –∞–љ–Њ–Љ–∞–ї–Є–є
.–Я–Њ–і—Б—В–∞–≤–Є–≤ —Б—О–і–∞ –≤–µ–ї–Є—З–Є–љ—Г z
–Є–Ј (9.14) –њ–Њ–ї—Г—З–Є–Љ –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –і–ї—П —Б–Љ–µ—И–∞–љ–љ—Л—Е –∞–љ–Њ–Љ–∞–ї–Є–є
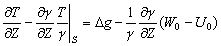 (9.18)
(9.18)
–Ь—Л –њ–Њ–ї—Г—З–Є–ї–Є, —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Ї—А–∞–µ–≤–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –њ–Њ—З—В–Є —Б–Њ–≤–њ–∞–і–∞—О—Й–µ–µ —Б –Ї—А–∞–µ–≤—Л–Љ —Г—Б–ї–Њ–≤–Є–µ–Љ –°—В–Њ–Ї—Б–∞.
–Ч–∞–і–∞—З–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Ч–µ–Љ–ї–Є —Б–≤–Њ–і–Є—В—Б—П –Ї –њ–Њ—Б—В—А–Њ–µ–љ–Є—О —А–µ—И–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞, –Ї–Њ—В–Њ—А–Њ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В –Ї—А–∞–µ–≤–Њ–Љ—Г —Г—Б–ї–Њ–≤–Є—О (9.18) –Є–ї–Є, –≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ, —Г—Б–ї–Њ–≤–Є—О (9.13). –°–њ–Њ—Б–Њ–±—Л —А–µ—И–µ–љ–Є—П —Н—В–Њ–є –Ј–∞–і–∞—З–Є –Ј–∞—Б–ї—Г–ґ–Є–≤–∞—О—В —Б–њ–µ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ –Є–Ј—Г—З–µ–љ–Є—П, –љ–Њ –≤—Л—Е–Њ–і—П—В –Ј–∞ –њ—А–µ–і–µ–ї—Л –љ–∞—И–µ–≥–Њ –Ї—Г—А—Б–∞.


Copyright (c) "–†—Г—Б—Б–Ї–Є–є –њ–µ—А–µ–њ–ї–µ—В"










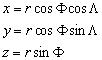 (1)
(1)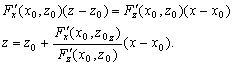 (3)
(3)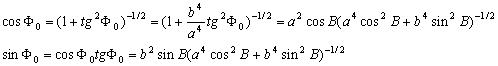
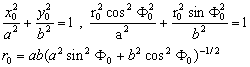 (5)
(5)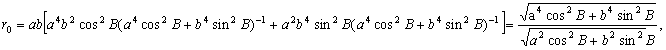
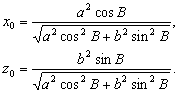 (6)
(6)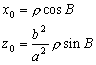 (8)
(8)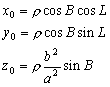 (9)
(9)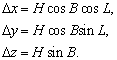 (10)
(10)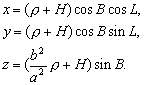 (11)
(11)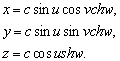
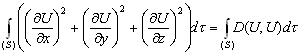 (3.4)
(3.4) (3.10)
(3.10)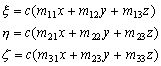
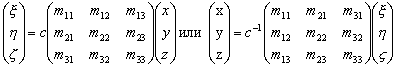
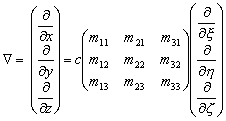
 ,
,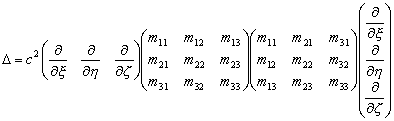
 (3.12)
(3.12)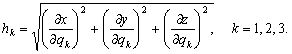


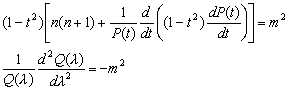 (3.21)
(3.21)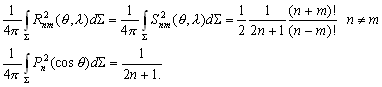 (4.9)
(4.9) 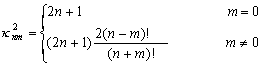
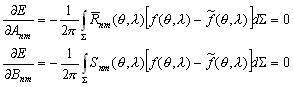 (4.15)
(4.15)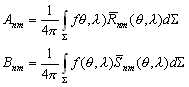 (4.16)
(4.16)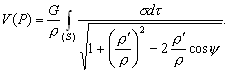
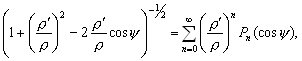
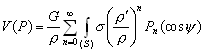 (5.2)
(5.2)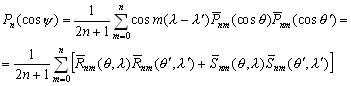
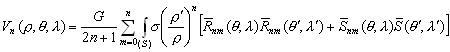 . (5.6)
. (5.6)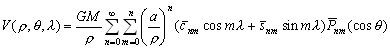 (5.9)
(5.9)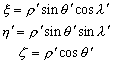 (5.14)
(5.14)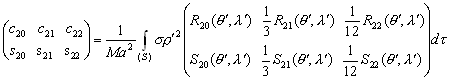
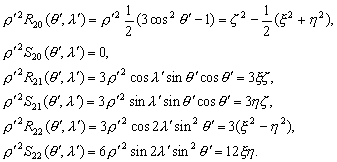 (5.17)
(5.17)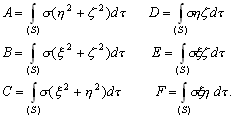 (5.18)
(5.18)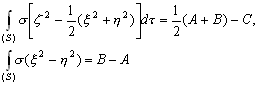
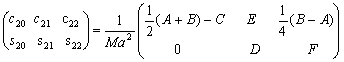 (5.19)
(5.19)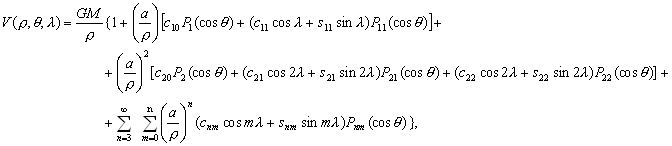
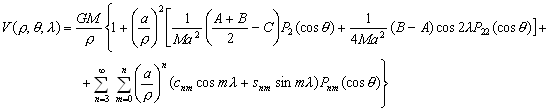 (5.21)
(5.21)  , (5.22)
, (5.22)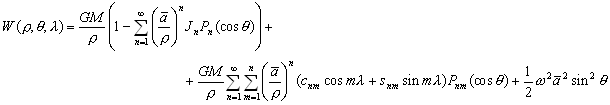 (6.1)
(6.1)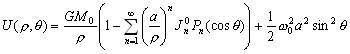 (6.2)
(6.2)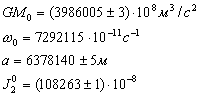
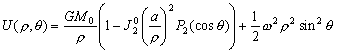 (6.3)
(6.3)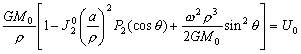 (6.4)
(6.4)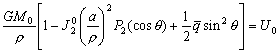 .
.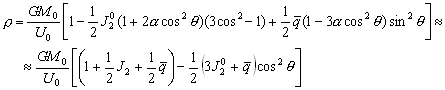
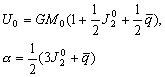 (6.6)
(6.6)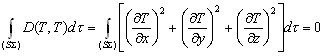
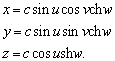
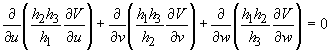 ,
,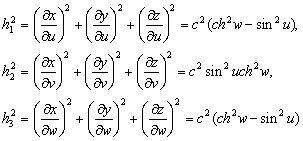 (6.8)
(6.8)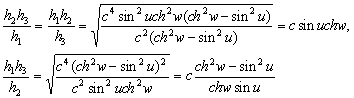 (6.9)
(6.9)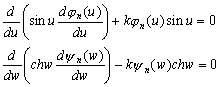 (6.13)
(6.13)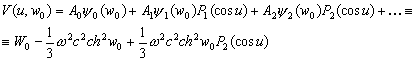 (6.17)
(6.17) (6.18)
(6.18) (6.20)
(6.20) 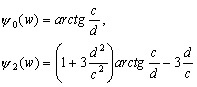 (6.21)
(6.21)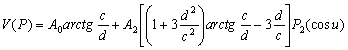 (6.22)
(6.22)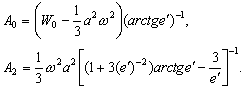 (6.23)
(6.23)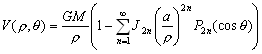 . (6.24)
. (6.24)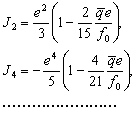
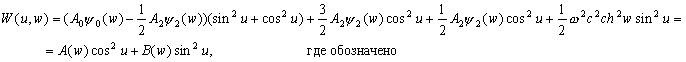

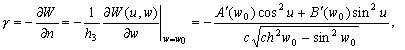

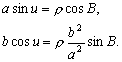

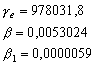
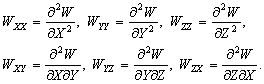
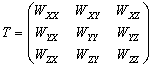 . –Я–Њ–ї—Г—З–µ–љ–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Љ–µ–µ—В 9 —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –љ–Њ –љ–µ –≤—Б–µ –Њ–љ–Є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ
. –Я–Њ–ї—Г—З–µ–љ–љ–∞—П –Љ–∞—В—А–Є—Ж–∞ –Є–Љ–µ–µ—В 9 —Н–ї–µ–Љ–µ–љ—В–Њ–≤, –љ–Њ –љ–µ –≤—Б–µ –Њ–љ–Є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л. –°–Њ–≤–µ—А—И–µ–љ–љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ, —З—В–Њ 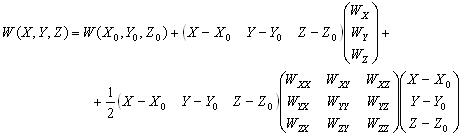 (7.7)
(7.7)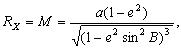
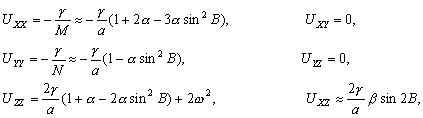 (7.14)
(7.14) (7.15)
(7.15)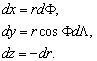 (7.17)
(7.17)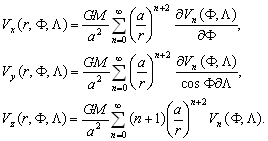 (7.20)
(7.20)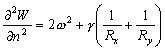 .
.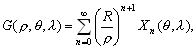
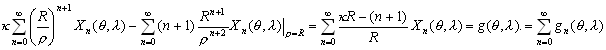
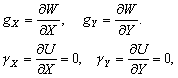
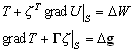
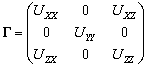
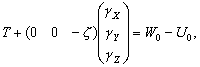
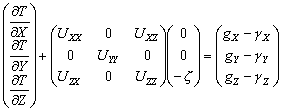 (9.15)
(9.15)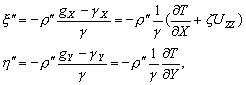 (9.17)
(9.17)